
РГР / metodicheskie_ukazaniya_zadaniya_dlya_individualnoy_raboty
.pdf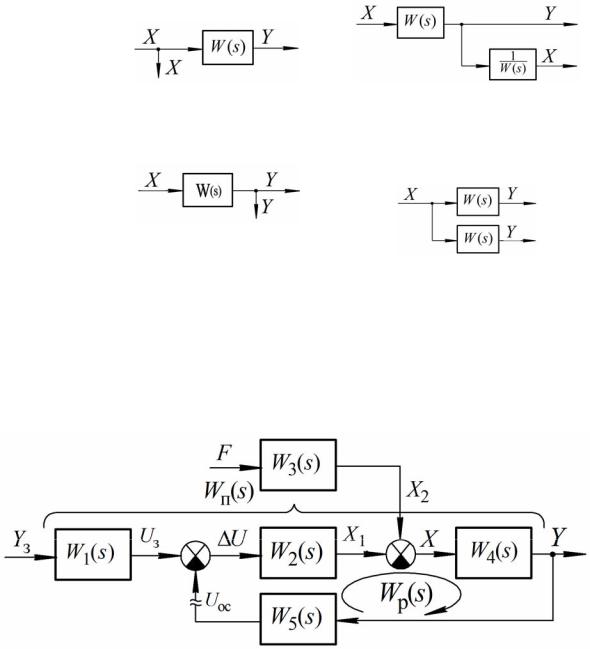
5. Перенос узла |
|
|
|
разветвления |
|
|
|
через звено |
Y =W(s)X |
X = X |
|
вперед |
|||
X = X |
Y =W(s)X |
||
|
|||
|
|
|
|
6. Перенос узла |
|
|
|
разветвления |
|
|
|
через звено |
|
|
|
назад |
Y =W(s)X |
Y =W(s)X |
|
|
|
|
Пользуясь полученными правилами структурных преобразований, произвольные структурные схемы реальных замкнутых САУ можно преобразовать к одноконтурному виду, приведенному на рис. 2.6.
Рис. 2.6. Обобщенная структура замкнутой САУ На основе схемы можем записать основные передаточные функции
САУ, которые устанавливают связь управляемой величины со входными воздействиями:
|
YY |
(s) |
|
W (s) |
|
|
|
|
|
|
|
з |
|
= |
п |
|
=W (s) |
. |
(2.10) |
|
|
|
|
|
|
||||
|
|
Yз(s) 1+Wр(s) |
Y,Yз |
||||||
|
|
|
|
|
|||||
Величину |
WY,Y (s) |
называют |
передаточной функцией |
замкнутой |
|||||
|
з |
|
|
|
|
|
|
|
|
системы по задающему воздействию.
Аналогичным образом полученную величину
21
YF (s) |
= |
W3 (s)W4 (s) |
=W |
(s) |
(2.11) |
|
|
||||
F(s) 1+WР (s) |
Y ,F |
|
|||
|
|
|
|||
называют передаточной функцией замкнутой системы по возмущающему воздействию.
К основным передаточным функциям замкнутых САУ относят также функции, устанавливающие связь сигнала рассогласования U (s) с
входными воздействиями. Применив общее правило, получим:
- для передаточной функции по сигналу рассогласования, вызванному задающим воздействием
W U ,Yз (s) = |
U(s) |
= |
|
W1(s) |
; |
(2.12) |
Y (s) |
|
1+W (s) |
||||
|
з |
|
|
р |
|
|
- для передаточной функции по сигналу рассогласования, вызванному возмущающим воздействием
W U,F (s) = |
U(s) |
=− |
W3(s)W4 (s)W5(s) |
, |
(2.13) |
|
F(s) |
1+Wр(s) |
|||||
|
|
|
|
|||
где Wп(s) =W1(s)W2 (s)W4 (s) - |
передаточная функция |
прямой цепи |
||||
(эквивалентная передаточная функция между точкой приложения задающего воздействия и управляемой величиной при разомкнутом контуре обратной связи); Wр(s) =W2 (s)W4 (s)W5 (s) - передаточная функция разомкнутого контура, получаемая при мысленном размыкании контура (чаще всего, на участке действия сигнала обратной связи) относительно точек размыкания, вычисленная без учета передаточной функции элемента сравнения.
Пример 2.1.
Исходное уравнение системы имеет вид:
a0 y′′(t) + a1 y′(t) + a2 y(t) = b0u′(t) + b1u(t) + c0 f (t) .
Представим это уравнение в стандартной форме.
Решение.
Имеем:
22

|
a0 |
′′ |
a1 |
′ |
|
b1 |
|
b0 |
|
′ |
|
|
c0 |
f (t) . |
||
|
a |
|
|
|
|
|
|
|||||||||
|
y (t) + a |
y (t) + y(t) = a |
b |
u (t) +u(t) |
+ a |
|
||||||||||
2 |
|
2 |
|
2 |
|
1 |
|
|
|
2 |
|
|||||
Введем обозначения: |
a0 |
a2 =T02 ; |
a1 |
a2 |
=T1 ; |
b1 |
a2 |
= k1 ; b0 b1 = T2 ; |
||||||||
c0  a2 = k2 .
a2 = k2 .
Тогда:
T02 y′′(t) +T1 y′(t) + y(t) = k1 [T2u′(t) +u(t)]+ k2 f (t) .
Коэффициенты T0 , T1 и T2 имеют размерность времени, т.к.
[T0 ]2 [y] |
|
[T1 ] [y] |
[y] [T2 ] [u] |
|
[y] |
[f ], |
|
c2 |
+ |
c |
+[y]= [u] |
c |
+[u] |
+ [f ] |
|
и называются постоянными времени. Их значения определяют скорость и характер протекания переходных процессов.
Коэффициенты k1 и k2 |
называются коэффициентами передачи, имеют |
размерность [k1]=[y] [u], |
[k2 ]=[y] [f ] и определяют взаимосвязь |
переменных в установившихся статических режимах.
Пример 2.2.
Пусть система описывается уравнением вида a 0 y ′′ + a1 y ′ + a 2 y = k x .
Требуется найти передаточную функцию W(s) системы при k = 1, a 0 = 1 , a1 = 3 , a 2 = 2 .
Решение.
Преобразуем уравнение системы по Лапласу при нулевых начальных
условиях. Получим (a0 s2 + a1s + a2 )Y (s) = kX (s) . Откуда передаточная функция будет:
W(s) = |
Y(s) |
= |
|
k |
|
= |
1 |
. |
X (s) |
a s2 |
+ a s + a |
s2 + 3s + 2 |
|||||
|
|
0 |
1 |
2 |
|
|
|
|
23

Пример 2.3.
Уравнение САУ по каналу вход-выход имеет вид:
0,0079yўўў(t) + 0,054yўў(t) + 0,3431yў(t) + y(t) = 2801,74u(t) .
Преобразовать это уравнение в уравнения состояния и решить их.
Решение.
Преобразуем (2.50) к нормированному виду:
ўўў |
ўў |
ў |
(2.14) |
y (t) + 6,84y |
(t) + 43, 43y (t) + 126,58y(t) = 354650,6u(t) . |
||
Обозначим: x1 (t) = y(t) ; x2 (t) = y′(t) ; x3 (t) = yўў(t) и преобразуем
исходное уравнение к системе вида: |
|
|
|
|
|
|
|
|
|||||||
|
|
x1′(t) = x2 (t); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2′(t) = x3 (t); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.15) |
|
|
x3′(t) = −126,58x1 (t) −43, 43x2 (t) −6,84x3 (t) +354650,6u(t); . |
|||||||||||||
|
|
y(t) = x1 (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Тогда уравнения состояния САУ принимают вид: |
|
||||||||||||
|
|
|
|
x′(t) = Ax(t) + Bu(t), |
|
|
|
|
|
|
|||||
|
|
|
|
y(t) = Cx(t) |
|
|
, |
|
|
|
|
(2.16) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
0 |
1 |
; B = |
|
354650, 6 |
|
; |
C = |
|
1 0 0 |
|
; |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
−126,58 |
−43, 43 |
−6,84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x(t) = x1(t) x2 (t) x3 (t) T .
Решение системы (2.16) удобно производить при помощи программы Simulink, воспользовавшись методом понижения порядка производных.
Соответствующая блок-схема приведена рис. 2.7.
24
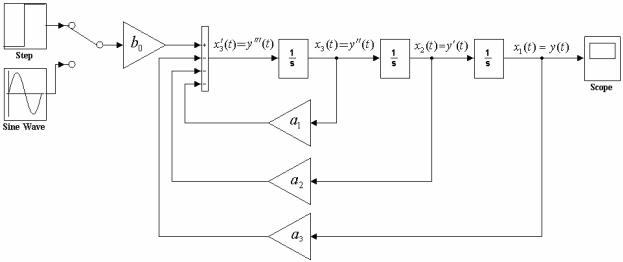
Рис. 2.7. Блок-схема решения дифференциального уравнения третьего
порядка при помощи программы Simulink
25
Контрольные вопросы
1.Какое дифференциальное уравнение называется линейным?
2.Как составляются дифференциальные уравнения элементов САУ?
3.Объясните сущность линеаризации.
4.Что называется передаточной функцией САУ или ее элемента?
5.Как определить вид передаточной функции по заданному дифференциальному уравнению?
6.Нарисуйте переходные характеристики типовых звеньев САУ.
7.Что отражает структурная схема системы управления?
8.Какие вам известны виды соединения звеньев и как определить их передаточные фикции?
9.Назовите виды передаточных функций замкнутых САУ.
10.Какие системы называются статическими и какие астатическими?
11.Как определить передаточную функцию между произвольными переменными структурной схемы САУ?
12.Как из дифференциального уравнения элемента получить его уравнение статики?
13.Как получить в общем случае из дифференциального уравнения переходную функцию?
14.Как связаны друг с другом переходная и весовая функции?
15.Как из дифференциального уравнения элемента получить его передаточную функцию?
16.Как от передаточной функции элемента перейти к его уравнению динамики в изображениях, а затем в оригиналах?
17.По каким правилам определяются эквивалентные передаточные функции для последовательного, параллельного и встречно-параллельного соединений линейных элементов? Запишите соответствующие формулы для случая двух соединенных элементов.
18.Что такое разомкнутый контур системы и чему равна его передаточная функция?
19.Как записывается в общем случае характеристическое уравнение замкнутой системы через передаточную функцию разомкнутого контура?
20.Из каких составляющих складывается сигнал ошибки в типовой системе? От каких внешних воздействий они зависят?
21.Как связаны сигнал ошибки и его составляющие с передаточной функцией разомкнутого контура?
26
3. Характеристики САУ.
Временные характеристики. Частотные характеристики.
Логарифмические частотные характеристики. Соотношения взаимосвязи
характеристик САУ между собой и передаточной функцией.
Дифференциальные уравнения не зависимо от формы представления является самой общей формой описания САУ и не дают наглядного представления о всех ее свойствах. Более наглядно характеризуют эти свойства функции y(t) , являющиеся решениями дифференциальных
уравнений. Наиболее широкое использование при описании динамических свойств получила переходная функция h(t) . Переходной функцией называют функцию, описывающую изменение выходной величины, возникающее после подачи на вход единичного ступенчатого воздействия 1(t) при
нулевых начальных условиях. График переходной функции называется
переходной характеристикой.
Второй временной характеристикой является импульсная переходная функция w(t) . Под этой функцией подразумевают функцию, описывающую изменение выходной величины, возникающее после подачи на вход дельта– функции при нулевых начальных условиях. График w(t) называют
импульсной переходной характеристикой.
Линейные САУ описываются дифференциальными уравнениями вида:
a0 y(n) (t) + a1 y(n−1) (t) + K + an y(t) = b0 x(m) (t) +b1 x(m−1) (t) + K +bm x(t) , |
(3.1) |
где x(t) и y(t) – соответственно, входная и выходная величины; ai , |
bj – |
коэффициенты; n – порядок уравнения.
Из курса высшей математики известно, что интегрирование уравнения (3.1) сводится к нахождению суммы общего решения однородного уравнения
27
без правой части yс(t) и какого–либо частного решения неоднородного
уравнения yв(t) , т.е.:
y(t) = yс(t) + yв(t) . |
(3.2) |
Изменение выходной величины, определяемое |
составляющей yс(t) |
называется свободным движением, т.к. зависит только от вида левой части уравнения (3.1), т.е. от внутренних свойств самого объекта. Составляющая yв(t) , наоборот, зависит от характера входного воздействия и поэтому
соответствующее изменение называется вынужденным движением. |
|
Составляющая yс(t) ищется в виде: |
|
yс (t ) = e pt , |
(3.3) |
где p – некоторое рациональное число. |
|
Подставив (3.3) в уравнение (3.1) при нулевой правой части, получим: |
|
a0 pnept + a1 pn−1ept + K + anept = 0 , |
|
или |
|
a0 pn + a1 pn−1 + K + an = 0 . |
(3.4) |
Последнее уравнение называется характеристическим.
Таким образом выражение (3.3) является решением исходного уравнения при условии, что p является корнем уравнения (3.4). Так как это уравнение имеет n корней, то имеем и n линейно независимых решений
yi (t) . Воспользуемся известной теоремой математики, утверждающей, что
если n линейно независимых функций yi (t) являются решениями однородного уравнения, то общее решение этого уравнения определяется выражением:
n |
n |
|
yс (t) = ∑Ci yi (t) = ∑Cie pit , |
(3.5) |
|
i=1 |
i=1 |
|
где Ci – произвольные постоянные интегрирования.
28
Применение преобразования Лапласа значительно упрощает определение временных характеристик.
Ход решения при этом следующий.
1. Преобразуем исходное уравнение (3.1) по Лапласу при нулевых начальных условиях:
a0 snY (s) + a1sn−1Y (s) + K + anY (s) = b0 sm X (s) +b1sm−1 X (s) + K +bm X (s) .(3.6)
2. Решим алгебраическое |
уравнение (3.6) |
относительно |
Y (s) при |
||||||||||||
заданном X (s) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y (s) = |
b0 sm +b1sm−1 + K |
+bm |
X (s) = |
B(s) |
X (s) . |
|
(3.7) |
||||||||
a |
0 |
s |
n |
+ a s |
n−1 |
+ K |
+ a |
n |
A(s) |
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
В случае, если изображение является дробно-рациональной функцией, |
|||||||||||||||
т.е.: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(s) = |
C(s) |
= |
c0 sl + c1sl −1 + K + cl−1s + cl |
, |
|
||||||||||
D(s) |
d0 sr + d1sr −1 + K + dr −1s + dr |
|
|
||||||||||||
причем l < r , а коэффициенты ci , d j - действительные числа, применяется формула разложения Хевисайда:
N |
|
|
|
s |
|
|
|
f (t) = ∑ |
C(s j ) |
e |
t |
|
|||
|
|
|
j |
. |
(3.8) |
||
′ |
|
||||||
j=1 |
D (s j ) |
|
|
|
|
||
|
|
|
|
|
|
|
|
где s j - простые корни уравнения D (s) = 0 ; N |
|
- число корней. |
|
||||
Частотные характеристики описывают передаточные свойства САУ в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Эти характеристики широко используются в ТАУ, так как реальные внешние воздействия могут быть представлены в виде суммы гармонических сигналов. Они определяются вынужденной составляющей решения дифференциального уравнения при подаче на вход
воздействия: |
|
x(t) = asin(ωt) . |
(3.9) |
29

При гармоническом воздействии на входе выходная величина после
окончания переходного процесса ( yc (t) = 0 ) также изменяется |
по |
t→∞ |
|
гармоническому закону, но с другой амплитудой и фазой. При этом отношение амплитуд выходной и входной величин равно модулю, а сдвиг фаз – аргументу частотной передаточной функцией W ( jω) -отношения выходной величины ко входной, преобразованных по Фурье при нулевых начальных условиях.
Кривая, которую описывает конец вектора частотной передаточной функции на комплексной плоскости при изменении частоты от 0 до ∞ называется амплитудно-фазовой частотной характеристикой (АФЧХ).
Кроме АФЧХ, являющейся самой общей частотной характеристикой, различают следующие разновидности частотных характеристик:
-амплитудная частотная характеристика (АЧХ) – график функции
A(ω) = W ( jω) ;
-фазовая частотная характеристика (ФЧХ) – график функции
ϕ(ω) = Arg W ( jω) ;
-вещественная частотная характеристика – график функции
P(ω) = Re W ( jω) ;
- мнимая частотная характеристика |
– график функции |
Q(ω) = Im W ( jω) . |
|
Исследование частотных свойств САУ значительно упрощается, если использовать частотные характеристики, построенные в логарифмическом масштабе. Такие характеристики называются логарифмическими частотными характеристиками (ЛЧХ).
Для этого прологарифмируем W ( jω) , выраженную в показательной форме:
lgW ( jω) = lg A(ω) + jϕ(ω) lg e.
30
