29. Кординаты на плоскости и в пространстве.

Геометрия, в которой основными средствами исследования служат метод координат и метод элементарной алгебры, называется аналитической. Аналитическую геометрию можно охарактеризовать, как представление точек n – мерного пространства упорядоченными системами n чисел – координатами этих точек. Например, любую точку земли можно полностью охарактеризовать долготой, широтой и высотой над уровнем моря. Хорошим примером может служить термометр. Некоторой точке прямой ставится в соответствие число 0; положительные целые числа располагаются на равных расстояниях по одну сторону, а отрицательные – по другую, а дробные числа выстраиваются между ними. В двумерном случае положение точки на плоскости может быть определено ее расстоянием до двух фиксированных прямых – осей. Прямоугольные координаты употреблялись в геометрии еще до начала нашей эры. Древний математик Аполлоний уже пользовался прямоугольными координатами. При помощи них он определял уже известные в то время кривые: параболу, гиперболу и эллипс. Впервые идея координатного метода была развита Ферма и Декартом. В их формулировках расстояния до координатных осей могли быть только положительными числами и нулем. Идея о том, что они могут быть и отрицательными принадлежит Ньютону. Лейбниц первым назвал эти расстояния координатами. Значение аналитической геометрии состоит прежде всего в том, что она установила тесную связь между алгеброй и геометрией. По учебнику Погорелова координаты заняли одно из центральных мест. Они вводятся в седьмом классе. При нахождении координат середины отрезка рассматривается два случая возможного расположения этого отрезка: отрезок АВ не параллелен оси y, то есть х₁х₂, и х₁ = х₂, то есть отрезок параллелен оси. Формулы для вычисления расстояния между точками, координаты которых известны, также рассматриваются для различных случаев расположения этих точек. Ищем расстояние между точками А₁(х₁,y₁) и А₂(х₂,y₂). Вначале рассмотрим случай когда х₁х₂ и y₁ y₂. в этом случае получаем , что расстояние между А и А₁ равно , а расстояние между А и А₂ равно . (А – точка пересечения перпендик.к осям). Тогда по теореме Пифагора получаем искомое расстояние: .

После этого рассматриваются другие возможные случаи:

1. х₁=х₂, y₁ y₂; 2)х₁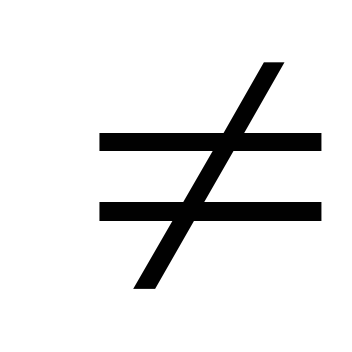х₂, y₁ = y₂; 3)х₁=х₂, y₁ = y₂; Убеждаемся, что полученная формула верна для всех этих случаев. При изучении метода координат мы выбираем обратный путь: исходя из геометрических свойств некоторых кривых выводим их уравнение. Уравнением фигуры на плоскости в декартовых координатах называется уравнение с двумя неизвестными х и y, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры. Уравнение фигуры на плоскости можно записать так: F(х,y)=0, где F(х,y) – функция двух переменных. В пространстве это уравнение примет вид: F(х,y,z)=0. В обязательную программу входят уравнения окружности и прямой. Составление уравнения окружности с центром в точке А₀(а,в) и радиусом R начинается с того, что используется геометрическое определение окружности, получаем уравнение окружности. Замечаем, что координаты х и y каждой точки А окружности удовлетворяют уравнению:

(х – а)² + (y - в)² = h². (1) Затем рассматриваем обратную задачу: покажем, что любая точка А, координаты которой удовлетворяют уравнению (1), принадлежат окружности, а это очевидно. Таким образом, мы действительно показали, что уравнение (1) есть уравнение фигуры – окружности. Вывод уравнения прямой проводится по такой же схеме.Оно имеет вид ах + вy + с = 0 В курсе геометрии рассматриваются пространственные уравнения плоскости и сферы. Уравнение плоскости имеет вид: , причем коэффициенты а, b, c являются координатами вектора, этой плоскости. Здесь учащиеся по-новому подходят к заданию прямой в пространстве. Так как любая прямая полностью определяется, если заданы две плоскости, проходящие через эту прямую, то от сюда след.что любая прямая в пространстве задается двумя линейными уравнениями – уравнениями плоскостей, проходящих через нее. Уравнение сферы вводится так же, как уравнение окружности. Следует обратить внимание на то, что основную роль в вопросах приложений метода координат занимает рациональный выбор расположения осей координат. Рассмотрим теорему: середина гипотенузы прямоугольного треугольника равно удалена от его вершин. Первым шагом при применении метода координат является такой выбор осей и начала координат, при котором алгебраические выкладки становятся более простыми. Удобнее всего вершину прямого угла расположить в начале координат.