Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ульяновский государственный педагогический университет

имени И.Н. Ульянова»

Кафедра физики

Элементарная физика

Лабораторная работа № 3

Изучение закона нормального распределения

Случайных отклонений на механической модели

Ульяновск, 2012

Цель работы: экспериментальное ознакомление с законом нормального распределения случайных величин.

Оборудование: доска Гальтона, сыпучий материал - зерна пшена, линейка.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Случайными называются события, на исход которых влияет очень большое число неподдающихся контролю факторов. К такому типу явлений, например, относятся случайные погрешности (Помимо них могут иметь место приборные и систематические погрешности.), возникающие при измерении любой физической величины. Наиболее распространенным законом распределения случайных величин является так называемый закон нормального распределения, или закон Гаусса. При нормальном распределении значения измеряемой величины сосредоточены, в основном, вблизи ее среднего значения. Отклонения от среднего в сторону больших и меньших значений (x и -x) равновероятны, причем, с ростом модуля величины отклонения от среднего эта вероятность убывает, стремясь к нулю при |x| →∞. Пусть в ΔN_x случаях из общего числа N измерений отклонение от среднего значения измеряемой величины попало в интервал от x до x+Δx. Величина ΔN_x/N называется относительной частотой (а в пределе при N→∞ вероятностью ΔP_x) того, что отклонение от среднего значения окажется в интервале от x до x+Δx. На рис. 1а по оси x отложены вправо и влево от начала отсчета (возможны положительные и отрицательные отклонения от среднего) полоски шириной Δx и высотой

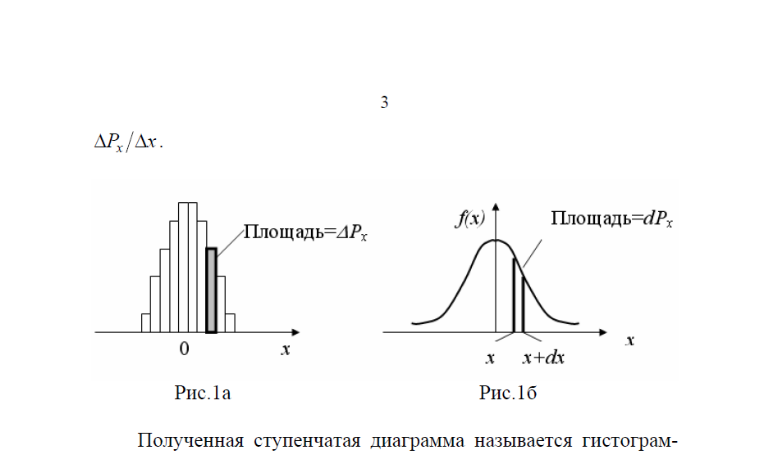
Полученная ступенчатая диаграмма называется гистограммой. Площадь полоски с координатой x равна ΔP_x, а площадь всей гистограммы – единице. Действительно:

Гистограмма наглядно характеризует вероятность получения отклонений случайной величины от ее среднего значения, заключенных в различных интервалах ширины Δx . Чем меньше ширина интервала Δx, тем детальнее будет охарактеризовано распределение вероятностей отклонений случайной величины от ее среднего значения. В пределе при Δx →0 ступенчатая линия, ограничивающая гистограмму, превратится в гладкую кривую (рис. 1б). Функция

определяющая аналитически эту кривую, называется функцией распределения вероятностей (или, для краткости, функцией распределения, законом распределения). Для нормального распределения (закон Гаусса) эта функция имеет вид:

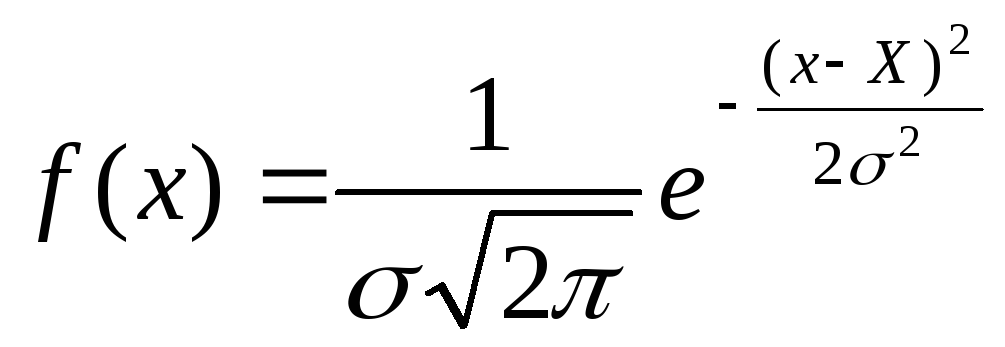(3)

Среди закономерностей в распределении случайных величин особое положение занимает нормальное (гауссово) распределение по следующим причинам. Во-первых, теория предсказывает, что распределение должно быть нормальным (гауссовым), если на результат измерения действует большое число независимых случайных факторов (как это и бывает чаще всего в физическом эксперименте). Во-вторых, при произвольной(!) функции распределения отдельного измерения, распределение средних все равно будет почти гауссовым при не слишком малом числе измерений в серии (а чаще всего и оценивают величину по среднему из нескольких измерений).

Для нормального распределения характерно, что:

- при большом числе измерений случайные погрешности одинаковой величины, но различные по знаку, встречаются одинаково часто;

- вероятность появления погрешности уменьшается с ростом величины погрешности.

Зная явный вид функции f(x), можно рассчитать вероятность того, что результат отдельного измерения попадет в любой, наперед заданный интервал значений измеряемой величины, от a до b:

(4)

Эта вероятность равна площади под графиком f(x) в пределах указанного интервала. Очевидно, вероятность того, что результат отдельного измерения попадет в интервал от -∞ до +∞ должна равняться 1, т.к. это уже есть достоверное событие:

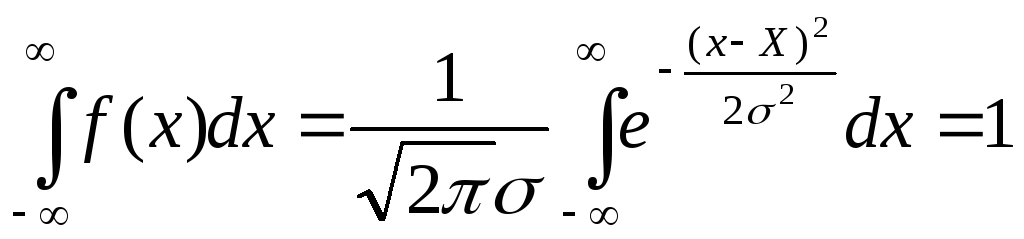(5)

Условие (5) называется условием нормировки функции f(x). Функция (3) задана двумя параметрами X и σ, смысл которых ясен из следующих расчетов:

1) Найдем среднее значение переменной x:

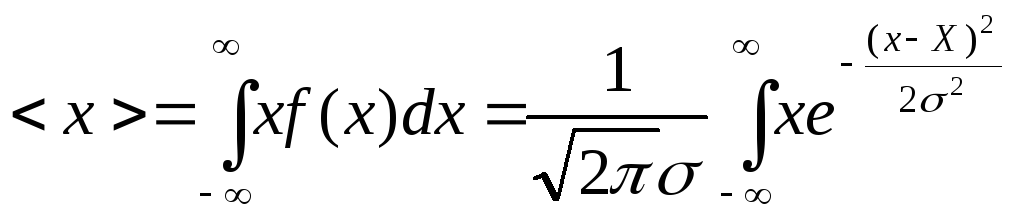
Введем новую переменную: ,. Учтем, что интеграл от нечетной функции равен нулю, а. Тогда получим:

Практическая ценность этого результата в том, что при большом числе измерений среднее значение результатов всех измерений будет мало отличаться от истинного значения измеряемой величины.

2) Найдем среднее значение квадрата погрешности (отклонения) (x-X)²:

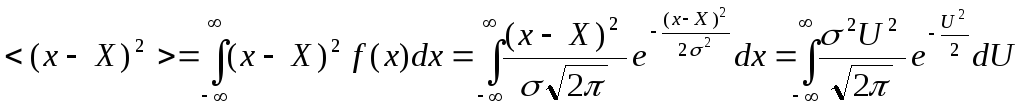
интегрируя по частям, получим:

То есть параметр есть не что иное как среднеквадратичное отклонение, которое при большом числе измерений может быть оценено по формуле:

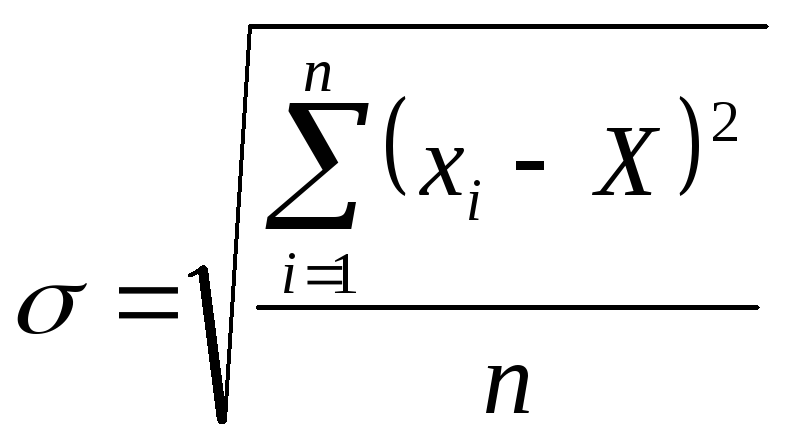(6)

Кроме того, при x = X ± σ функция (3) имеет точки перегиба см. рисунок). Докажите это самостоятельно, воспользовавшись условием, что в этих точках вторая производная функции обращается в ноль.

Найдем вероятность попадания результата единичного измерения внутрь интервала [X-σ;X+σ]:

Таким образом, параметр σ характеризует полуширину кривой гауссова распределения между точками перегиба (приблизительно на 0,6 от ее максимальной высоты), являясь мерой «расплывания» функции и, кроме того, указывает границы доверительного интервала, внутрь которого с вероятностью ≈ 68% должен попасть результат однократного измерения величины x. Величину σ называют среднеквадратичной (стандартной) погрешностью или среднеквадратичным (стандартным) отклонением.

В дальнейшем нам понадобится случай, когда <x>=X=0. Соответственно функция (3) и параметр σ запишутся следующим образом:

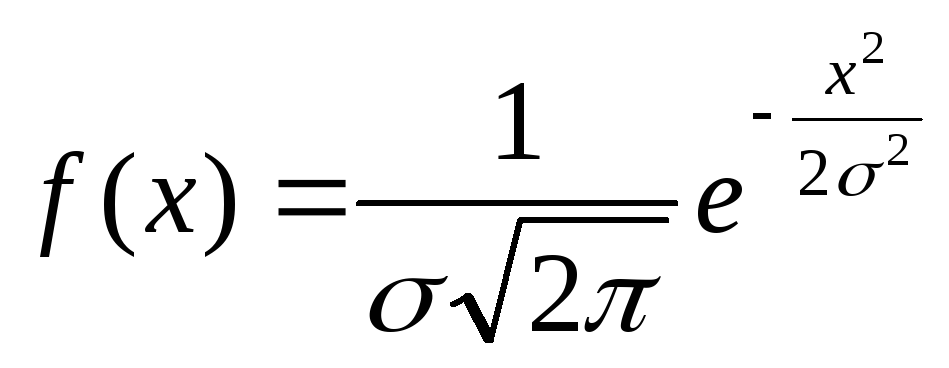(7)

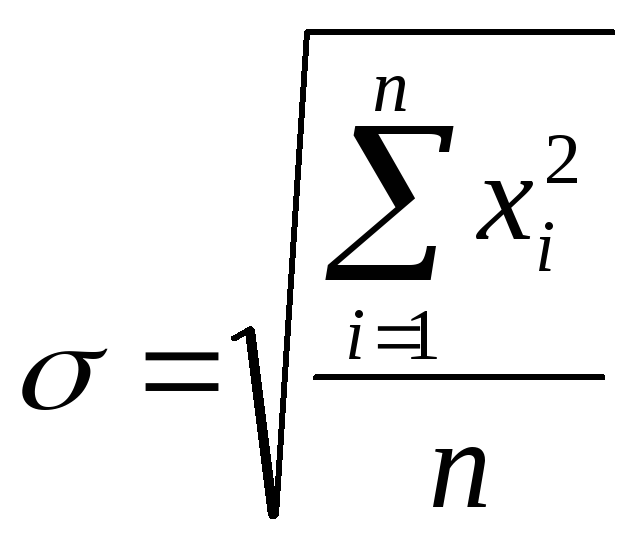(8)