19. Интеграл в школьном курсе.

К введ-ю интеграла подходят через изуч-е первообразных. Интеграл – это мн-во всех первообразных. Метод-ая схема изуч-я первообразной такова:1) рас-реть примеры взаимно обратных операций; 2) ввести интегр-ние как опер-ю, обратную диф-нию, а первообразную как рез-т опер-и интегр-ния; 3) выполнить упражнения типа: «Док-ть, что данная ф-ция F(х) есть первообразная др. данной ф-ции f(x)», «Решить з-чи на отыскание первообразной для данной ф-ции f(х)»; 4) ознакомить уч-ся с осн. св-вом первообразной и составить таблицу первообразных; 6) ознакомить уч-ся с пр-лами нахождения первообразных; 7) решить физ. з-чи с применением первообразной.

В учебнике Башмакова ввод-ся и понятия интеграл и опред-й интеграл. Подходы к введению: 1)через суммы Дарбу (число разделяющее суммы ) 2) геом-й подход (площадь криволин. трапеции) 3) интегральные суммы. В школе исп. 2): площадь криволин. трапеции – есть опред-й интеграл. Изуч-ся в очень малом объеье, как приложение для выч-я площадей фигур.

Интеграл-это понятие связано с понятием первообразной. .Сущ.три подхода введения опред.интеграла.1.через понятие сумм Дарбу .I-число,разделяющее сумму,принято считать опред.интеграл.В школе этот метод не реализуется,хотя в настоящее время есть попытки.2.понятие вводится через площадь криволинейной трапеции 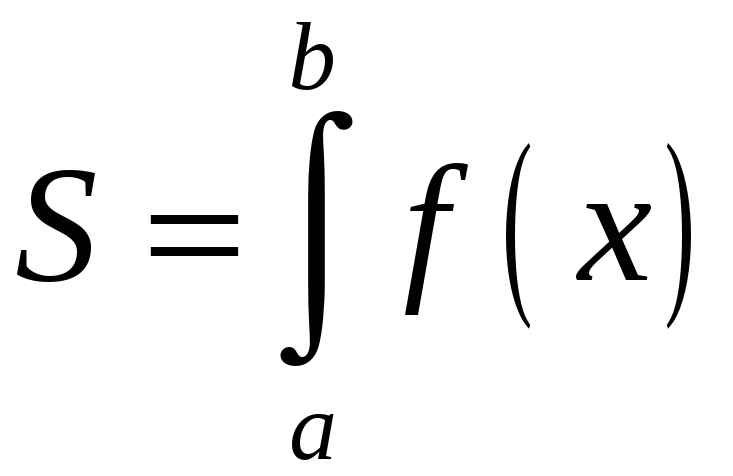.В школе введение понятия интеграла приближенно к этому методу.3.Вводится через интегральные суммы.Важным шагом является введение понятия интеграла.Возможная методическая схема введения понятия:1)привести подводящие задачи2)сформулировать опред.интеграла.Введение понятия интеграла целесообразно начать с рассм.задач,подвод.к этому понятию.Задача1.На отрезке задана непрер.и неотриц.ф-ция .Укажите новый способ нахождения площади S криволин. трапеции, образов. графиком этой ф-ции и прямыми и .В решении задачи выделим два этапа:1.построение ступенчатой фигуры и вычисление ее площади.Для этого отрезок разбиваем на n равных частей. -длина отрезка.На отрезке построим прямоугол.с высотой,аналогично на остальных отрезках.Объедин.этих прямоуг. Образует «ступенчатую» фигуру,площадь равна 2.Выражение площади S кривол.трапеции через .Делая аналогично,сравниваем ,получаем чем меньше ,т.е.чем больше n,тем меньше отличается от S.Поэтому можно предположить что площадь кривол.трапеции равна пределу ..Такие пределы встреч.при решении многих задач из разных областей науки,поэтому они получили спец.название «интеграл ф-ции от a до b» и обознач.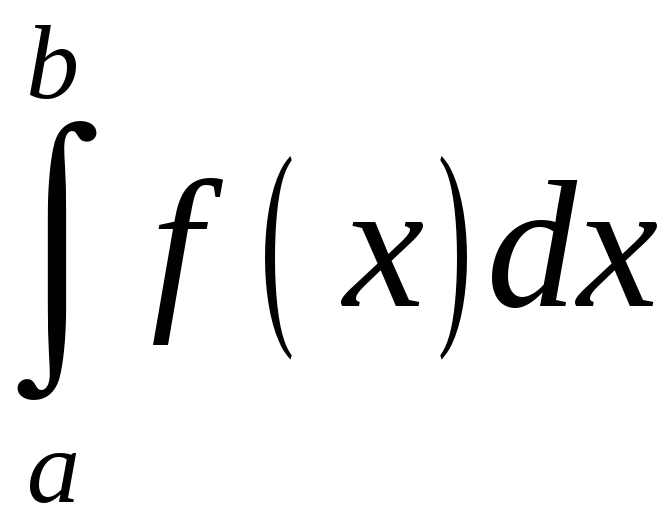.Сравнивая формулы площади кривол.трапеции и приходим к выводу -формула Н-Л.-эффектив.способ вычисления интегралов.

20. Проблемы построения школьного курса геометрии.

Курс геом-и занимает большое место и играет важную роль в школьном матем-ом образ-и. На него приходится около 40% уч. времени, отводимого на мат-ку в 5-11 классах, причем геом-я изуч-ся на протяжении всего времени обуч-я в школе. Осн. сод-е курса геом-и идет от начал Евклида. Целью изуч-я геом-и явл. разв-е лог. мышления, пространст-го представления и воображения. В последние годы наряду с традиц-ми методами геом-и, исп-х рав-во и подобие треуг-ков, тригонометрию и алгебру (ур-ния), в школьном курсе применяется аксиомат-й метод, метод геом. постр-й, корд-й и вект-й метод. Предпочтение отдаваемое тем или иным методам, в основном и отличает разные подходы к постр-ю курса геом-и сейчас.

Схема постр-я: 1)выбор неопред-х понятий (у Погорелова: точка, прямая, пл-ть; у Александрова: точка, отрезок, пл-ть) 2) постр-е сист. аксиом (св-ва: непротивореч-ть и незав-ть) 3) постр-е самой теории.