8.3. Метод объединения равнопотенциальных узлов.

Этот метод позволяет упрощать схемы электрических цепей путём объединения узлов, имеющих равные потенциалы в один узел.

Задача № 41. Найти сопротивление цепи АВ, изображённой на рис. 42,а.

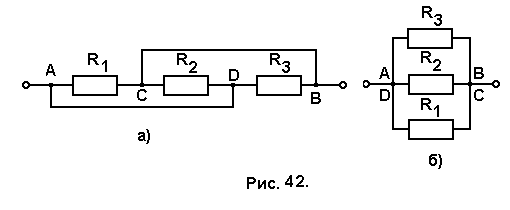
Так как сопротивление подводящих проводов считается равным нулю, то точки А и D, соединённые проводником имеют одинаковый потенциал, то же можно сказать и о потенциалах точек В и С. Объединив точки А и D в один узел и, сделав то же самое с точками В и С, получим простую схему из трёх параллельно соединённых резисторов (рис. 42,б). общее сопротивление цепи определим по формуле:

1/R_общ = 1/R₁ + 1/R₂ + 1/R₃, (8.11)

откуда

R_общ = R₁ R₂ R₃/( R₁R₂ + R₂R₃ + R₁R₃). (8.12)

Задача № 42. Найти сопротивление цепи, изображённой на рис.43,а, если сопротивления всех резисторов одинаковы и равны R.

Потенциалы точек 1 и 3 одинаковы, поэтому их можно объединить в одну, то же самое можно сделать с точками 2 и 5, 4 и 6. В результате получится видоизменённая упрощённая схема (рис. 43,б).

Резисторы R₁₂ и R₂₃ соединены параллельно, следовательно, их общее сопротивление равно R/2. Точно также общее сопротивление резисторов R₄₅ и R₅₆ равно R/2. Общее сопротивление части цепи параллельной R₃₄ равно R/2 + R/2 = R, поэтому сопротивление всей цепи будет равно R/2.

8.4. Метод разделения узлов.

Метод разделения узлов схемы основан на том, что, если возможно объединение двух узлов, имеющих равные потенциалы, то возможен и обратный переход: узел схемы можно разделить на две или несколько точек, если получившиеся при этом точки имеют прежние одинаковые потенциалы.

Задача № 43. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис.44) сопротивлением R каждый.

Разделим узел О на две точки, получив два варианта электрической цепи (рис. 45, а) и (рис. 45, б). В первом случае потенциалы точек О^’ и О^’’ не равны. , Если потенциал точки А больше потенциала точки В, то потенциал точки О^’ больше потенциала точки О^’’ и наоборот. Потенциалы же точек О₁ и О₂ равны, так как находятся в одинаковых условиях (полностью симметричны). Отсюда следует, что верным является разделение узла О, показанное на рис. 45, б. Эквивалентная схема цепи, полученная после разделения узла О, изображена на рис. 45, в. Отсюда общее сопротивление цепи между точками А и В равно 3R/2.

Задача № 44. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 46,а) сопротивлением R каждый.

Единственно верным способом разделения узла О на отдельные точки О₁, О₂ и О₃ является способ, изображённый на рис. 46,б. Эквивалентное сопротивление участков (cd) и (ef) будет равно

R_cd = R_ef = 2R R/ (2R + R) =2R/3. (8.13)

Эквивалентное сопротивление участка АО₁В равно 2R. Эквивалентная схема цепи, полученная после разделения узла О, изображена на рис. 46,в. Общее сопротивление цепи определим по формуле

1/ R_общ = 3/8R + 3/8R + 1/2R = 5/4R, (8.14)

откуда R_общ = 4R/5.