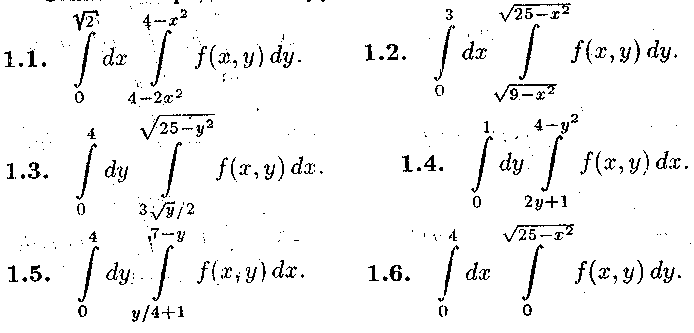3. Завдання теми 4

Задача № 1.

Розв'язати диференціальні рівняння. В пункті б) знай­ти частинний розв'язок, що задовольняє початковій умові

92 4. ТЕМА №4

3. ЗАВДАННЯ ТЕМИ 4 93

94 4. ТЕМА №4

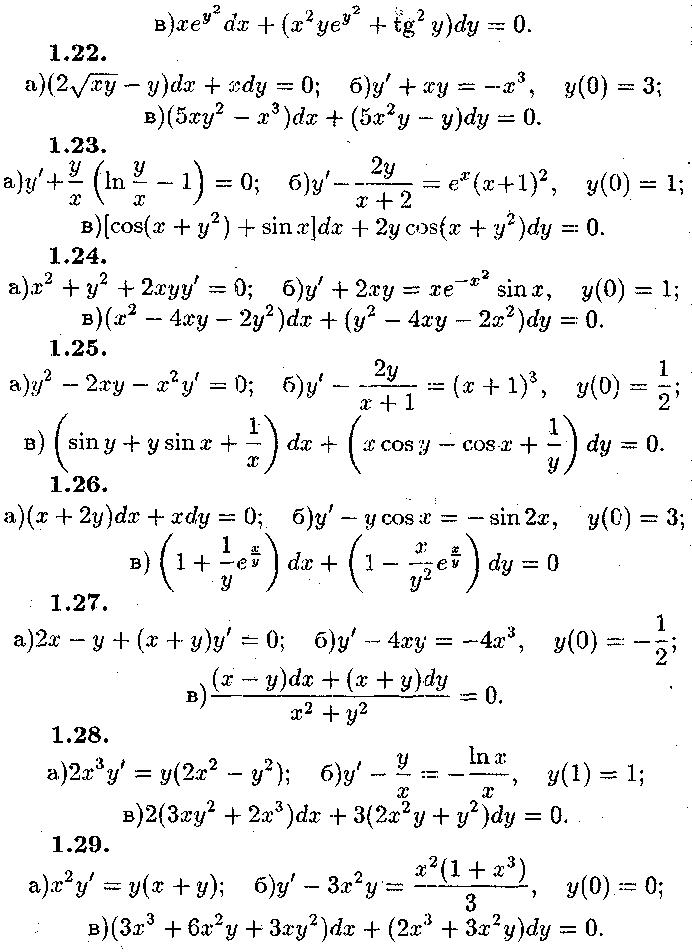
3. ЗАВДАННЯ ТЕМИ 4 95

Задача № 2.

Розв'язати диференціальні рівняння. В пункті в) знай­ди частинний розв'язок, що задовольняє початковим умо­вам

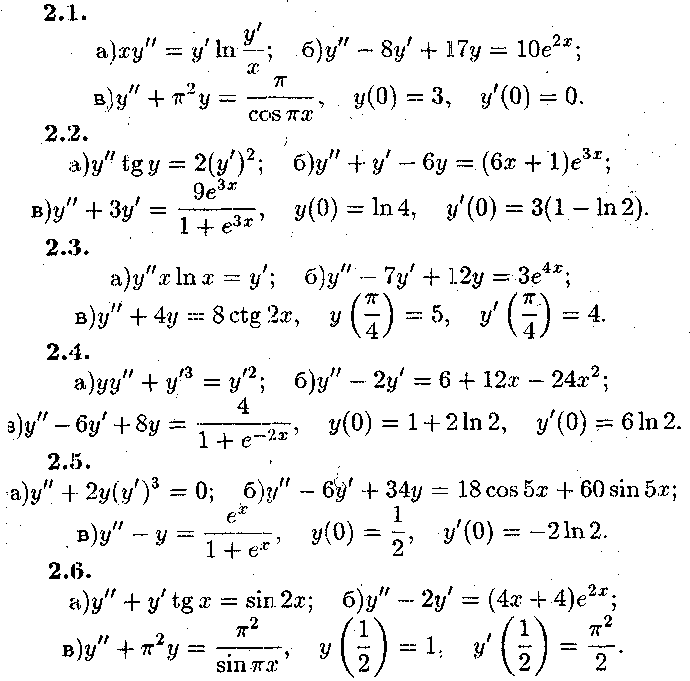
96 4. ТЕМА №4

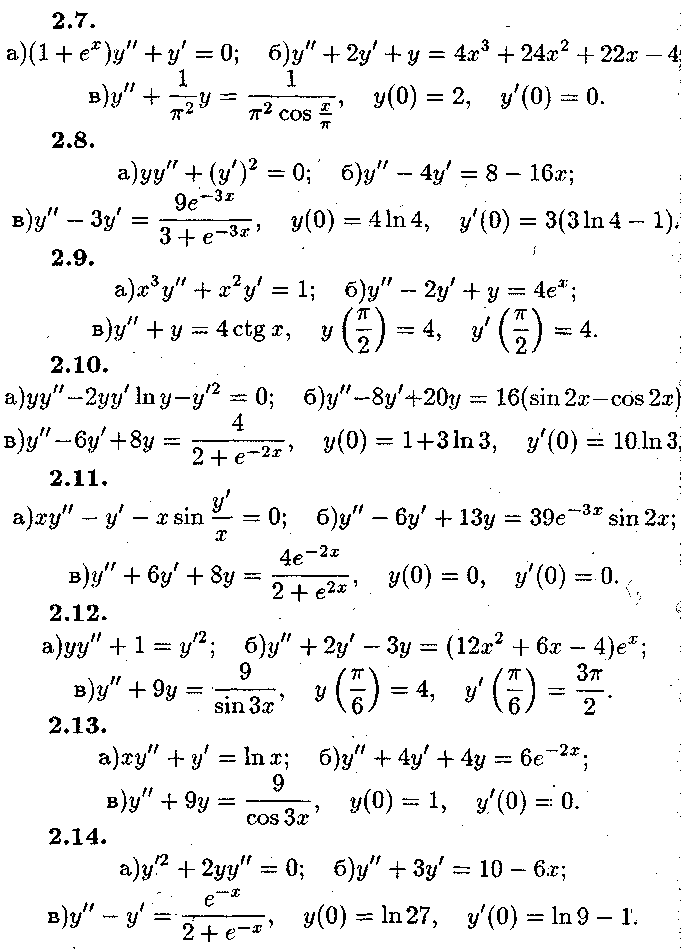
3. ЗАВДАННЯ ТЕМИ 4 95

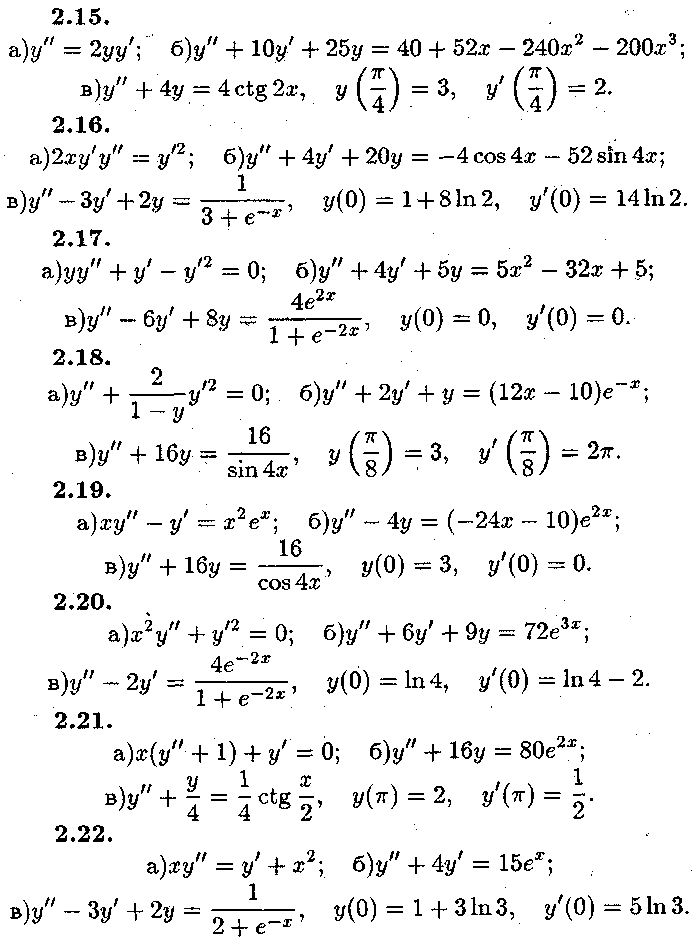
98 4. ТЕМА №4

3. ЗАВДАННЯ ТЕМИ 4 99

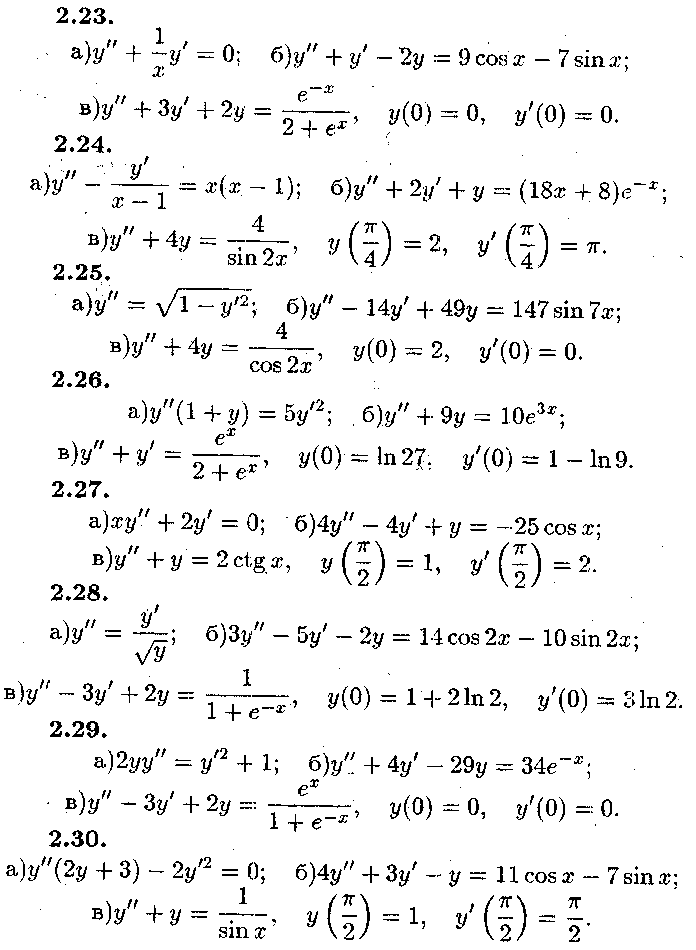
Задача № 3.

Розв'язати системи диференціальних рівнянь. Систему пункту а) розв'язати методом виключення. Систему пун­кту б) розв'язати за допомогою характеристичного рівня­ння, а також знайти частинний розв'язок, що задовольняє початковим умовам

S

100 4. ТЕМА №4

3. ЗАВДАННЯ ТЕМИ 4 101

'

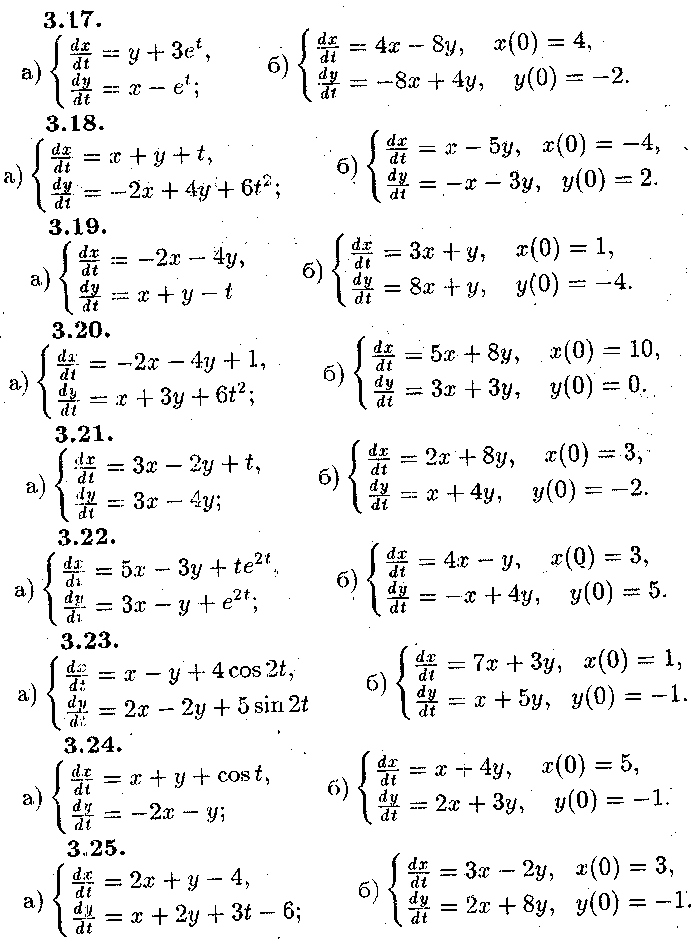
102 4. ТЕМА №4

ТЕМА№ 5

Кратні інтеграли та елементи векторного аналізу

Література: [1]Кн.2; [2]Ч.2; [3]Ч.1; [4]; [5]Кн.З.

1. Теоретичні питання

Подвійні та потрійні інтеграли, їх основні властивості. Поняття про n-вимірні інтеграли. Обчислення подівійних і потрійних інтегралів в декартових координатах. Заміна змінних в кратних інтегралах. Перехід від декартових до полярних, циліндричних та сферичних координат. Засто­сування кратних інтегралів до задач геометрії, механіки і фізики.

Задачі, що приводять до криволійних інтегралів. Озна­чення криволінійних інтегралів першого і другого роду, їх основні властивості та обчислення. Застосування криволі­нійних інтегралів до задач геометрії та механіки. Зв'язок між криволінійними інтегралами першого та другого роду. Формула Гріна.

Площа поверхні. Означення поверхневих інтегралів, їх властивості та обчислення.

103

104 5. ТЕМА №5

Скалярне поле. Поверхні та лінії рівня скалярного по­ля. Похідна за напрямом. Градієнт скалярного поля, йо­го координатне та інваріантне означення. Векторне поле. Векторні лінії та їх диференціальні рівняння.

Односторонні та двосторонні поверхні. Потік вектор­ного поля через поверхню. Фізичний зміст потоку в полі швидкостей рідини. Обчислення потоку. Теорема Остро-градського. Дивергенція векторного поля, її інваріантне означення і фізичний зміст. Обчислення дивергенції. Соле-ноїдальні (трубчасті) поля.

Лінійний інтеграл у векторному полі. Робота силового поля. Циркуляція веторного поля. Теорема Стокса. Ротор (вихор) поля, його координатне та інваріантне означення. Фізичний зміст ротора в полі швидкостей. Незалежність лінійного інтеграла від форми шляху інтегрування. Потен­ціальне поле, умова потенціальності поля. Обчислення лі­нійного інтеграла в потенціальному полі.

Оператор Гамільтона. Операції другого порядку у век­торному аналізі. Оператор Лапласа, його вираз у циліндри­чних і сферичних координатах.

2. Приклади

Приклад 1.: Змінити порядок інтегрування в повторному інтегралі

Розв'язок. Будуємо область інтегрування G за межами інтегрування'

(рис. 5.1)

2. приклади 105

Рисунок 5.1

Зверху область G обмежена кривою

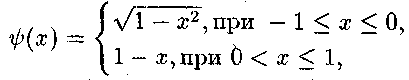
а знизу — прямою у — 0. Тому маємо

ПРИКЛАД 2. За допомогою подвійних інтегралів обчислити в полярних координатах площу плоскої фігури, яка обмеже­на лінією

Розв'язок.

Перейдемо до полярної системи координат,.

, в якій рівняннязаданої лінії матиме вигляд

.

Побудуємо криву (рис. 5.2)

106 5. ТЕМА №5

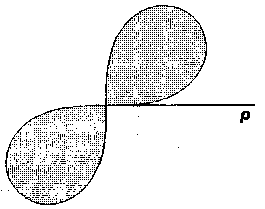
Рисунок 5.2

Рисунок 5.3

Вона симетрична відносно полюса і при зміні від 0 до поточна точка опише половину кривої. Тоді

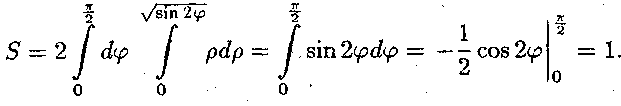
ПРИКЛАД 3.

Знайти об'єм тіла, обмеженого поверхнями

Розв'язок. Задане тіло є циліндроїдом, обмеженим звер­ху площиною х + z = 4, знизу площиною z = Q і боків пря­мими циліндрами(рис. 5.3а). Область інтегрування показана на рис. 5.36.

2. ПРИКЛАДИ 107

Маємо z = 4 — х

ПРИКЛАД 4. Обчислити криволінійні інтеграли

де L - відрізок прямої у = 2х — 2, який роз­ташованийміж точками А(0; —2), В(l;0).

якщо Lab- дуга параболи у = х²,яка розташована між, точками А(0,0) і В(2,4).

Розв'язок. а) ЗнайдемоОтже

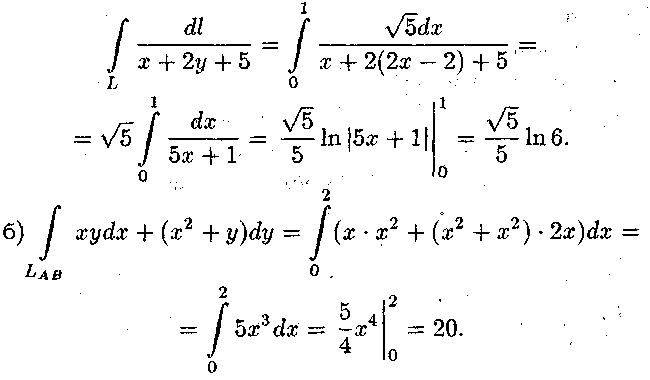
ПРИКЛАД 5. В пункті а) обчислити поверхневий інтеграл першого родупо поверхні S, де S - частина

108 5. ТЕМА №5

Рисунок 5.4

площини (р) : х + z — Чу = 2, яка відтинається координатни­ми площинами;'в пункті б) обчислити поверхневий інтеграл другого роду, де S - верхня сторона повер-

хніяка, відтинається площинами у = 0, у = 1

(рис. 5.4) . .

Розв'язок.

а) 3 рівняння площини знайдемо:

Зведемо обчислення поверхневого інтеграла до обчисле­ння подвійного інтеграла по області G, де G - трикутник АОВ₇ який є проекцією поверхні S на площину Оху (рис.

5.5) ..

Тоді

2. приклади 109

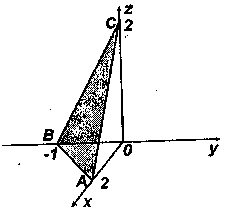
Рисунок 5.5

б) Проекцією G заданої поверхні на площину Оху є пря-

мокутник, який визначається нерівностями,

Тоді

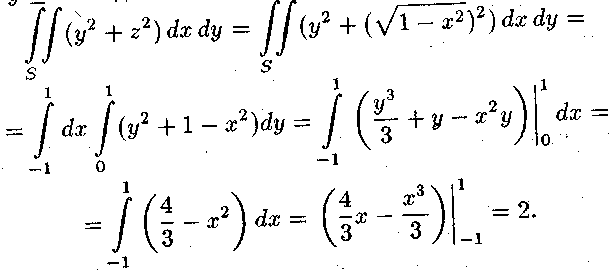
Приклад 6. Задано векторне поле

і площину x + y + z — 1 (р), яка разом зкоординатними площинами утворює піраміду V. Нехай S — основа піраміди, яка належить площині (р); L — контур, який обмежує S;— зовнішня нормаль до S. Обчисли­ти: а) циркуляцію векторного полявздовж замкненого

110 5. ТЕМА №5

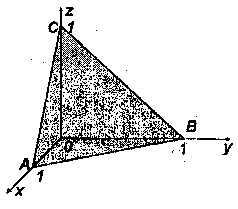
Рисунок 5.6

контура L, застосувавши формулу Стокса до контура L і обмеженої ним поверхні S з нормаллю; б) потік вектор­ного поля через повну поверхню піраміди V в напрямі зовнішньої нормалі до її поверхні, застосувавши формулу Остроградського.

Розв'язок.

а) Обчислимо циркуляцію векторного поля викори­стовуючи формулу Стокса

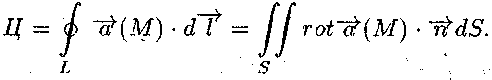
Для цього визначимо

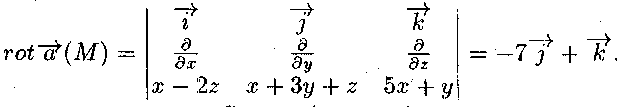
Застосуємо формулу Стокса (рис. 5.6)

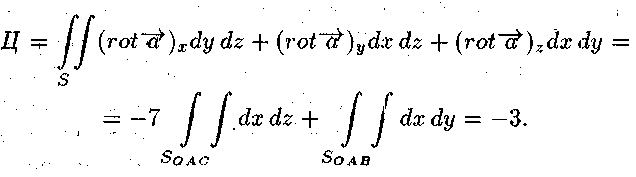
3. ЗАВДАННЯ ТЕМИ 5 111

б) Обчислимо потік векторного полячерез повну

поверхню піраміди, використовуючи формулу Остроград­ського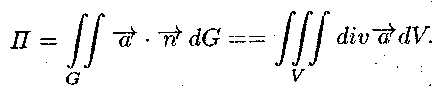

Знайдемо

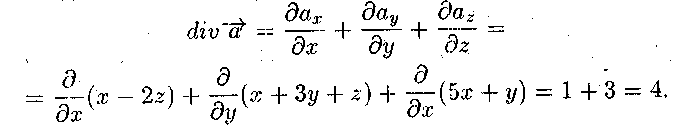
Тоді

3. Завдання теми 5

Задача № 1.

Змінити порядок інтегрування.