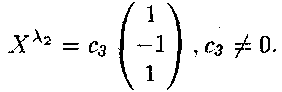2. Приклади

ПРИКЛАД 1. Скласти рівняння перпендикулярів, опущених з фокусів еліпса на асимптоту гіперболи

з додатнім кутовим коефіцієнтом. Зробити рисунок.

Розв'язок.

Запишемо рівняння еліпса і гіперболи (рис. 1.1) у ви­гляді

12 1.ТЕМА №і

Рисунок і.і

Фокуси еліпса розташовані на осі Оу і, оскільки с² = ЗО— 14 = 16, мають координати F₁ (0; —4), F₂(0;4)

Для заданої гіперболи рівняння асимптот мають вигляд Асимптотою з додатнім кутовим: коефіцієнтом є пряма Кутовий коефіцієнт прямих, перепендику-

лярних до асимптоти, дорівнює —2.

Рівняння перпендикуляра, опущеного з фокуса F₁ (0; —4) на асимптотумає вигляд

у + 4=-2х або 2х+у + 4 = 0.

Для перпендикуляра, опущеного з фокуса F₂ (0;4) на асимптотуматимемо

у - 4 = -2х або 2х + у-4 = 0.

ПРИКЛАД 2. Задані координати вершин піраміди ABCD : А(-2; 0;

-1); В(0; 0; 4); С(1; 3; 2); І>(3; 2; 7). Знайти: 1) дов­жину ребра АВ; 2) кут між ребрами АВ і AD; 3) рівняння площини ABC та кут між нею і ребром AD; 4) площу гра­ні ABC; 5) об'єм піраміди; 6) рівняння і довжину висоти, опущеної з вершини D на грань ABC; 7) рівняння площини, яка проходить через висоту піраміди, опущеної з вершини D на грань ABC і вершину А піраміди.

2. ПРИКЛАДИ 26

Розв'язок. Знайдемо коодинати векторів .= (2; 0; 5); ={3;3;3);= (5; 2; 8). Тоді

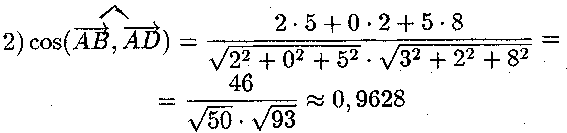
і кут між ребрами АВ і AD приблизно дорівнює 15°41';

3) Рівняння площини ABC запишемо у вигляді

або, розкривши визначник 5х — Зу — 2z + 8 = 0.

Звідси знаходимо координати вектора нормалі площини = (5; —3; —2) та синус кута φ між ребром AD і гранню АВС

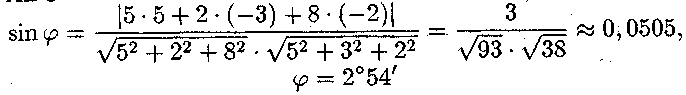
4) Площа грані дорівнює половині модуля векторного до-

бутку

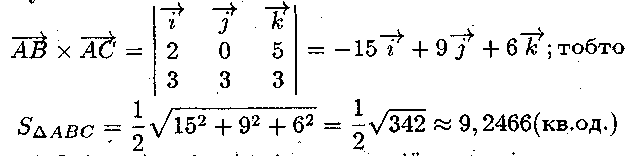
5) Об'єм піраміди дорівнює шостій частині модуля змі­шаного добутку трьох векторів, тобто

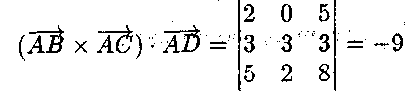
\14 1: ТЕМА №1

6) Рівняння висоти, опущеної з вершини D

Довжина цієї висоти дорівнює відстані від точки D до пло­щини ABC

4. Знайдемо вектор нормалі шуканої площини

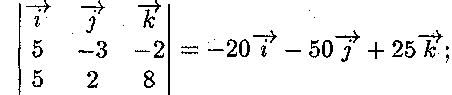
Тоді -4(х + 2) - 10у + 5(z + 1) = 0 або -4х - 10у + 5z - 3 = 0 — рівняння шуканої площині.

ПРИКЛАД 3. Довести сумісність системи рівнянь і знайти розв'язок в пункті а) методом матричного числення, в пун­кті б) методом Жордана-Гаусса.

Розв',язок..

а) Запишемо матриці,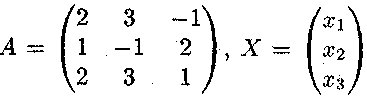

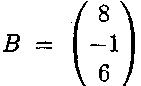. В матричній формі задана система рівнянь

2. Приклади 15

запишеться АХ = В. Матриця А невироджена, оскільки і, отже існує обернена. Система рівнянь має єдиний розв'зок

Знайдемо алгебраїчні доповнення елементів матриці А

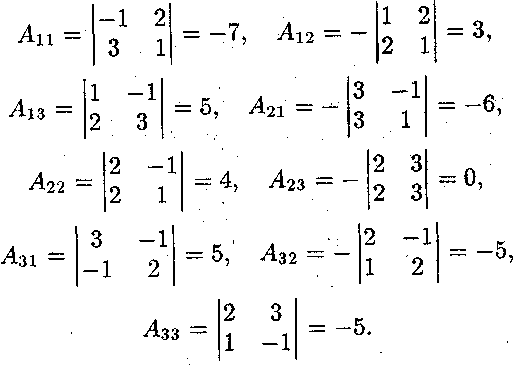
Тоді обернена матриця має вигляд

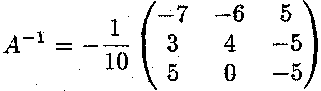
і розв'язоксистеми рівнянь

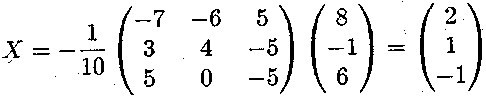
б) Проведемо елементарні перетворення над рядками розширеної матриці, одержимо

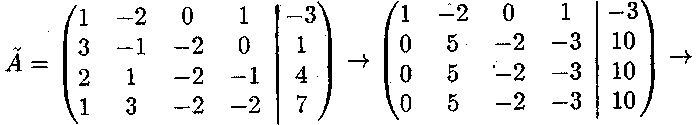
16 1. ТЕМА №1

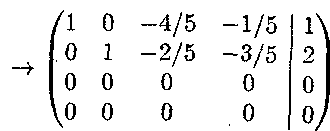
Перші два рядки останньої матриці є розширеною матри­цею системи

що еквівалентна заданій системі. Вважаючи xj,x₂ базис­ними невідомими, вільними, одержимо загальний розв'язок у вигляді

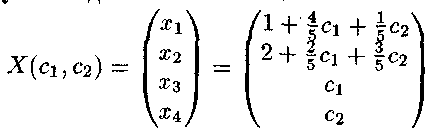
ПРИКЛАД 4. Лінійний оператор в деякому базисі заданий

матрицею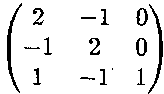. Знайти власні числа і власні век-

тори цього лінійного оператора.

Розвиток. Характеристичне рівняння

і

звідки— власні числа оператора. Знайдемо

власні вектори, що відповідають власному числу= 1. При= 1 системаприймає вигляд

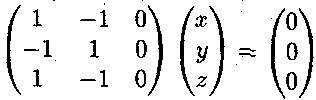
3. ЗАВДАННЯ ТЕМИ 1 17

Фундаментальна система розв'язків

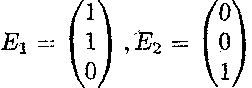
а загальний розв'язок

,

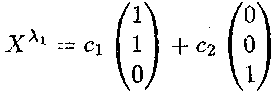де c₁ і с₂ не дорівнюють нулю одночасно.

Аналогічно розглядається випадок=-3. При цьому одержимо