3. Завдання теми 3 79

Задача № 4.

Обчислити невласний інтеграл або встановити його ро-

84 3. ТЕМА №3.

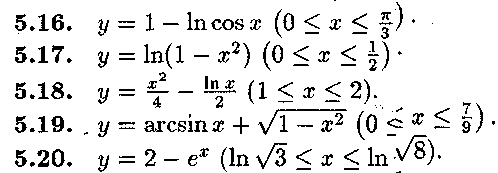
Знайти об'єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої лініями

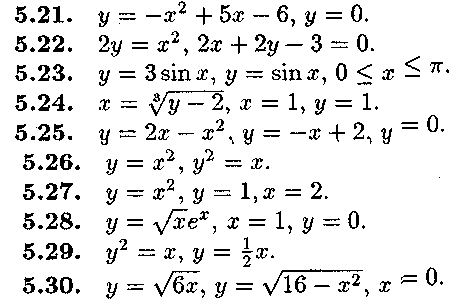
ТЕМА № 4

Диференціальні рівняння

Література: [1]Кн.2; [2]Ч.2; [3]Ч.2; [4]; [5]Кн.З; [9].

1. Теоретичні питання

Диференціальні рівняння першого порядку. Задача Ко­ші. Теорема існування і єдиності розв'язку задачі Коші. Ос­новні типи диференціальних рівнянь, що інтегруються в квадратурах: рівняння з відокремлюваними змінними, од­норідні рівняння та звідні до них, лінійні рівняння, рівняння .Бернуллі, рівняння в повних диференціалах.

Диференціальні рівняння вищих порядків. Задача Ко­ші. Теорема існування і єдиності розв'язку задачі Коші. Рі­вняння, які дозволяють знизити їх порядок.

Лінійні диференціальні рівняння: однорідні і неоднорі­дні. Структура загального розв'язку. Метод Лагранжа ва­ріації довільних сталих. Лінійні диференціальні рівняння із сталими коефіцієнтами. Рівняння з правою частиною спе­ціального виду.

Нормальні системи диференціальних рівнянь. Задача Коші. Теорема існування і єдиності розв'язку задачі Коші. Метод виключення. Нормальні системи лінійних однорі­дних диференціальних рівнянь зі сталими коефіцієнтами. Розв'язування з допомогою характеристичного рівняння.

85

86 4. ТЕМА №4

2. Приклади

ПРИКЛАД і. Розв'язати диференціальні рівняння. В пункті б) знайти частинний розв'язок, що задовольняє початковій умові у(х₀) = у₀.

Розв',язок.

а) Це рівняння — однорідне. Застосовуючи підстановку

у= их, матимемо + и = и + 1, або

Звідси або остаточно

б) Задане рівняння— лінійне. Шукаємо розв'язок цього

РІВНЯННЯ у ВИГЛЯДІ у= и (х) υ( х) Маємо

Виберемо функцію v так, щоб

Для знаходження v маємо рівняння з відокремлюваними змінними, розв'язавши яке, знаходимо одну з таких функцій

Тоді функцію и знаходимо із рівняння

або

Таким чином

-загальний розв'язок рівняння. Виходячи з початкової умо­ви, одержуємозвідки С = — 1. Шуканий частин­ний розв'язок

2. ПРИКЛАДИ 87

в) Оскільки то задане рівняння є рівнянням в повних диференціалах. Знайдемо функцію U(x,y), повний диференціал якої dU = дорівнює лівій частині заданого рівняння, тобто таку, шо

Інтегруємо по х перше з двох останніх рівнянь, вважаючи

у сталим

тоді

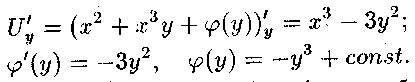
Отже, загальний розв'язок заданого рівняння буде мати ви­гляд

ПРИКЛАД 2. Розв'язати диференціальні рівняння. В пункті в) знайти частинний розв'язок, що задовольняє початковим

умовам

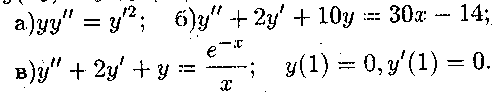
Розв',язок.

а) В рівняння не входить х. Нехай ; Тоді

Одержане рівняння має розв'язок р = 0 і, отже, у = С є розв'язком даного рівняння. Вважаючи тепер, ско-

рочуючи на р і відокремлюючи змінні, маємоІнте-

груючи, одержуємо р = С₁у; звідси у' = С₁у: 3 останнього

88 4. ТЕМА №4

рівняння одержимо

Розв'язок у = С також задається цим виразом при С₁ = 0.

б) Характеристичне рівняннямає корені к1 = — 1 + Зі; к2 = —1 — Зі. Загальний розв'язок відповід­- ного однорідного рівняння Частинний розв'язок у₁ шукаємо у вигляді у₁ = Ах + В., Продиференціюємо у₁два рази і підставимо в задане рів-, няння

Звідси А = З, В = —2 і у₁ (х) = Зх — 2.

Загальнийрозв'язок заданого рівняння

в) Характеристичне рівняння відповідного однорідного рівняннямає корені к₁= к₂ = — 1. Тому два лінійно незалежні розв'язки однорідного рівняння є у₁ =

а його загальний розв'язок

Розв'язок неоднорідного рівняння шукаємо у вигляді

Для знаходження С₁(х) і С₂(х) одержуємо систему

Звідси Тоді

де Сі і Сі - довільні сталі і, отже, за­гальний розв'язок

2. ПРИКЛАДИ 89

Виходячи з початкових умов, одержуємо

тобто С₁ = 1, С₂ = 0.

Шуканий частинний розв'язок

ПРИКЛАД 3. Розв'язати системи диференціальних рівнянь. Систему пункту а) розв'язати методом виключення. Систе­му пункту б) розв'язати за допомогою характеристичного рівняння, а також знайти частинний розв'язок, що задо­вольняє початковим умовам х(0) = х_о,у(0) = уо

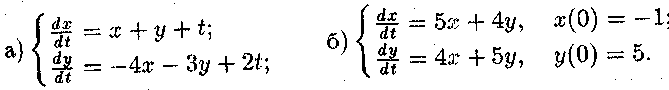
Розв'язок.

а) Продиференціюємоперше рівняння по t:

Із системи одержуємо' х" = х + у + t — 4х — Зу + 2 t + 1 або= — Зх — 2у + З t + 1. З першого рівняння системи

у =— х — t. Підставивши в одержане рівняння, маємо = -Зх - 2(х' - х -t) +3 t +1 або х" + 2х' + х = 5 t + 1,

Загальним розв'язком останнього рівняння є функція

Тоді

Отже загальний розв'язок

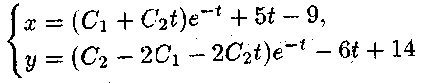
90 4. ТЕМА №4

б) Складаємо і розв'язуємо характеристичне рівняння

Для кореня к1 = 1 знаходимо власний вектор (a_{1 ,} β₁), роз­в'язуючи систему

, знаходимо а₁ = — β₁ і, отже, вектор (1; — 1) — власний, а - частинний розв'язок системи.

Для кореня к ₂ = 9 знаходимо власний вектор (a_{2 ,} β₂), розв'язуючи систему

■>

Знаходимо a₂₌ β₂ і, отже, вектор (1;1) — власний, а х₂ — — частинний розв'язок системи.

Загальний розв'язок записується через два знайдених лінійно незалежних розв'язки.

Використавши початкові умови, одержимо:

Звідси маємо С₁= —3; С₂ = 2. Частинний розв'язок систе­ми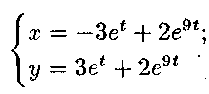

3. ЗАВДАННЯ ТЕМИ 4 91