Системы обработки сигналов

Физические системы. Радиотехническое устройство независимо от своего назначения и уровня сложности представляет собой систему, т.е. совокупность физических объектов, между которыми существуют определенные взаимодействия.

Системы, применяемые для обработки, преобразования и передачи сигналов, весьма разнообразны по принципам внутреннего устройства и внешним характеристикам. Основными современными средствами обработки сигналов являются, как аналоговые, так и цифровые радиоэлектронные устройства с фиксированной и программируемой логикой работы (могут быть и гидравлические, и оптические, и др.). Вне зависти от физического принципа работы системы используются универсальные принципы описания параметров систем.

Системы(вставить далее по тексту?)

Теорию систем принято делить на два раздела – анализ и синтез.

1) Анализ существующих систем. Задачей анализа является нахождение внешних характеристик системы (системной функции Т), например, заданной в виде электрической принципиальной схемы.

Также в этом разделе изучается:

а) Прохождение сигналов через системы обработки (y по x и Т)- прямая задача,

б) Восстановление сигнала на входе системы x по известному выходному сигналу y и системной функции Т – обратная задача.

в) Определение системной функции Т по известным входному x и выходному сигналу y системы.

2) Синтез систем обработки сигналов. Задача синтеза – нахождение структуры системы реализующей заданную внешнюю характеристику. Синтез, как правило, является неоднозначной процедурой, т.е. одинаковыми свойствами могут обладать множество структур. Метод синтеза должен быть в определенном смысле оптимальным, т.е. цепь должна содержать минимальное количество элементов и пр.

- прямая задача, т.е. конструирование такой системы, которая из исходного сигнала получает измененный сигнал с заданными свойствами: фильтрация (эквалайзеры),

-обратная задача, т.е. конструирование такой системы, которая из искаженного сигнала позволяет восстановить исходный сигнал, возможно с некоторой ошибкой: восстановление сигналов (очистка звука и изображения от помех и шумов, компенсация искажений).

Системные операторы. В структуре системы можно выделить вход, на который подается исходный сигнал, и выход, откуда снимается преобразованный сигнал. Если интересуются лишь связью между сигналами на входе и выходе и не описывают внутренние процессы в системе, то говорят, что система представляет собой «черный ящик».

В наиболее простом случае как входной сигнал , так и выходной сигнал , называемый также откликом или выходной реакцией системы, описываются одиночными функциями времени. В более общем случае входной сигнал представляется в виде т-мерного вектора

а выходной сигнал — в виде n-мерного вектора

Закон связи между сигналами и задают системным оператором Т, результатом воздействия которого на сигнал служит сигнал

.

Оператор Т[·] может представлять собой правило или набор правил, по которым происходит отображение входного сигнала на выходной, или даже таблицу соответствия выходных сигналов различным входным сигналам. Широкое применение получил метод описания физических систем в виде дифференциальных уравнений.

Чтобы полностью определить задачу, следует указать также область D_in некоторого функционального пространства, которая называется областью допустимых входных воздействий. Задание этой области описывает характер входных сигналов, которые могут быть непрерывными или дискретными, детерминированными или случайными. Подобным же образом должна быть указана область D_out допустимых выходных сигналов.

Математической моделью системы называют совокупность системного оператора Т и двух областей допустимых сигналов D_in, D_out.

Классификацию систем проводят на основании существенных свойств их математических моделей.

Линейные динамические системы

Линейными динамическими системами принято называть устройства, характеризуемые следующим свойством: их выходной сигнал определяется не только величиной входного сигнала в рассматриваемый момент времени, но и «предысторией» этого сигнала. Иначе говоря, динамическая система обладает некоторой конечной или бесконечной «памятью», от характера которой зависят особенности преобразования входного сигнала.

Системы, описываемые дифференциальными уравнениями. Среди всевозможных динамических систем большое значение для теоретической радиотехники имеют те, которые описываются дифференциальными операторами. В общем случае речь идет о системах, для которых связь между одномерными входным и выходным сигналами устанавливается с помощью следующего дифференциального уравнения:

. (*)

Именно такой оказывается динамическая связь между мгновенными значениями входного и выходного сигналов в электрической цепи с сосредоточенными параметрами. Если цепь линейна и стационарна, то все коэффициенты a и b – постоянные вещественные числа.

Сосредоточенные и распределенные физические системы.

Одним из критериев классификации физических радиотехнических систем является сопоставление физических размеров системы и рабочей длины волны.

Если характерный размер системы (например, наибольшая длина соединительных проводников цепи) оказывается гораздо меньше длины волны, то получается сосредоточенная система. Такая система может быть описана обычным дифференциальным уравнением. Анализ и расчет сосредоточенных радиотехнических систем проводят с помощью известных законов Кирхгофа.

В сосредоточенной электрической цепи всегда можно выделить физические области с преимущественной локализацией энергии электрического поля (конденсаторы) и магнитного поля (индуктивные элементы). Свойства сосредоточенных цепей слабо зависят от конфигурации соединительных проводников, поэтому для описания таких цепей принято использовать их абстрактные модели, называемые принципиальными схемами.

Например: RC- интегратор или LC колебательный контур.

На частотах в несколько Гигагерц (длина волны порядка 10 см), в так называемом сверхвысокочастотном (СВЧ) диапазоне, физические размеры большинства устройств оказываются сравнимыми с длиной волны передаваемых колебаний, так что становится необходимым учет конечного времени распространения сигнала. Обычные электрические цепи в столь высокочастотном диапазоне уже не могут использоваться и на смену им приходят системы с распределенными параметрами (распределенные или волновые системы). Такие системы могут быть описаны дифференциальным уравнением в частных производных.

Так, вместо соединительных проводников применяются отрезки металлических труб — волноводы, вместо колебательных LC-контуров — их распределенные аналоги, называемые объемными резонаторами. Теория, методы анализа и проектирования распределенных систем достаточно сложны и составляют содержание отдельных радиотехнических дисциплин.

Например: RC- интегратор или LC колебательный контур.

Линейные и нелинейные системы. Важнейший принцип классификации систем основан на том, что различные системы по-разному ведут себя при подаче на вход суммы нескольких сигналов. Если оператор системы таков, что справедливы равенства

, - свойство аддитивности

, - свойство однородности

где α — произвольное число, то данная система называется линейной. Условия выражают фундаментальный принцип суперпозиции.

Суперпозиция (принцип наложения или принцип независимости действия) – отклик линейной системы на взвешенную сумму входных сигналов равен взвешенной сумме откликов на отдельные входные сигналы, т.е. входной сложный сигнал раскладывается на составляющие и отдельно определяется выходной сигнал для каждой составляющей и суммируются. (В линейной системе действие суммы причин равно сумме действий, вызываемых каждой отдельно взятой причиной).

Систему называют линейной в том и только том случае, когда она удовлетворяет двум условиям: 1) если ее входной сигнал является суммой двух последовательностей, то выходной сигнал является суммой двух соответствующих выходных последовательностей; 2) пропорциональное изменение входного сигнала приводит к пропорциональному изменению выходного сигнала. Таким образом, если преобразование L[•] описывает действие линейной системы и;, то для всех входных сигналов х₁ и х₂ и любых комплексных констант а и b.

- линейная система, -нелинейная система.

Линейная система (инерциальная и неинерциальная) описывается линейным дифференциальным уравнением, т.е. коэффициенты которого не зависят от сигнала.

Например, рассмотрим одиночный колебательный контур, находящийся в свободном режиме. Такой цепи соответствует однородное дифференциальное уравнение второго порядка.

Нелинейная система описывается дифференциальным уравнением, хотя бы один коэффициент которого зависит от сигнала, условия (4) не выполняются.

Например: .

Стационарные и нестационарные системы. Принято говорить, что система стационарна (инвариантна к сдвигу), если ее выходная реакция не зависит от того, в какой момент времени поступает входной сигнал или точнее сдвиг входной последовательности приводит к соответствующему сдвигу выходной последовательности.

Если Т — оператор стационарной системы, то из равенства

(2)

следует, что

(3)

при любом значении t₀.

Например, для двумерной стационарной системы выполняются следующие выражения

для всех последовательностей х и для всех целочисленных сдвигов (m₁, m₂).

Стационарные системы называют также системами с постоянными во времени параметрами. Если же свойства системы не инвариантны относительно выбора начала отсчета времени, то такую систему называют нестационарной (системой с переменными во времени параметрами или параметрической системой).

Линейно-параметрическая система описывается линейным дифференциальным уравнением с переменными коэффициентами (параметрическим дифференциальным уравнением). Хотя бы один коэффициент, которого является функцией времени или координаты, но не входного сигнала. Выполняется принцип суперпозиции.

Например: .

В этом уравнении коэффициент является функцией времени (аргумента t).

Нелинейно-параметрическая система описывается дифференциальным уравнением, коэффициенты которого являются функцией входного сигнала и зависят от времени. Не выполняется принцип суперпозиции.

Например: .

Строго говоря, все физические системы, с которыми имеет дело радиотехника, в той или иной степени нелинейны и нестационарны. Однако существует много систем, которые весьма точно описываются линейными моделями. Так, практически всегда можно пренебречь нелинейностью обычных резисторов, конденсаторов и некоторых индуктивных элементов.

Нелинейные радиотехнические устройства содержат в себе обычно такие элементы, как полупроводниковые диоды и транзисторы, имеющие вольт-амперные характеристики сложного вида, а также квантователи в составе АЦП.

Теория нелинейных систем оказывается, как правило, довольно сложной. Далеко не все результаты могут быть получены здесь аналитическим путем. Однако именно с помощью нелинейных элементов осуществляются важнейшие преобразования радиотехнических сигналов.

Важным признаком классификации систем является возможность возникновения в результате преобразования сигнала колебаний новых частот, т.е. преобразование спектра сигнала. Т.к. гармонические функции являются собственными функциями операторов интегрирования и дифференцирования, то в линейных стационарных системах появления составляющих сигнала с новыми частотами не происходит. В нелинейных и параметрических системах происходит преобразование спектра с появлением новых частот.

Линейные стационарные системы (ЛС-системы) или линейные системы, инвариантные к сдвигу (ЛИС-системы).

Закончив краткий обзор принципов классификации систем, сконцентрируем внимание на простейшем их виде — линейных стационарных системах с сосредоточенными параметрами

Линейность и инвариантность к сдвигу являются независимыми свойствами системы; ни одно из этих свойств не подразумевает обязательного наличия другого. Например, пространственное маскирование

L [x (n₁, п₂)] = с(п₁, п₂) х(п₁, п₂)

приводящее к умножению входной последовательности на с(п₁, п₂), линейно, но не инвариантно к сдвигу.

С другой стороны, система

Т[х(n₁, n₂)] = [х(n₁, n₂)]²

инвариантна к сдвигу, но не линейна.

Эти системы отличаются простотой, как при разработке, так и при анализе, но в то же время они обладают достаточными возможностями для решения многих практических задач - это наиболее часто изучаемый класс систем для обработки дискретных сигналов любой размерности. Поведение этих систем во многих случаях можно изучать безотносительно к конкретным характеристикам входного сигнала. Разработана достаточно полная теория анализа на основе принципа суперпозиции( нахождение выходной реакции по входному воздействию и системному оператору или нахождение неизвестного входного воздействия по известной выходной реакции и системному оператору) и множество методик конструктивного синтеза систем (определить структуру и внутренние параметры системы по требуемому системному оператору).

Далее будут рассматриваться только линейные стационарные системы, если не оговорено иного.

Методы анализа прохождения сигналов через системы обработки

Замечательная особенность линейных систем — справедливость принципа суперпозиции — открывает прямой путь к систематическому решению задач о прохождении разнообразных сигналов через такие системы. Способ динамического представления позволяет представлять сигналы в виде сумм элементарных импульсов. Если удастся тем или иным способом найти реакцию на выходе, возникающую под воздействием элементарного импульса на входе, то окончательным этапом решения задачи явится суммирование таких реакций.

Намеченный путь анализа основан на временном представлении свойств сигналов и систем. В равной мере применим, а порой и гораздо более удобен анализ в частотной области, когда сигналы задаются рядами или интегралами Фурье. Свойства систем при этом описываются их частотными характеристиками, которые указывают закон преобразования элементарных гармонических сигналов.

Выбор наиболее удобного метода анализа зависит от структуры цепи, вида воздействующего сигнала, а также от того, в какой форме (частотной или временной) должен быть представлен выходной сигнал. Например, анализ прохождения относительно простых сигналов (импульсов включения, гармонических функций и т.п.) через цепи, которые описываются линейными дифференциальными уравнениями не выше второго порядка, достаточно просто выполняется классическим методом дифференциальных уравнений.

В тех случаях, когда решение дифференциальных уравнений затрудняется (воздействие сложных сигналов на цепи со сложной структурой), целесообразно использовать такие методы, как спектральный (операторный) или метод интеграла наложения (Дюамеля), основанные на принципе суперпозиции.

Прохождение сигналов через апериодические цепи и избирательные цепи

Точные методы анализа

-метод дифференциальных уравнений

- операторный

-спектральный (операторный)

-метод интеграла наложения (Дюамеля)

При анализе прохождения сигналов через узкополосные системы, помимо перечисленных методов анализа, дающих точное решение, применяются приближенные методы, позволяющие для ряда задач получить решения, достаточно близкие к точным.

Прохождение сигналов через избирательные цепи

Приближенные методы анализа

-метод огибающей(спектральный метод и метод интеграла Дюамеля для комплексной огибающей)

-метод «мгновенной» частоты

-приближенный спектральный метод

Классический метод анализа переходных процессов

Линейное однородное дифференциальное уравнение с постоянными коэффициентами.

Предположим, что входной сигнал u_BX(t) задан. Тогда правая часть уравнения, которую можно условно обозначить f(t), является известной функцией. Анализ поведения системы сводится при этом к хорошо изученной в математике проблеме решения линейного дифференциального уравнения n-го порядка с постоянными коэффициентами:

.

Порядок n этого уравнения принято называть порядком динамической системы.

Метод решения линейного однородного дифференциального уравнения с постоянными коэффициентами.

Примеры простейших схем, составления уравнений и решений.

Пример. Дана RC-цепъ вида Т-образного четырехполюсника, возбуждаемая со стороны входа источником ЭДС u_BX(t). Выходным сигналом служит напряжение на конденсаторе.

Поскольку ток в цепи , используя второй закон Кирхгофа, получаем дифференциальное уравнение

Итак, RС-цепь служит примером динамической системы 1-го порядка. Важнейший параметр этой цепи — постоянная времени τ = RС, определяющая характерный временной масштаб протекания процессов в системе.

Операционный метод. Преобразования Лапласа

Решение дифференциальных уравнений операторным методом. Преобразование Лапласа является исключительно гибким и мощным методом, позволяющим путем стандартных процедур находить решения линейных дифференциальных уравнений с постоянными коэффициентами. Именно это свойство обусловило его широкое использование в научных исследованиях и инженерных расчетах.

Пусть дифференциальное уравнение

(8-71)

устанавливает закон соответствия между сигналами на входе и выходе некоторой линейной стационарной системы.

Наложим некоторые ограничения. Сделаем допущение, что входной сигнал при t<0. Кроме того, исходя из специфики работы радиотехнических устройств, начальные условия выберем нулевыми: . Наконец, примем, что область допустимых входных сигналов не содержит в себе функций, столь быстро нарастающих во времени, что для них не существует преобразования Лапласа.

Метод операционного исчисления основан на том, что над оператором дифференцирования и некоторой функцией (изображением) X(s) от этого оператора, призводяться такие действия, что дифференцированию функции x(t) соответствует умножению оператора s на функцию X(s):

а интегрированию- деление функции X(s) на оператор s:

.

Обозначим закон соответствия между оригиналами и изображениями следующим образом:

,

Вычислив преобразования Лапласа от обеих частей дифференциального уравнения ( ) уравнения, получим

(8.72)

Важнейшей характеристикой, на которой основан операторный метод, является отношение изображений выходного и входного сигналов:

называемое передаточной функцией или операторным коэффициентом передачи рассматриваемой системы.

В соответствии с формулой (8.72)

(8.74)

Если эта функция известна, то поиск выходной реакции системы на заданное входное воздействие разбивается на три этапа:

l. ,

2. ,

|3. .

Термин «операторный метод» исторически восходит к известным работам Хевисайда, который еще в конце прошлого века предложил символический способ решения дифференциальных уравнений, описывающих переходные процессы в линейных электрических цепях. Метод Хевисайда основан на символической замене оператора дифференцирования d/dt комплексным числом s.

Свойства передаточной функции. Сравнивая формулы (8.74) и (8.41), можно убедиться, что функция К(s) есть результат аналитического продолжения частотного коэффициента передачи К(jω) с мнимой оси jω на всю плоскость комплексных частот .

Функция К(s) аналитична на всей плоскости s, за исключением конечного числа точек p₁, p₂…p_n, являющихся корнями знаменателя в формуле (8.74). Данные точки, т.е. корни уравнения

называют полюсами передаточной функции К(р).

Точки z₁, z₂,.. .,z_m, представляющие собой корни уравнения

,

называют нулями данной передаточной функции.

Вынося общий множитель К₀, возникающий при делении в (8.74) числителя на знаменатель, получаем так называемое нуль-полюсное представление передаточной функции:

(8.75)

Вещественность коэффициентов дифференциального уравнения (8.72) обусловливает следующее свойство нулей и полюсов: все эти числа либо вещественны, либо образуют комплексно-сопряженные пары.

Часто используют наглядный прием отображения передаточной функции с помощью карты нулей и полюсов, на которой некоторыми условными значками нанесены указанные точки. Саму функцию К(р), принимающую комплексные значения, нельзя непосредственно представить графически. Поэтому поступают так: над плоскостью с декартовой системой координат изображают трехмерную поверхность функции |К(s)| (рис. 8.4).

Поверхность имеет характерный вид «горного ландшафта»; бесконечно высокие вершины соответствуют полюсам, а впадины — нулям передаточной функции. Выполнив сечение этой поверхности с помощью плоскости, содержащей как вертикальную ось, так и ось jω, получим профиль АЧХ системы.

Рис. 8.4. Характер поверхности |К(s)| для передаточной функции, имеющей два комплексно-сопряженных полюса и один нуль z = 0

Полюсы передаточной функции линейной системы являются корнями характеристического уравнения (8.36). Поэтому для устойчивости системы необходимо и достаточно, чтобы эти полюсы располагались строго в левой полуплоскости комплексной переменной s. Нули передаточной функции в общем случае могут располагаться как в левой, так и в правой полуплоскостях.

Формула обращения. Заключительным этапом решения задачи о прохождении сигнала через линейную стационарную систему с помощью операторного метода является поиск оригинала, которому отвечает изображение ивъа(р) = = K(p)Um(p).

Рассмотрим частный случай, когда функция t/Bb[X(p) представляет собой отношение двух многочленов по степеням комплексной частоты:

Umui(p) = M(p)/N{p),

причем будем считать, что степень числителя m не пре­восходит степени знаменателя п и, кроме того, корни знаменателя ph i = 1, 2,..'. ,и — простые.

Способ нахождения оригинала, отвечающего такому изображению, основывается на представлении функции и*ы*(р) в виде суммы элементарных дробей:

Коэффициенты С,- являются вычетами функции 1/вых(р) в точках полюсов, поэтому [14]

Как известно, изображению 1/(р — pi) соответствует оригинал exp(p;t). Таким образом, приходим к известной Ф'нгл формуле обращения:

(8.76)

Примеры нахождения выходных сигналов операторным методом. При практическом использовании операторного метода большую часть формальных вычислений можно исключить, обращаясь к широко распространенным табли­цам преобразований Лапласа.

Пример . Найти переходную характеристику RC-цепи.

Здесь o(t)«->l/p, К(р) = 1Д1 +рт), поэтому 1/ВЬ1Х(р) = ]/[р(1+рт)]. Разлагая эту функцию на элементарные дроби, имеем

Оригиналы, соответствующие обоим слагаемым в правой части последней формулы, хорошо известны (см. [5, 6, 36]). Искомый

Передаточная функция равна отношению преобразования Лапласа реакции усилителя к изображению воздействия , вызвавшего эту реакцию, при нулевых начальных условиях. Пусть

;

- изображения Лапласа для входного и выходного сигнала при нулевых начальных условиях. Передаточная функция усилителя

является функцией комплексного аргумента . Вид многочленов и и коэффициенты их зависят только от схемы цепи (усилителя) и параметров ее элементов.

Формально передаточная функция может быть получена из дифференциального уравнения

или

где , после замены оператора дифференцирования p на оператор Лапласа s и деления полученного уравнения на .

В связи с тем что изображение δ-функции

изображение при нулевых начальных условиях уравнения

будет

,

где

.

Применив формулу обращения, получим

;

здесь c – абсцисса абсолютной сходимости интеграла.

Таким образом, оригиналом передаточной функции является импульсная характеристика усилителя.

Когда требуется определить частотные характеристики, то переходят от преобразования Лапласа к преобразованию Фурье, положив

,

где амплитудно-частотная характеристика

.

Пусть, например, передаточная функция имеет вид

.

следовательно, найдем АЧХ

.

Анализ последнего выражения показывает, что даже при всех положительных коэффициентах АЧХ может обратиться в бесконечность, если оба выражения, стоящие в круглых скобках знаменателя, обратятся в нуль. Это означает несходимость интеграла

,

обусловленную не затухающей с течением времени реакцией устройства на δ-функцию.

В таких случаях говорят, что работа устройства неустойчива и в нем возникли колебания выходного напряжения (тока). Так как колебания существуют без внешнего воздействия, то их называют автоколебаниями.

Если мнимые корни находятся в правой полуплоскости , то неустойчивость сохраняется, а при нахождении в левой полуплоскости – происходит затухание колебаний. Необходимые и достаточные условия отрицательности всех вещественных частей корней уравнения n-й степени с постоянными вещественными коэффициентами были даны Гурвицем (критерий устойчивости Гурвица, а также Михайлова и др.).

Устойчивость динамических систем

По определению, линейная динамическая система называется устойчивой, если все ее собственные колебания затухают во времени. Необходимым и достаточным условием устойчивости системы является отрицательность вещественных частей всех корней характеристического уравнения (8.36).

Эти корни не должны быть также и чисто мнимыми. Хотя при этом собственные колебания есть гармонические функции вида

небольшие случайные изменения параметров системы могут привести к переходу ее в неустойчивый режим, когда

представляют собой экспоненциально нарастающие по амплитуде колебания.

Если порядок динамической системы достаточно высок, то прямая проверка устойчивости, основанная на поиске корней характеристического уравнения, может оказаться весьма затруднительной. Поэтому были разработаны специальные критерии устойчивости, позволяющие определять наличие корней с положительными вещественными частями непосредственно по виду коэффициентов, минуя само решение характеристического уравнения (см. гл. 14).

Возникновение нарастающих собственных колебаний в электрических цепях возможно лишь тогда, когда в составе цепи, помимо пассивных элементов L, С, R, содержатся активные элементы, передающие в цепь часть энергии от внешних источников. Распространенной моделью такого активного элемента служит резистор с отрицательным сопротивлением.

Методы анализа прохождения радиотехнических сигналов через линейные стационарные системы во временной и спектральной области

Анализ во временной области

Импульсная характеристика

Пусть некоторая линейная стационарная система описывается оператором Т. Для простоты будем полагать, что входной и выходной сигналы одномерны. По определению, импульсной характеристикой системы называется функция h(t), являющаяся откликом системы на входной сигнал δ(t). Это означает, что функция h(t) удовлетворяет уравнению

. (5)

Поскольку система стационарна, аналогичное уравнение будет и в случае, если входное воздействие смещено во времени на производную величину t₀:

(6)

Следует ясно представить себе, что импульсная характеристика, так же как и порождающая ее дельта-функция, есть результат разумной идеализации. С физической точки зрения импульсная характеристика приближенно отображает реакцию системы на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временным масштабом системы, например периодом ее собственных колебаний.

Интеграл наложения. Зная импульсную характеристику линейной стационарной системы, можно формально решить любую задачу о прохождении детерминированного сигнала через такую систему. Входной сигнал всегда допускает представление вида

.

Отвечающая ему выходная реакция

(7)

Теперь примем во внимание, что интеграл есть предельное значение суммы, поэтому линейный оператор Т на основании принципа суперпозиции может быть внесен под знак интеграла. Далее, оператор Т «действует» лишь на величины, зависящие от текущего времени t, но не от переменной интегрирования τ. Поэтому из выражения (7) следует, что

,

или окончательно

(8)

Эта формула, имеющая фундаментальное значение в теории линейных систем, называется интегралом Дюамеля. Соотношение (8) свидетельствует о том, что выходной сигнал линейной стационарной системы представляет собой свертку двух функций — входного сигнала и импульсной характеристики системы. Очевидно, формула (8.8) может быть записана также в виде

(9)

Итак, если импульсная характеристика h(t) известна, то дальнейшие этапы решения сводятся к полностью формализованным операциям.

Легко видеть, что для физически реализуемой системы верхний предел в формуле интеграла Дюамеля может быть заменен на текущее значение времени:

(13)

Формула (13) имеет ясный физический смысл: линейная стационарная система, выполняя обработку поступающего на вход сигнала, проводит операцию взвешенного суммирования всех его мгновенных значений, существовавших «в прошлом» при — ∞ < τ < t. Роль весовой функции выполняет при этом импульсная характеристика системы. Принципиально важно, что физически реализуемая система, ни при каких обстоятельствах не способна оперировать «будущими» значениями входного сигнала.

Такие системы полезны при обработке сигналов, для которых в качестве независимой переменной выступает время, поскольку указанное ограничение физически обосновано и к тому же позволяет создавать системы, работающие в реальном масштабе времени.

Если сигнал представлен дискретными отсчетами, то (9) можно записать в следующем виде

если произвести замену , то выражение дискретной свертки можно записать в следующем виде

Например, для двумерная дискретная свертка

Импульсный отклик на произвольно расположенный входной импульс равен сдвинутому импульсному отклику на входной импульс, расположенный в начале координат.

Это соотношение известно под названием двумерной дискретной свертки.

ЛИС-система преобразует каждый импульс в сдвинутую копию импульсного отклика h(n₁, n₂). Суперпозиция этих взвешенных и сдвинутых импульсных откликов образует выходную последовательность, причем весовыми коэффициентами являются значения отсчетов входной последовательности х(n₁, n₂).

Выполнив замену переменных равенство () можно записать в другой форме:

(Зная импульсную характеристику линейной стационарной системы, можно формально решить любую задачу о прохождении детерминированного сигнала через такую систему. Входной сигнал всегда допускает представление вида

.

Отвечающая ему выходная реакция

(7)

Теперь примем во внимание, что интеграл есть предельное значение суммы, поэтому линейный оператор Т на основании принципа суперпозиции может быть внесен под знак интеграла. Далее, оператор Т «действует» лишь на величины, зависящие от текущего времени t, но не от переменной интегрирования τ. Поэтому из выражения (7) следует, что

,

или окончательно

(8)

Эта формула, имеющая фундаментальное значение в теории линейных систем, называется интегралом Дюамеля. Соотношение (8) свидетельствует о том, что выходной сигнал линейной стационарной системы представляет собой свертку двух функций — входного сигнала и импульсной характеристики системы.) – лишнее удалить.

Условие физической реализуемости (принцип казуальности). Каков бы ни был конкретный вид импульсной характеристики физически осуществимой системы(казуальной), всегда должен выполняться важнейший принцип: выходной сигнал, отвечающий импульсному входному воздействию, не может возникнуть до момента появления импульса на входе.

Отсюда вытекает очень простое ограничение на вид допустимых импульсных характеристик:

при t<0. (12)

Для большинства двумерных систем независимые переменные не связаны с временем, и казуальность не является естественным ограничением для таких систем. Однако при рассмотрении реализации систем мы вынуждены обратиться к обобщению понятия физически реализуемой системы.

Импульсный отклик h (n) физически реализуемой одномерной ЛИС-системы равен нулю при n<0. Соответственно обобщением понятия физической реализуемости может быть требование, чтобы импульсный отклик был равен нулю вне некоторой опорной области.

Рис. 3. а — последовательность с опорной областью в виде сектора; б — последовательность с опорной областью в виде квадранта, полученная из последовательности а путем линейного преобразования переменных при значениях(ЛГ,,,ЛГ₂₁) = (2,1) и (ЛГ«,N_a) = = (1,2); маленькие кружки обозначают отсчеты с нулевыми значениями.

Условие устойчивости физической системы. Физически реализуемая система должна быть, кроме того, устойчивой, представляют интерес лишь устойчивые системы. Естественно, например, потребовать, чтобы при ограниченной входной последовательности выходная последовательность была также ограничена. Чтобы отличить этот тип устойчивости от других, будем называть такие системы системами с ограниченными входом и выходом (ОВВ-системами). Необходимым и достаточным условием принадлежности ЛС-системы к классу ОВВ-систем является абсолютная суммируемость ее импульсного отклика

. (14)

Многомерная устойчивость значительно сложнее одномерной и для понимания, и с точки зрения испытаний системы на устойчивость.

Свойства свертки

Будем использовать одиночная звездочка (*) для обозначения одномерную свертки, двойная звездочка (* *) будет обозначать двумерную свертку.

Одним из достоинств линейных инвариантных к сдвигу систем является простота анализа соединенных друг с другом систем.

Частично это связано со свойствами оператора свертки. Мы уже видели, что свертка обладает свойством коммутативности:

у = х**h = h**х.

Свертка обладает также свойством ассоциативности. Если результат свертки х и h свернуть с g, результат будет тем же, что и при свертке х с результатом свертки h и g:

(х ** h) ** g = х ** (h ** g).

В силу свойства ассоциативности при описании многократной свертки скобки можно опускать.

Наконец, свертка обладает свойством дистрибутивности по отношению к операции сложения

х**(h + g) = (x**h) + (x**g).

Ассоциативные и дистрибутивные свойства оператора свертки достаточно наглядны. Две системы считаются соединенными последовательно, или каскадно, если выходной сигнал первой системы служит входным сигналом для второй, как это показано на рис. 1.

Если две системы линейны и инвариантны к сдвигу, то, как можно показать, их каскадное соединение также линейно и инвариантно к сдвигу. Если w обозначает выходной сигнал первой системы каскада, то

w = х * * h,

у = w ** g = (х ** h) ** g.

С учетом свойства ассоциативности выражение (1.49) можно переписать следующим образом:

у = х**(h ** g).

Рис.1. -Каскадное соединение двух систем.

Если обе системы линейны и инвариантны к сдвигу, порядок систем в каскаде не имеет значения, и с точки зрения преобразования входного сигнала в выходной обе схемы эквивалентны.

Отсюда эквивалентный импульсный отклик каскадной системы hэкв имеет вид

hэкв = h ** g.

Продвинувшись еще на шаг и использовав правило коммутативности, получим, что эквивалентный импульсный отклик не изменяется, если системы в каскаде поменять местами. Таким образом, две каскадные ЛИС-системы, которые отличаются только порядком входящих в них подсистем, а в остальном идентичны, являются эквивалентными; они формируют одинаковые выходные сигналы при возбуждении одним и тем же входным сигналом.

На рис. 2 показаны две системы, соединенные параллельно. У них общий вход, и общий выходной сигнал формируется путем суммирования выходных сигналов систем. Можно непосредственно доказать, что если обе эти системы линейны и инвариантны к сдвигу, то вся система в целом также линейна и инвариантна к сдвигу. Для нахождения эквивалентного импульсного отклика заметим, что

у = (х** р) + (х**g).

Применив правило дистрибутивности,получим

y = х**(h + g),

откуда следует, что

h_ЭKB = h + g.

Это правило очевидным образом обобщается на параллельное соединение более двух ЛИС-систем.

Рис. 2. - Параллельное соединение двух систем

Иногда оказывается полезным разложить импульсный отклик на несколько компонент, в частности если импульсный отклик имеет хотя и ограниченную, но причудливой формы опорную область, которую можно представить комбинацией меньших по размеру областей более правильной формы. В этом случае входную последовательность можно свернуть с импульсными откликами — компонентами и получить искомую выходную последовательность (суммируя результаты). В результате путем параллельного соединения более простых систем образуется интересующая нас система.

Переходная характеристика

Пусть на входе линейной стационарной системы действует сигнал, изображаемый функцией Хевисайда σ(t).

Выходную реакцию

(15)

принято называть переходной характеристикой системы. Поскольку система стационарна, переходная характеристика инвариантна относительно временного сдвига:

.

Высказанные ранее соображения о физической реализуемости системы полностью переносятся на случай, когда система возбуждается не дельта-функцией, а единичным скачком. Поэтому переходная характеристика физически реализуемой системы отлична от нуля лишь при t >=0, в то время как g(t)=0 при t < 0.

Между импульсной и переходной характеристиками имеется тесная связь. Действительно, так как

, то на основании (5)

Оператор дифференцирования d/dt и линейный стационарный оператор Т могут меняться местами, поэтому

(16)

Интеграл Дюамеля

Спектральный анализ

Частотный коэффициент передачи

При математическом исследовании систем особый интерес представляют такие входные сигналы, которые, будучи преобразованы системой, остаются неизменными по форме. Если имеется равенство

, (8.19)

то u_BX(t) является собственной функцией системного оператора Т, а число λ, в общем случае комплексное,— его собственным значением.

Комплексный сигнал при любом значении частоты ω есть собственная функция линейного стационарного оператора. Для этого воспользуемся интегралом Дюамеля вида (9) и вычислим

(20)

Отсюда видно, что собственным значением системного оператора является комплексное число

(21)

называемое частотным коэффициентом передачи системы.

Формула (21) устанавливает принципиально важный факт — частотный коэффициент передачи и импульсная характеристика линейной стационарной системы связаны между собой преобразованием Фурье.

Поэтому всегда, зная функцию K(jw), можно определить импульсную характеристику

(22)

Мы подошли к важнейшему положению теории линейных стационарных систем — любую такую систему можно рассматривать либо во временной области с помощью ее импульсной или переходной характеристик, либо в частотной области, задавая частотный коэффициент передачи. Оба подхода равноценны и выбор одного из них диктуется удобствами получения исходных данных о системе и простотой вычислений.

Частотный коэффициент передачи. Если на вход линейной динамической системы поступает сигнал, имеющий комплексную математическую модель вида

,

то сигнал на выходе

.

Подставляя эти выражения в (*), после сокращения на общий множитель находим частотный коэффициент передачи системы:

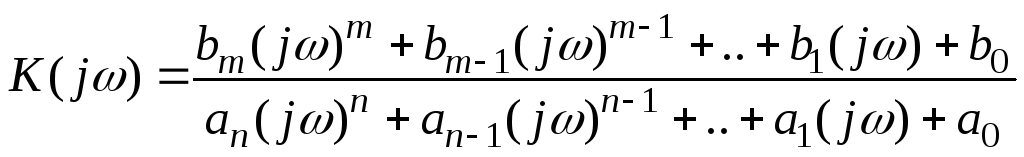
Итак, частотный коэффициент передачи любой динамической системы, описываемой обыкновенными дифференциальными уравнениями с постоянными коэффициентами, представляет собой дробно-рациональную функцию переменной jω; коэффициенты этой функции совпадают с коэффициентами дифференциального уравнения.

В инженерных расчетах частотный коэффициент передачи линейных систем часто находят методами теории цепей на основании принципиальных схем, не прибегая к составлению дифференциальных уравнений. Рассмотрим некоторые примеры.

Амплитудно-частотная и фазочастотная характеристики. Функция имеет простую интерпретацию: если на вход системы поступает гармонический сигнал с известной частотой ω и комплексной амплитудой , то комплексная амплитуда выходного сигнала

(24)

Часто пользуются представлением частотного коэффициента передачи в показательной форме:

(25)

Обе входящие сюда вещественные функции носят специальные названия: — амплитудно-частотная характеристика (АЧХ), — фазочастотная характеристика (ФЧХ) системы.

Рассмотрим двумерную ЛИС-системы с частотный коэффициент передачи системы (частотная характеристика или частотный отклик системы) и входным сигналом, представляющим собой комплексную синусоиду вида

где w1 и w2 — вещественные числа, называемые горизонтальной и вертикальной пространственными частотами соответственно. Выходной сигнал представляет собой комплексную синусоиду с теми же частотами, что и у входного сигнала, но с измененными амплитудой и фазой за счет комплексного множителя .

Можно показать, что частотный отклик периодичен с периодом 2π по обеим (горизонтальной и вертикальной) частотным переменным

В предыдущем разделе было показано, что для получения отклика двумерной ЛИС-системы на входной сигнал необходимо выполнить операцию свертки входного сигнала с импульсным откликом системы. Если представить входной сигнал в виде суперпозиции сдвинутых импульсов, то и выходной сигнал можно представить как суперпозицию сдвинутых импульсных откликов. Представление ЛИС-систем в частотной области также использует принцип суперпозиции, однако в этом случае элементарные последовательности являются комплексными синусоидами.

Ограничения, накладываемые на частотный коэффициент передачи. Далеко не каждая функция может являться частотным коэффициентом передачи физически реализуемой системы. Простейшее ограничение связано с тем, что импульсная характеристика h (t) такой системы обязана быть вещественной. В силу свойств преобразования Фурье (см. гл. 2) это означает, что

(26)

В соответствии с формулой (26) модуль частотного коэффициента передачи (АЧХ) есть четная, а фазовый угол (ФЧХ) — нечетная функция частоты.

Гораздо сложнее ответить на вопрос о том, каким должен быть частотный коэффициент передачи для того, чтобы выполнялись условия физической реализуемости (8.12) и (8.14). Приведем без доказательства окончательный результат, известный под названием критерия Пэли — Винера: частотный коэффициент передачи физически реализуемой системы должен быть таким, чтобы существовал интеграл

.

Фазовый сдвиг и групповое время задержки

Спектральный метод

Говоря о спектральном методе анализа прохождения, радиотехнических сигналов через линейные стационарные системы, обычно имеют в виду целый комплекс математических приемов, в основе которых лежит использование свойств частотного коэффициента передачи системы. Ниже на конкретных примерах показано применение спектрального подхода как к задаче нахождения реакции системы, так и к проблеме числовой оценки выходного сигнала.

Основная формула. Пусть на входе некоторой линейной стационарной системы действует детерминированный сигнал , заданный обратным преобразованием Фурье:

.

Будем полагать, что известен частотный коэффициент передачи К(jω) системы. Как было доказано, комплексный сигнал вида exp(jωt), являясь собственной функцией системного оператора, создает на выходе элементарную реакцию К(jω)exp(jωt). Суммируя эти реакции, находим представление выходного сигнала:

(8.48)

Получена основная формула спектрального метода, свидетельствующая о том, что частотный коэффициент передачи системы служит множителем пропорциональности между спектральными плотностями сигналов на входе и выходе:

(8.49)

Итак, анализ систем в частотной области отличается замечательной чертой — эффект преобразования сигнала в системе отображается просто алгебраической операцией умножения.

Следует иметь в виду, что спектральный и временной подходы полностью эквивалентны друг другу. Действительно, интеграл Дюамеля (8.8) есть свертка функции и импульсной характеристики h(t) во временной области:

.

Значит, спектральная плотность выходного сигнала есть произведение спектральных плотностей функций и h(t). Отсюда непосредственно следует формула (8.49).

Практическая ценность спектрального метода нахождения выходной реакции в каждом конкретном случае зависит от того, удается ли провести интегрирование в формуле (8.48).

Пример. Частотный коэффициент передачи напряжения RC-цепи, схема которой приведена в примере 8.7.

Здесь

где τ = RС-постоянная времени.

Уравнение АЧХ принимает вид

ФЧХ определяется следующим образом:

Вид АЧХ указывает на то, что такая цепь может использоваться в качестве фильтра нижних частот (ФНЧ).

Пример 8.12. Частотный коэффициент передачи напряжения Г-образного четырехполюсника, собранного из элементов L, С, R:

и уравнение ФЧХ

Если сопротивление потерь R достаточно мало, так что добротность системы, то данная цепь может с успехом выполнять роль полосового фильтра.

Дискретные системы