
- •Введение
- •Структура курса
- •Литература
- •Сигналы
- •Свойства сигналов
- •Случайные величины и процессы
- •Классификация свойств сигналов
- •Синусно-косинусная форма
- •Вещественная форма
- •Комплексная форма
- •Примеры расчета преобразования Фурье Прямоугольный импульс
- •Свойства преобразования Фурье
- •Представление непрерывных (аналоговых) сигналов в дискретной форме
- •Многомерное дискретное преобразование Фурье
- •Дпф произведения последовательностей
- •Круговая свертка
- •Спектральный анализ
- •Исследование спектра дискретного случайного процесса
- •Связь дпф и спектра дискретного сигнала
- •Растекание спектра
- •Весовые функции
- •Алгоритм быстрого преобразования Фурье
- •Бпф с прореживанием по времени
- •Бпф с прореживанием по частоте
- •Системы обработки сигналов
- •Реализация дискретных систем
- •Взаимосвязь дпф и фильтрации
- •Дпф как дискретная фильтрация
- •Проектирование дискретных фильтров
- •Синтез фильтров по аналоговому прототипу
- •Оптимальные методы
- •Восстановление сигналов (решение обратной задачи)
- •Шум квантования
- •И выбор структуры цифровых фильтров
- •4.6. Свойства цф различной структуры
- •Формы реализации дискретных фильтров
Шум квантования
При проектировании ЦФ в ряде случаев следует учитывать специфические погрешности их работы, возникающие за счет квантования сигналов, т. е. вследствие представления всех величин, как постоянных, так и изменяющихся во времени, в виде двоичных чисел с конечной разрядностью.
Квантованный характер сигналов приводит к целому ряду явлений. Рассмотрим простейший эффект - возникновение так называемого шума квантования.
Пусть umax — наибольшее значение аналогового сигнала на входе АЦП, которое еще не вызывает переполнения арифметических устройств фильтра. Если m - число двоичных разрядов, отводимых для представления чисел в фильтре, то очевидно, что квантование сигнала происходит с шагом
![]()
Квантованные
отсчеты описывают мгновенные значения
аналогового сигнала не точно, а с
некоторой погрешностью, тем меньшей,
чем меньше шаг квантования. Иными
словами, отсчеты входного сигнала
![]() фильтра являются суммами истинных
значений
фильтра являются суммами истинных
значений
![]() и отсчетов
и отсчетов
![]() некоторого дискретного случайного
процесса, называемого шумом квантования:
некоторого дискретного случайного
процесса, называемого шумом квантования:
![]()
Теоретически и экспериментально показано, что в большинстве случаев, интересных для практики, последовательность {nk} образована статистически независимыми случайными величинами, каждая из которых равномерно распределена на интервале от —qкв/2 до qкв/2 и поэтому имеет нулевое математическое ожидание и дисперсию
![]() .
.
Шум квантования, присутствующий на входе ЦФ, преобразуется этим устройством.. Для того чтобы найти отсчеты выходной последовательности шума квантования, следует вычислить дискретную свертку входного шумового сигнала и импульсной характеристики фильтра.
![]()
Таким образом, выходной шум квантования оказывается тем больше, чем медленнее уменьшаются отсчеты импульсной характеристики фильтра.
Квантование коэффициентов цифровых фильтров
Получая коэффициенты фильтров некоторыми расчетными методами, считали, что они представлены точно. Однако при практической реализации фильтров почти неизбежно возникает необходимость округления их коэффициентов. При использовании цифровых сигнальных процессоров это связано с поддерживаемыми ими форматами представления чисел, при создании программ обработки сигналов для персональных компьютеров — со стремлением повысить быстродействие.
Из-за округления коэффициентов характеристики фильтра претерпевают искажения, величина которых зависит не только от погрешности представления коэффициентов, но и от исходных параметров фильтра и формы его построения (см. раздел «Формы реализации дискретных фильтров» главы 4).
В нерекурсивных фильтрах коэффициенты равны отсчетам импульсной характеристики и линейно связаны с комплексным коэффициентом передачи. Поэтому малые искажения коэффициентов приводят к малым искажениям частотных характеристик и проблемы, связанные с округлением коэффициентов, проявляются редко. Однако, если фильтр должен иметь очень крутой спад АЧХ между полосами пропускания и задерживания, округление коэффициентов все же может привести к заметным искажениям частотных характеристик.
Убедимся в этом на простом примере. Синтезируем методом Ремеза ФНЧ 256-го порядка с полосой пропускания, простирающейся до 0,2, и полосой задерживания, начинающейся от 0,21 (указаны частоты, нормированные к частоте Найквиста). Затем округлим коэффициенты фильтра с точностью до 1/256, оставив в них 8 двоичных разрядов после запятой, и построим графики АЧХ до и после округления (рис. 7.3):

Как видите, ничего особенно страшного не произошло — лишь увеличился размах пульсаций АЧХ. Естественно, в любом случае следует обязательно проконтролировать параметры фильтра после округления коэффициентов, чтобы проверить, удовлетворяет ли квантованный фильтр предъявляемым к нему требованиям.
Значительно серьезнее сказывается округление коэффициентов на характеристиках рекурсивных фильтров, поскольку коэффициенты знаменателя функции передачи связаны с импульсной и частотными характеристиками нелинейно. Как правило, наибольшие искажения происходят в тех случаях, когда АЧХ фильтра имеет крутые скаты в переходных зонах между полосами пропускания и задерживания.
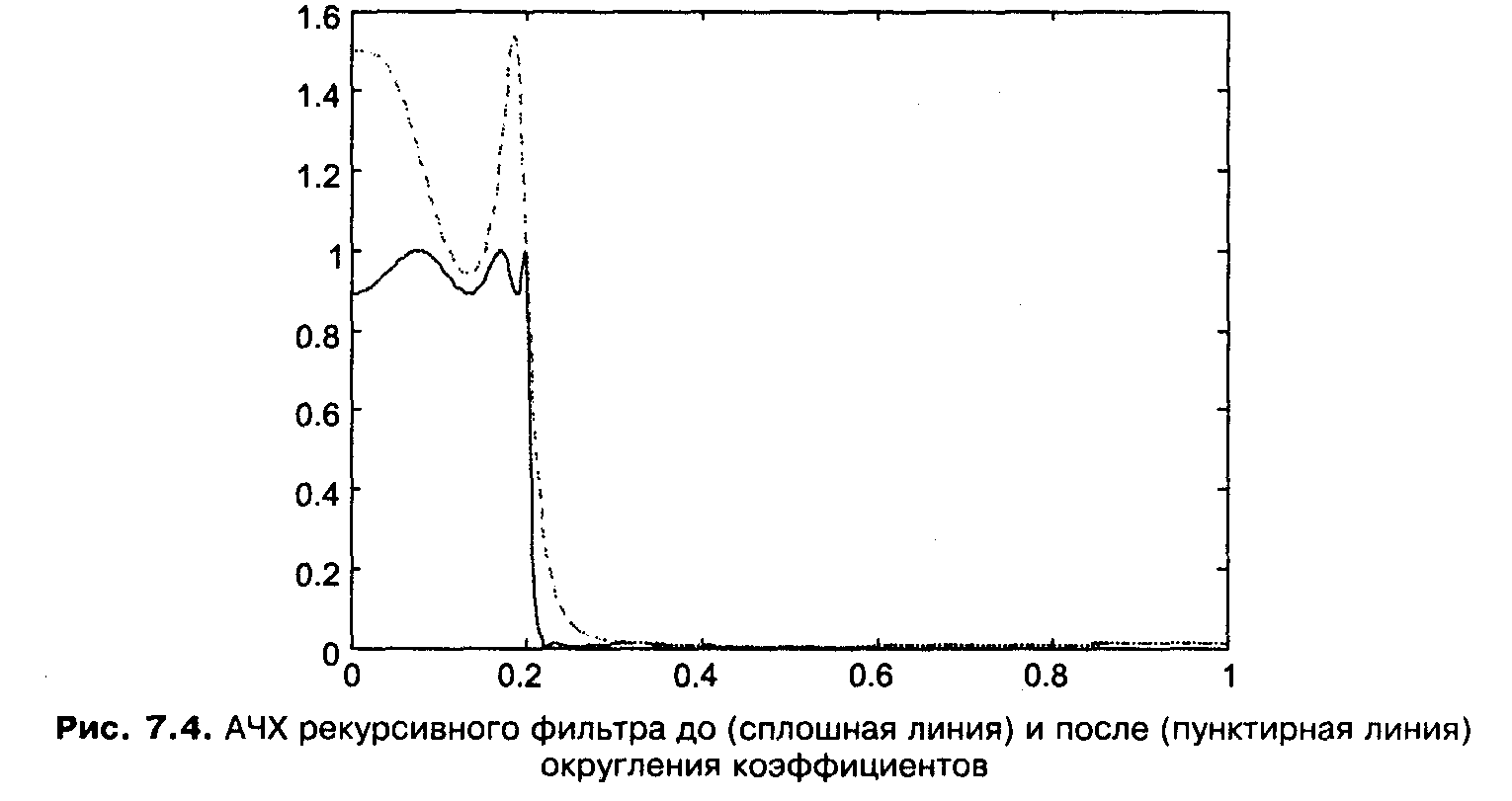
Приведём пример, иллюстрирующий сказанное. Рассчитаем эллиптический ФНЧ 6-го порядка, имеющий частоту среза, составляющую 0,2 от частоты Найквиста, пульсации в полосе пропускания, равные 1 дБ, и уровень пульсаций в полосе задерживания, равный —40 дБ. Напомним, что из всех фильтров, синтезируемых по аналоговым прототипам, именно эллиптические фильтры дают максимальную крутизну спада АЧХ при переходе от полосы пропускания к полосе задерживания. Далее округляем коэффициенты фильтра точно так же, как это делалось в предыдущем примере, и строим графики АЧХ фильтра до и после округления (рис. 7.4):
В данном случае АЧХ изменилась просто катастрофически: в несколько раз увеличилась амплитуда пульсаций коэффициента передачи в полосе пропускания, скат АЧХ стал заметно более пологим, в полосе задерживания исчезли две точки с нулевым коэффициентом передачи.
Теперь посмотрим, что изменится, если мы представим исходный фильтр по-другому — в виде трех последовательно включенных секций второго порядка. В данном случае разница между АЧХ исходного и квантованного фильтра настолько мала, что визуально она не проявляется. Поэтому вместо графиков самих АЧХ построим график их разности (рис. 7.5):
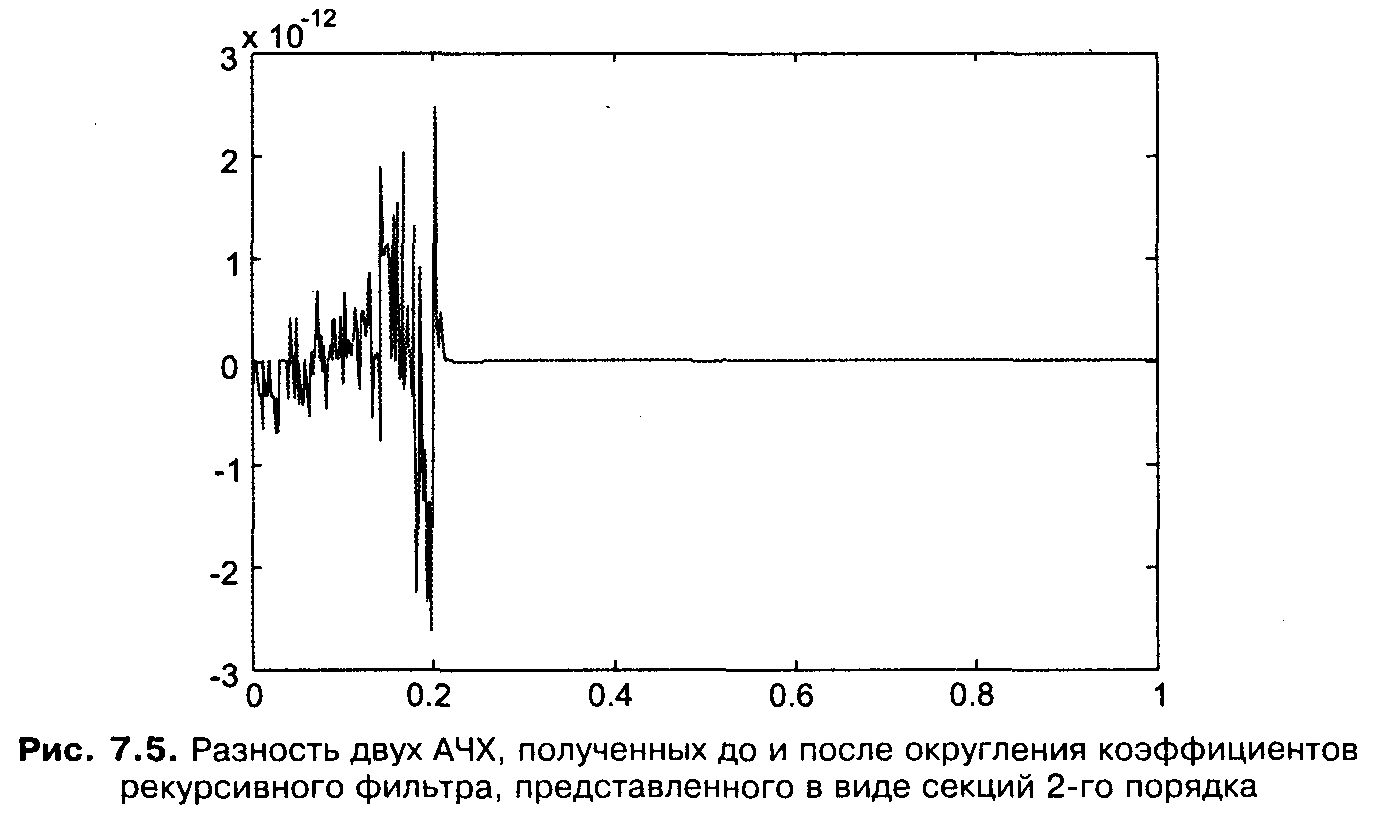
Рисунок
7.5 показывает, что отклонение АЧХ
квантованного фильтра от исходной не
превосходит
![]() ,
то есть весьма невелико. Таким образом,
при представлении фильтра в виде
последовательно включенных секций
второго порядка округление коэффициентов
влияет на характеристики фильтра
значительно слабее, чем при прямой форме
реализации.
,
то есть весьма невелико. Таким образом,
при представлении фильтра в виде
последовательно включенных секций
второго порядка округление коэффициентов
влияет на характеристики фильтра
значительно слабее, чем при прямой форме
реализации.
Данный пример демонстрирует общую закономерность, впервые установленную Кайзером [8]: параметры любого фильтра с резким изменением частотной характеристики в переходной полосе, реализованного в прямой форме, крайне чувствительны к значениям коэффициентов фильтра.
Существует два основных подхода к анализу и синтезу фильтров с квантованными коэффициентами.
Можно рассматривать погрешности представления коэффициентов как случайные величины и, задав статистическое описание этих погрешностей, оценить среднеквадратическое отклонение частотной характеристики от исходной.
Второй подход заключается в использовании прямой оптимизации квантованных коэффициентов с целью достижения минимального (в смысле среднеквадратической ошибки или максимального модуля разности) отклонения АЧХ от заданной.
Масштабирование коэффициентов цифровых фильтров
При разработке систем, работающих в реальном масштабе времени, для ускорения вычислений часто используется формат с фиксированной запятой. В этом случае может оказаться, что значения некоторых коэффициентов фильтров выходят за пределы диапазона, представимого в выбранном формате. Для решения данной проблемы прибегают к масштабированию фильтров. Наиболее часто коэффициенты приводят к диапазону [-1, 1]. При масштабировании цифрового фильтра все его коэффициенты делятся на одну и ту же константу, и на нее же умножается рассчитанный выходной сигнал. В качестве масштабирующего множителя удобно выбирать степень двойки, поскольку умножение на степень двойки в формате с фиксированной запятой сводится к поразрядному сдвигу двоичного представления числа влево.
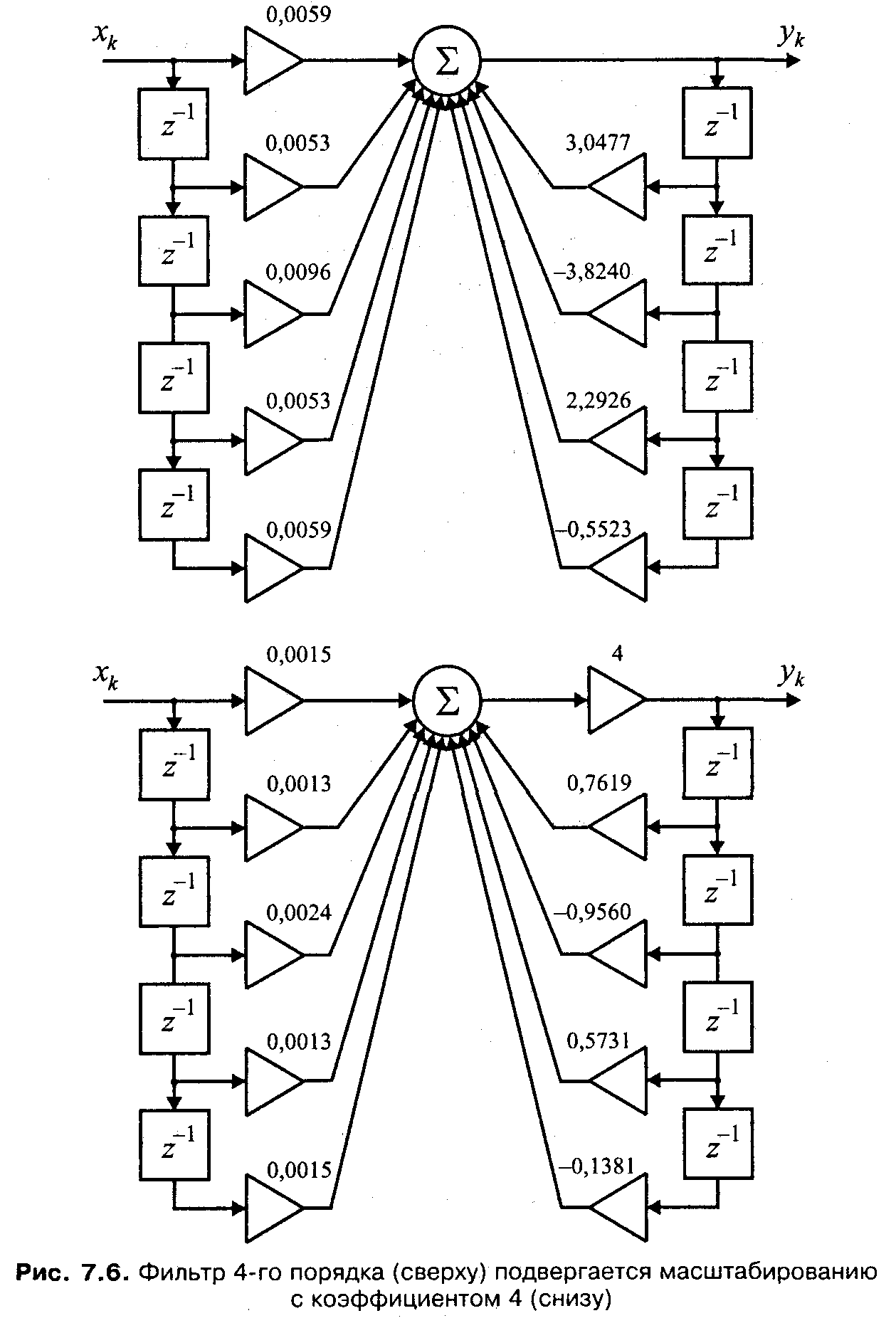
Если фильтр высокого порядка реализуется «целиком» (без разделения его на последовательно включенные секции), диапазон абсолютных значений коэффициентов фильтра может быть весьма широк. При представлении коэффициентов в формате с фиксированной запятой оказывается, что самые маленькие (по модулю) коэффициенты могут из-за округления потерять несколько значащих цифр. Это приводит к искажению характеристик фильтра, порой весьма существенному, особенно в рекурсивных фильтрах. Данный эффект мы уже обсуждали в предыдущем разделе. Там же мы видели, что реализация фильтра в виде последовательно включенных секций второго порядка значительно ослабляет эти искажения. Это происходит из-за того, что в каждой отдельно взятой секции второго порядка разброс абсолютных значений коэффициентов оказывается значительно меньше, чем у фильтра в целом, особенно если при разбиении на секции группировать ближайшие друг к другу пары нулей и полюсов.
Переполнение разрядной сетки в процессе вычислений
В процессе вычисления выходного сигнала фильтра производится множество операций умножения и сложения. При этом промежуточные результаты вычислений могут значительно превосходить окончательное значение и вызвать переполнение разрядной сетки вычислительного устройства.
Переполнения в процессе вычислений могут стать серьезной проблемой при реализации алгоритмов цифровой обработки сигналов. Уменьшить вероятность переполнений можно, используя для хранения чисел формат с плавающей запятой, обладающий большим динамическим диапазоном, однако в этом случае возрастает сложность реализации арифметических операций. В любом случае разработанная система обработки сигналов должна тщательно тестироваться для обнаружения потенциальных проблем, связанных с конечной точностью вычислений. Различние формы реализации фильтров обладают различной степенью чувствительности к этому эффекту. Например, у канонической формы эффект выражен сильнее, чем в прямой форме(на порядок)
Округление промежуточных результатов вычислений
При реализации различных алгоритмов обработки сигналов в процессе вычислений формируется множество промежуточных результатов. Формат хранения этих результатов зачастую вынуждает округлять их, что приводит к появлению дополнительных погрешностей. Операции, при которых появляются эти погрешности, зависят от способа представления чисел, используемого в вычислительном устройстве.
При использовании арифметики с фиксированной запятой операции сложения и вычитания не приводят к необходимости округления результатов — они могут вызвать лишь переполнение.
А вот для представления целой части суммы нужно три разряда, тогда как для слагаемых было достаточно двух. Поэтому, если для представления целой части чисел используется два разряда, в данном случае возникнет переполнение.
В отличие от сложения умножение чисел с фиксированной запятой приводит к увеличению числа значащих цифр результата (по сравнению с сомножителями) и, следовательно, к необходимости округления.
Результат умножения в данном примере имеет 6 значащих цифр после запятой. Если для представления результата используется тот же формат, что и для сомножителей, придется производить округление:
11,10011100 ≈ 11,1010 3.609375 ≈ 3.625
Если для представления чисел используется формат с плавающей запятой, все сказанное об умножении сохраняет силу. Впрочем, если результат умножения по модулю не превосходит единицы, использование формата с плавающей запятой даст большую точность, поскольку не будут зря тратиться разряды для представления незначащих нулей слева.
Однако операции сложения в формате с плавающей запятой тоже могут приводить к потере точности. Пусть рассматриваемые нами два числа представлены в формате с плавающей запятой, использующем 6 разрядов для хранения дробной части нормализованной мантиссы (мантисса и порядок записаны в двоичной системе счисления):
При сложении чисел с плавающей запятой может не выполняться свойство ассоциативности — результат суммирования нескольких чисел может зависеть от последовательности выполнения сложений. При обучении программированию обычно дается рекомендация складывать числа, начиная с меньших (по модулю) и заканчивая самыми большими. Однако при реализации алгоритмов цифровой обработки сигналов мы, как правило, лишены возможности произвольно менять последовательность суммирования (хотя бы потому, что для сортировки слагаемых потребуется дополнительное время).
Для статистического анализа ошибок округления в структурную схему фильтра вводятся эквивалентные источники шума, добавляемого к результатам умножения и (при использовании арифметики с плавающей запятой) сложения. Более подробную информацию об этом можно найти в [8].
Примеры моделирования ошибок округления в цифровом фильтре и при расчете БПФ приведены при описании функций qfilt и qfft пакета Filter Design.
Предельные циклы
Ошибки округления при вычислениях в цифровых фильтрах могут приводить к еще одной очень серьезной неприятности — появлению так называемых предельных циклов (limit cycle), когда вроде бы устойчивый фильтр начинает демонстрировать неустойчивое поведение.
Поясним это явление на простейшем примере, взятом из [8]. Пусть имеется рекурсивный фильтр первого порядка, описываемый разностным уравнением
y(k) =x(k) + 0,95y(k - 1).
Единственный полюс функции передачи данного фильтра, равный 0,95, находится внутри единичной окружности, что свидетельствует об устойчивости фильтра. Пусть входной сигнал отсутствует (x(k) - 0), а внутреннее состояние фильтра, которое в данном случае представляется единственным числом y(0), равно 13. При точных вычислениях сигнал на выходе фильтра экспоненциально затухает:
y(l) = 0,95 y(0) = 0,95 • 13 = 12,35,
y(2) = 0,95 y(1) = 0,95 • 12,35 = 11,7325,
y(3) = 0,95 y(2) = 0,95 • 11,7325 = 11,145875,
y(4) = 0,95 y(3) = 0,95 • 11,145875 = 10,58858125,
y(5) = 0,95 y(4) = 0,95 • 10,58858125 = 10,0591521875,
…
А теперь будем считать, что в ячейке памяти фильтра значение хранится в целочисленном формате и после выполнения умножения используется округление (будем обозначать его квадратными скобками). Выходной сигнал радикально изменится:
у(1) = [0,95 y(0)] = [0,95 • 13] = [12,35] = 12,
y(2) = [0,95 у(1)] = [0,95 • 12] = [11,4] = 11,
y(3) = [0,95 y(2)] = [0,95 • 11] = [10,45] = 10,
y(4) = [0,95 y(3)] = [0,95 • 10] = [9,5] = 10,
y(5) = [0,95 y(4)] = [0,95 • 10] = [9,5] = 10,
…
Итак, выходной сигнал фильтра «залипает» на значении 10 и далее не меняется. Это и есть простейший случай предельного цикла (с периодом, равным единице).
Если в разностном уравнении фильтра изменить знак у коэффициента 0,95, мы получим предельный цикл с периодом, равным двум, в виде чередования значений 10 и -10. В фильтрах более высокого порядка могут возникать предельные циклы с разным периодом.
Различают две разновидности предельных циклов:
-
«зернистые» (granular) предельные циклы возникают, когда значения внутреннего состояния фильтра при отсутствии входного сигнала затухают, но из-за ошибок округления не доходят до нуля. Именно такой цикл наблюдается в приведенном примере;
-
«переполняющие» (overflow) предельные циклы имеют место в том случае, когда из-за вычислительных погрешностей значения внутреннего состояния фильтра при отсутствии входного сигнала не затухают, а возрастают, вызывая переполнение.
Для анализа возможностей возникновения предельных циклов используется понятие эффективных значений коэффициентов знаменателя функции передачи фильтра. Под эффективным значением коэффициента понимается отношение округленного результата умножения к использованному в качестве множителя значению внутреннего состояния фильтра. Эффективное значение коэффициента будет разным для разных значений состояния. Если для какого-то внутреннего состояния фильтра набор эффективных значений коэффициентов дает полюс функции передачи, расположенный на единичной окружности, это означает, что данное внутреннее состояние при отсутствии входного сигнала дает предельный цикл.
В нашем примере эффективное значение единственного коэффициента фильтра равно
![]() .
.
Построим график значений аэфф для целочисленных значений y(k — 1), лежащих в диапазоне от -20 до 20 (рис. 7.9):
Как видите, если y(k - 1) лежит в диапазоне от -10 до 10, значение a3,M, становится равным единице, а фильтр оказывается на границе устойчивости (полюс функции передачи лежит на единичной окружности), что и приводит к появлению предельного цикла.
В приведенном примере анализ предельных циклов оказывается очень простым, поскольку внутреннее состояние фильтра описывается единственным числом. Для фильтров, степень знаменателя функции передачи которых превышает единицу, анализ базируется на тех же принципах, но оказывается более сложным. Для выполнения такого анализа в пакете Filter Design имеется специальная функция limitcycle, которую мы рассмотрим далее в этой главе.

Алгоритм расчета масштабных множителей и разрядности
