Комплексная форма

Комплексная форма получается из вещественной формы представлением косинуса в виде полусуммы комплексных экспонент (такое представление вытекает из формулы Эйлера е^jx=cos(х) + j sin(x):

Применив данное преобразование к вещественной форме ряда Фурье, получим суммы комплексных экспонент с положительными и отрицательными показателями:

.

А теперь будем трактовать экспоненты со знаком «минус» в показателе как члены ряда с отрицательными номерами. В рамках этого же общего подхода постоянное слагаемое а₀/2 станет членом ряда с нулевым номером.

В результате получится комплексная форма записи ряда Фурье:

Комплексные коэффициенты ряда связаны с амплитудами А_k, и фазами φ_k, фигурирующими в вещественной форме записи ряда Фурье, следующими несложными соотношениями:

, , .

Напоминание: .

Несложно выглядят и формулы связи с коэффициентами а_k и b_k, синусно-косинусной формы ряда Фурье:

.

Отсюда сразу же следует и формула непосредственного расчета коэффициентов C_k ряда Фурье в комплексной форме:

.

Если s(t) является четной функцией, коэффициенты ряда C_k будут чисто вещественными, а если s(t) — функция нечетная, коэффициенты ряда окажутся чисто мнимыми.

Если анализируемый сигнал s(t) является вещественным, то его амплитудный и фазовый спектры обладают симметрией:

, ,

ЗАМЕЧАНИЕ -----------------------------------------------------------------------------------------

Отрицательная частота – понятие не физическое, а математическое, вытекающее из способа представления комплексных чисел. Положительной частоте соответствует вектор, вращающийся против часовой стрелки, а отрицательной частоте – вектор, вращающийся по часовой стрелке.

Рисунок

Преобразование Фурье

Преобразование Фурье (Fourier transform) является инструментом спектрального анализа непериодических сигналов.

Впрочем, чуть позже мы увидим, что его можно применять и к сигналам периодическим, но это потребует использования аппарата обобщенных функций.

Для наглядной иллюстрации перехода от ряда Фурье к преобразованию Фурье часто используется не вполне строгий математически, но зато понятный подход.

Представим себе периодическую последовательность импульсов произвольного вида и сформируем ряд Фурье для нее. Затем, не меняя формы одиночных импульсов, увеличим период их повторения (заполнив промежутки нулевым значением) и снова рассчитаем коэффициенты ряда Фурье.

Формула для расчета коэффициентов ряда показывает, что нам придется вычислить тот же самый интеграл, но для более тесно расположенных частот

Изменение пределов интегрирования не играет роли — ведь на добавившемся между импульсами пространстве сигнал имеет нулевое значение. Единственное дополнительное изменение будет состоять в уменьшении общего уровня гармоник из-за деления результата интегрирования на увеличившийся период Т.

На рисунке описанные изменения иллюстрируются на примере двукратного увеличения периода следования прямоугольных импульсов. Обратите внимание на то, что горизонтальная ось спектральных графиков проградуирована в значениях частот, а не номеров гармоник.

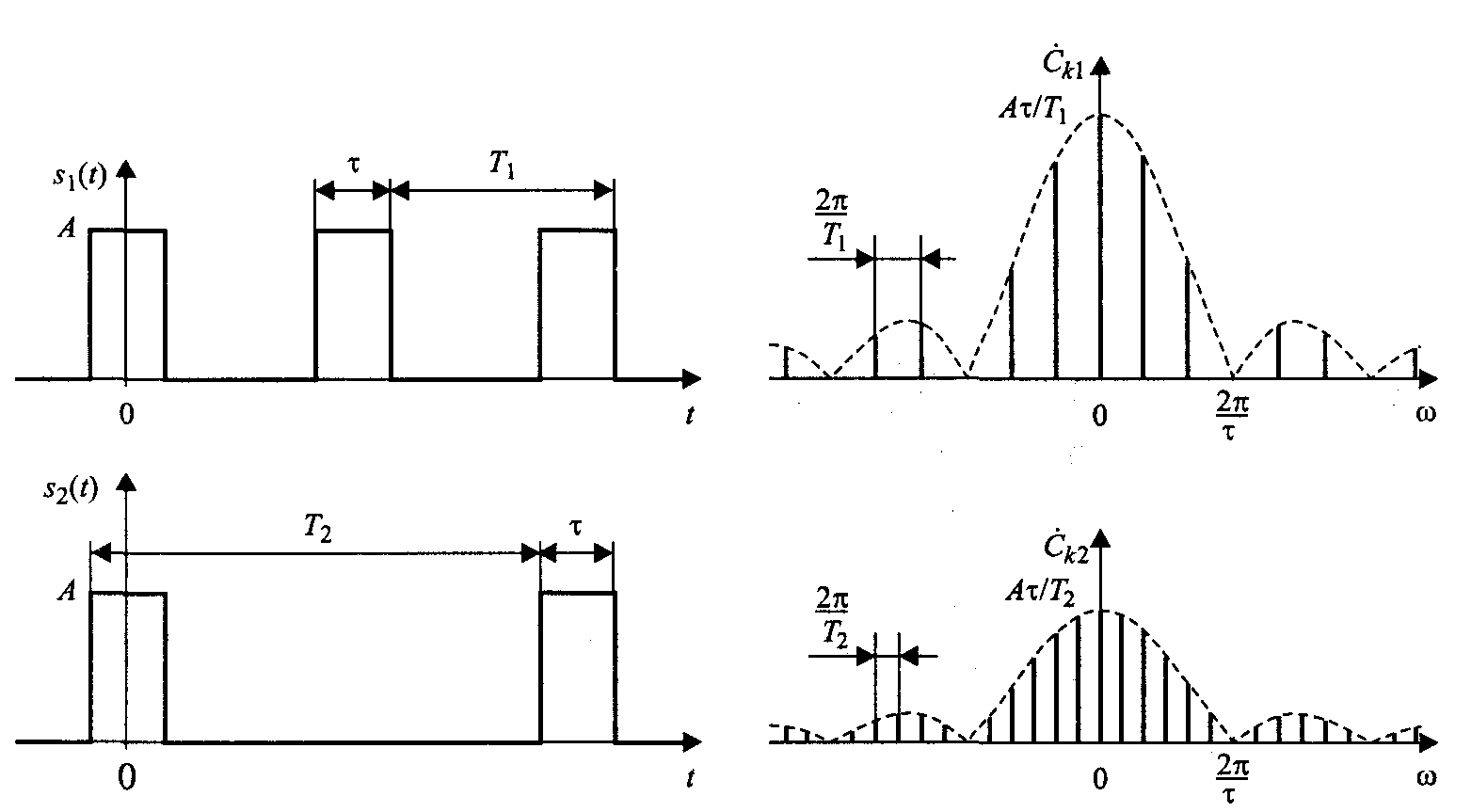
Рис. Изменение спектра последовательности импульсов при двукратном увеличении периода их следования

Итак, с ростом периода следования импульсов гармоники располагаются ближе друг к другу по частоте, а общий уровень спектральных составляющих становится все меньше. При этом вид вычисляемого интеграла не меняется.

Наконец, если устремить период к бесконечности (превратив тем самым периодическую последовательность в одиночный импульс), гармоники спектра будут плотно занимать всю частотную ось, а их амплитуды упадут до нуля (станут бесконечно малыми). Однако взаимное соотношение между уровнями гармоник остается неизменным и определяется все тем же интегралом.

Поэтому при спектральном анализе непериодических сигналов формула для расчета коэффициентов комплексного ряда Фурье модифицируется следующим образом:

- частота перестает быть дискретно меняющейся и становится непрерывным параметром преобразования (то есть в формуле заменяется на );

- удаляется множитель 1/T;

- результатом вычислений вместо нумерованных коэффициентов ряда C_k, является функция частоты S(ω) — спектральная функция сигнала s(t). Иногда ее называют также спектральной плотностью.

В результате перечисленных модификаций формула ( ) превращается в формулу прямого преобразования Фурье:

. ( )

В формуле самого ряда Фурье суммирование, естественно, заменяется интегрированием (и, кроме того, перед интегралом появляется деление на 2π). Получающееся выражение называется обратным преобразованием Фурье.

( )

ЗАМЕЧАНИЕ ---------------------------------------------------------------------------------------

Если использовать не круговую частоту ω, а обычную частот f=ω/(2π), формулы прямого и обратного преобразования Фурье становятся еще более симметричными, отличаясь лишь знаком в показателе экспоненты:

Чтобы преобразование Фурье было применимо, сигнал должен удовлетворять следующим требованиям:

- должны выполняться условия Дирихле (см. раздел «Ряд Фурье»);

- сигнал должен быть абсолютно интегрируемым. Это означает, что интеграл от его модуля должен быть конечной величиной:

Однако с привлечением математического аппарата обобщенных функций возможно выполнение Фурье-анализа и для некоторых сигналов, не удовлетворяющих этим требованиям (речь об этом пойдет далее, в разделе «Фурье-анализ неинтегрируемых сигналов»).

Если анализируемый сигнал s(t) — вещественная функция, то соответствующая спектральная функция является «сопряженно-симметричной» относительно нулевой частоты. Это означает, что значения спектральной функции на частотах ω и минус ω являются комплексно-сопряженными по отношению друг к другу:

.

Если s(t) — четная функция, то, как и в случае ряда Фурье, спектр будет чисто вещественным (и, следовательно, будет являться четной функцией). Если, напротив, s(t) — функция нечетная, то спектральная функция будет чисто мнимой (и нечетной).

Модуль спектральной функции часто называют амплитудным спектром, а ее аргумент — фазовым спектром. Легко показать, что для вещественного сигнала амплитудный спектр является четной, а фазовый — нечетной функцией частоты:

,

.

Итак, преобразование Фурье (1.11) ставит в соответствие сигналу, заданному во времени, его спектральную функцию. При этом осуществляется переход из временной области в частотную.

Преобразование Фурье является взаимно-однозначным, поэтому представление сигнала в частотной области (спектральная функция) содержит ровно столько же информации, сколько и исходный сигнал, заданный во временной области.