Связь дпф и спектра дискретного сигнала

Имея один и тот же конечный набор чисел, можно рассчитать либо спектральную функцию этого дискретного сигнала по формуле

(3.2),

либо его ДПФ по формуле

(5.3).

Разумеется, возникает вопрос о том, как связаны друг с другом эти два спектральных представления, полученные на основе одних и тех же отсчетов сигнала.

Сравнение формул (3.2) и (5.3) показывает, что ДПФ представляет собой просто дискретные отсчеты спектральной функции дискретного сигнала, соответствующие частотам :

. (5.12)

По этой причине значения ДПФ иногда называют спектральными отсчетами.

Из соотношения (5.12) следует еще один важный вывод: если добавить к конечному набору отсчетов некоторое количество нулей, спектральная функция дискретного сигнала, естественно, не изменится, но ДПФ даст большее число спектральных отсчетов, соответствующих частотам, более тесно расположенным в интервале от нуля до частоты дискретизации.

Поясним сказанное на простом примере, вычислив ДПФ для отсчетов прямоугольного импульса при разном количестве концевых нулей (рис. 5.1):

Рис. 5.1. Повышение спектрального разрешения ДПФ при дополнении сигнала нулями: сверху — исходный сигнал и модуль его ДПФ, снизу — сигнал, дополненный 16 нулями, и модуль его ДПФ

Растекание спектра

Как уже говорилось, при ДПФ предполагается, что последовательность отсчетов анализируемого сигнала является периодически продолженной вперед и назад во времени. При этом, если значения начальных и конечных отсчетов сигнала сильно различаются, при периодическом повторении на стыках сегментов возникают скачки, из-за которых спектр сигнала расширяется.

Это явление, называемое растеканием спектра (spectrum leakage), можно наглядно проиллюстрировать на простейшем примере вычисления спектра дискретного гармонического сигнала

(5.18)

Если анализируемая последовательность содержит целое число периодов гармонического сигнала (то есть если отношение является целым числом), то периодически продолженный сигнал представляет собой гармонические колебания (без скачков), а подстановка (5.18) в формулу ДПФ (5.3) показывает, что вычисленное ДПФ содержит лишь два спектральных отсчета, отличных от нуля:

.

Таким образом, аналогично спектру непрерывного гармонического сигнала, ДПФ отличается от нуля всего для двух значений п. Однако если отношение не является целым числом, спектр оказывается значительно более богатым. Этому можно дать простое объяснение: ведь в данном случае периодически продолженная последовательность уже не может являться набором отсчетов непрерывной синусоиды. Поэтому, в полном соответствии со свойствами преобразования Фурье, в спектре появляются дополнительные составляющие.

Построим графики дискретных сигналов, содержащих по 16 отсчетов гармонических сигналов с периодами, равными 4 отсчетам (периодически продолженный сигнал является периодическим, рис. 5.10 сверху) и 6 отсчетам (периодически продолженный сигнал содержит скачки, рис. 5.10 снизу), и покажем вид модуля их ДПФ:

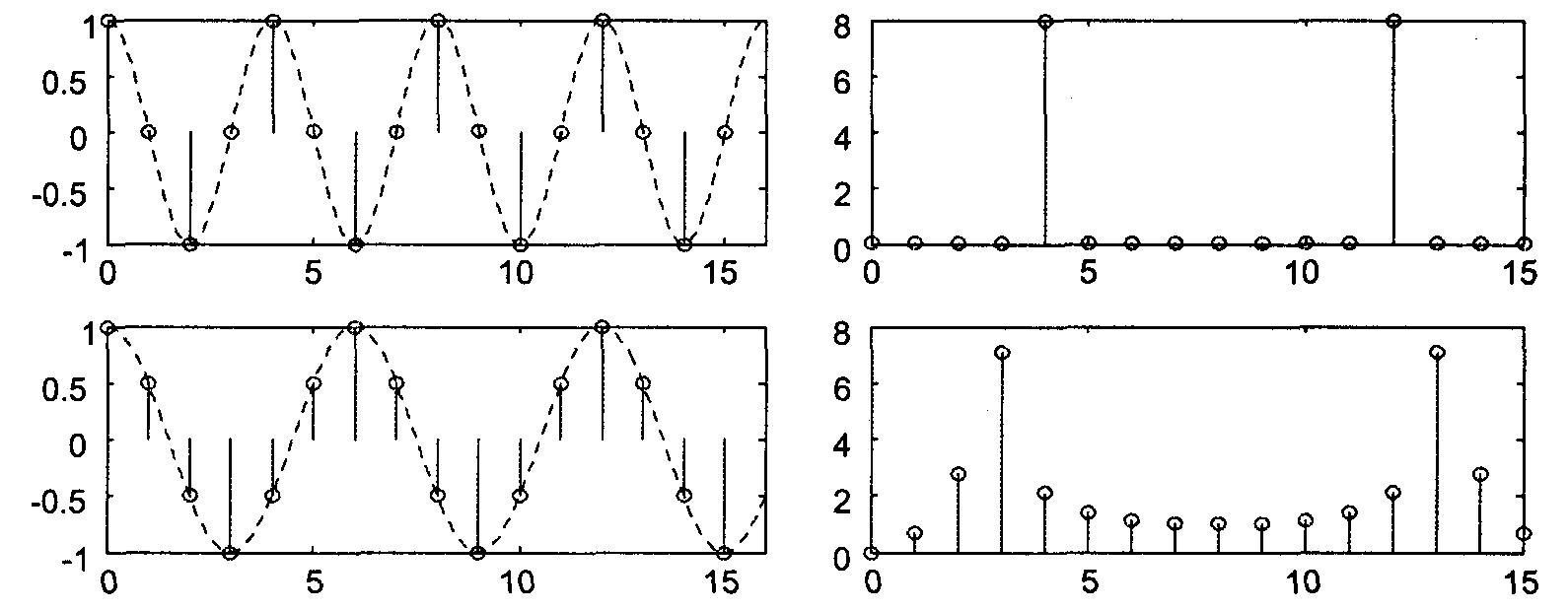
Рис. 5.10. Дискретное преобразование Фурье для целого (сверху) и нецелого (снизу) числа периодов гармонического сигнала (слева — исходные последовательности, справа — модули их ДПФ)

Необходимо подчеркнуть, что причиной растекания спектра является именно периодическое продолжение анализируемого сигнала. Спектр одиночного фрагмента дискретной синусоиды, в соответствии с тем, что говорилось в главе 3, является периодической непрерывной функцией частоты. Эта функция имеет лепестковую структуру независимо от того, целое или нецелое число периодов укладывается в анализируемом сегменте. Однако дискретный ряд частот, на которых вычисляется ДПФ, может быть по-разному расположен относительно лепестков спектральной функции. В случае целого числа периодов все анализируемые частоты (кроме двух) попадают как раз на границы между лепестками. При нецелом числе периодов такого не происходит. Для иллюстрации этого факта построим графики периодически продолженных сигналов, а также модулей их ДПФ и непрерывных амплитудных спектров одиночных фрагментов синусоиды (рис. 5.11):

Возможна еще одна трактовка причины растекания спектра. В этом случае мы не считаем анализируемый сигнал периодически продолженным, а предполагаем, что все содержащиеся в нем гармонические компоненты существуют и за пределами анализируемого фрагмента. Спектр такого сигнала представляет собой набор дельта-функций, а растекание спектра при ДПФ можно объяснить наличием боковых лепестков у АЧХ фильтров, соответствующих отдельным частотным каналам ДПФ (см. раздел «ДПФ как дискретная фильтрация», формулу (5.17) и рис. 5.6).

Рис. 5.11. Происхождение растекания спектра: слева — периодически продолженные сигналы, справа — амплитудные спектры одиночных сигналов (пунктирные линии) и модули ДПФ (кружочки)

ЗАМЕЧАНИЕ --------------------------------------------------------------------------------------

Аналогичные проблемы, связанные с наличием боковых лепестков у АЧХ фильтров, соответствующих отдельным частотным каналам ДПФ, возникают при использовании ДПФ для синтеза дискретных фильтров (см. далее раздел «Синтез с использованием окон» главы 6).