Оптимальные методы
Оптимальные методы, в которых численными итерационными методами ищется минимум заданной функции качества.
Чаще всего отправной точкой при расчете фильтра служит его желаемая частотная характеристика — либо АЧХ (когда фазовые характеристики не важны), либо комплексный коэффициент передачи. В качестве минимизируемой меры отклонения характеристики фильтра от заданной в общем случае используется р-норма ошибки. Такая норма Lp для функции f(x), определенной на интервале от a до b, рассчитывается следующим образом:
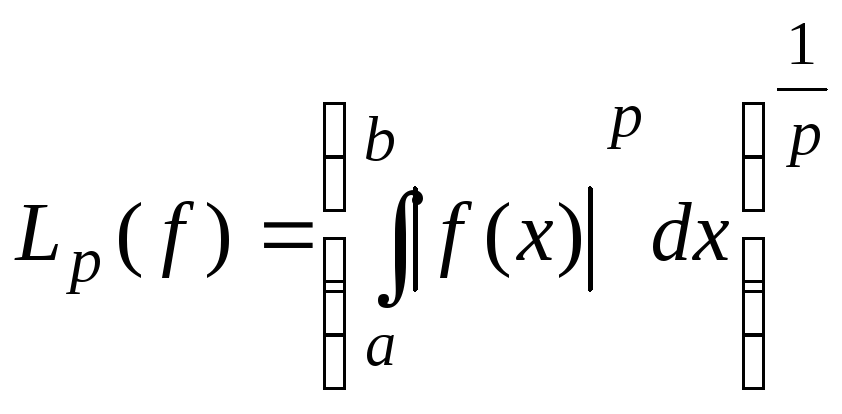
При р=2 норма L2 пропорциональна среднеквадратическому значению функции. При норма Lx дает максимальное (по модулю) значение функции, достигаемое на рассматриваемом интервале. При р=∞ рассматриваемая норма ошибки равна максимальному абсолютному отклонению характеристики от заданной. Минимизация этой нормы соответствует минимаксной аппроксимации (minimax approximation) и дает фильтры с равномерными пульсациями АЧХ (equiripple filter). Для минимаксного синтеза нерекурсивных фильтров используется метод чебышевской аппроксимации с использованием алгоритма многократной замены Ремеза.
Поскольку корень р-й степени при любом р является монотонно возрастающей функцией, при расчете минимизируемой величины его можно не вычислять.
Использование весовой функции позволяет придать разную значимость различным участкам частотной оси. В частности, это дает возможность задать переходные зоны, поведение АЧХ в которых не имеет значения. В этих зонах значение весовой функции должно быть нулевым.
В общем случае задача не имеет аналитического решения и поэтому должна решаться итерационными численными методами. Минимизация ошибки приводит к появлению больших выбросов АЧХ при попытке аппроксимировать ее скачкообразное изменение. Это связано с явлением Гиббса. Для уменьшения влияния эффекта Гиббса при этом может использоваться наложение ограничений на предельное абсолютное отклонение частотной характеристики от заданной.
Восстановление сигналов (решение обратной задачи)
Искажения
Одномерных сигналов
Восстановление сигналов
Интеграл свертки представляется выражением
(1)
где h(x) - функция, задающая искажение; f(x) - функция, которую необходимо восстановить.
Согласно теореме о свертке фурье-образ величины (1) равен
(2)
где F(u) - функция, связанная с функцией f(x) двумерным преобразованием Фурье; H(u) - фурье-образ оптической передаточной функции.
Идеализированная задача конечной деконволюции такова: заданы функции b(x) и h(x) , требуется восстановить функцию f(x) при условии, что все три величины имеют конечную протяженность.
Из соотношения (2) следует, что эту задачу можно решить следующим образом
(3)
Операция деления внутри фигурных скобок в выражении (3) называется простой инверсной фильтрацией. Термин "фильтрация" здесь употребляется по аналогии с классической теорией цепей и современной теорией обработки сигналов. Классический фильтр представляет собой устройство, которое изменяет спектр временных частот сигнала. Спектр B(u) есть функция пространственной частоты.
Оптическая передаточная функция H(u) изменяет спектр пространственных частот B(u) в результате применения указанной выше операции деления.
Поскольку обработанные изображения обычно хранятся в памяти ЭВМ в виде квантованных значений, в технике обработки изображений, как правило, используются цифровые, а не классические аналоговые фильтры. Цифровой фильтр определяется дискретным массивом, вообще говоря, комплексных чисел, который изменяет в процессе некоторой операции обработки спектр пространственных частот. Следовательно, обе функции, h(x) в формуле (1) и H(u) в формуле (2), могут рассматриваться как фильтры (и в большей части приложений они реализуются в цифровом виде). Общепринятая классификация цифровых фильтров возникла в теории обработки сигналов как функций времени, и этой классификацией можно пользоваться в теории обработки одномерных изображений, т. е. сигналов как функций (одной) пространственной переменной. Мы перенесем соответствующую терминологию на двумерный случай. Понятие "отсчета" в теории обработки сигналов переходит в понятие "элемента изображения" в теории обработки изображений. Как отсчеты, так и элементы изображений должны квантоваться по амплитуде до их цифровой обработки. Изображение, к которому должна быть применена операция фильтрации, называется заданным изображением, и о нем говорят как о состоящем из заданных элементов изображения. Элементы профильтрованного изображения называются выходными элементами изображения.
В случае нерекурсивного цифрового фильтра каждый выходной элемент изображения представляет собой взвешенную сумму заданных элементов изображения.
В случае же рекурсивного цифрового фильтра каждый выходной элемент изображения есть взвешенная сумма заданных элементов изображения и рассчитанных ранее выходных элементов изображения. Все практически реализуемые цифровые фильтры, конечно, описываются массивами конечных размеров (в одномерном случае конечный фильтр часто называют коротким). Цифровой фильтр называется прямым, если он применяется в плоскости изображения, и спектральным - если он применяется в частотной плоскости.
Каузальный фильтр является односторонним в том смысле, что его отклик всегда отстает от входного воздействия (это несколько искусственно в двумерном случае, но, конечно, имеет очень важное значение для операций одномерной фильтрации, которые лежат в основе обработки сигналов как функций времени).
Каузальные фильтры почти всегда реализуются как прямые.
Мультипликативный цифровой фильтр представляет собой спектральный фильтр, в котором каждый выходной отсчет получается как произведение заданного элемента входного сигнала на один элемент массива фильтра.
Решение задачи деконволюции заключается в обращении двумерной свертки. Термин "деконволюция" охватывает наиболее важные и широко используемые методы обработки изображений. Необходимость в такой операции возникает во всех областях науки, связанных с измерениями. По методах деконволюции существует большое число работ [1].
Задача деконволюции может быть решена несколькими способами. Выбор наиболее подходящего для решения этой задачи метода зависит от ряда факторов, в том числе от формы и протяженности функции распространения точки (ФРТ), характера исходного изображения и степени усечения его кадровым окном записывающего устройства.
Существуют различные подходы к задаче деконволюции. Эти подходы включают нерекурсивный и рекурсивный методы фильтрации в плоскости изображения, прямые матричные методы и методы максимальной энтропии и максимального правдоподобия.
Одним из наиболее важных практических методов деконволюции является метод слепой деконволюции.
Кроме известных традиционных приложений деконволюции существуют и различные ее экзотические применения. Одно из наиболее замечательных таких применений - восстановление методом слепой деконволюции записей голосов знаменитых певцов на старых граммофонных пластинках.
Алгоритм деконволюции в частотной области
Существуют два принципиально различающихся способа устранения искажений, вносимых реальным регистрирующим прибором в наблюдаемый сигнал. Первый состоит в том, что при помощи искусных технических решений совершенствуют конструкцию реального прибора, однако по мере улучшения характеристик неизбежно возрастают сложность и стоимость аппаратуры. К тому же иногда характеристики сигнала (например, близкая по частоте помеха) не позволяют улучшать передающие свойства прибора.
Другим способом устранения искажений является апостериорная обработка сигнала с целью уменьшения влияния реальных характеристик прибора (сведение их к "идеальному" виду). Вопрос о редукции к идеальному прибору, не искажающему полезный входной сигнал был поставлен еще Рэлеем в 1871 г. в связи с некоторыми задачами спектроскопии и состоял в следующем: можно ли после опыта так обработать функцию, наблюдаемую на выходе некоторого реального прибора, чтобы полностью восстановить сигнал, поступивший на его вход. В такой постановке задача относится к классу некорректно поставленных, и в общем случае не может быть решена, однако на практике при соблюдении некоторых требований (ограниченность спектра рассматриваемого сигнала по частоте, отсутствие в рассматриваемом диапазоне частот нулей в передаточной функции прибора и т.д.) она может быть решена с достаточной точностью и иметь практическое значение.
Различные методы подобного восстановления сигнала хорошо развиты в области обработки изображений (см., например, работу [3]), однако в других областях в настоящее время не получили широкого распространения из-за необходимости цифровой обработки сигнала и большого объема требуемых вычислений (в частности, нам неизвестны медицинские приборы, реализующие такую коррекцию). Тем не менее существующий уровень компьютерной техники позволяет реализовать рассматриваемый алгоритм за приемлемое время (так обработка 1024 отсчетов на IBM PC/AT 80386 без сопроцессора занимает около 5 секунд и может быть ускорена за счет ряда специальных приемов). К тому же, как показывает анализ литературы, большинство исследователей уделяют внимание коррекции только амплитудных, но не фазовых искажений сигналов. В дальнейшем будет показана важность коррекции именно фазовых характеристик сигнала.
Как правило, реальные приборы с достаточной степенью точности являются линейными, и сигнал f(t) на их выходе описывается интегральным уравнением:
(1)
где h(t) - импульсная переходная характеристика прибора, s(t) - сигнал, поступающий на вход прибора. Это уравнение является уравнением свертки, и может быть записано как
(2)
где F(w), H(w), S(w) - фурье-образы функций f(t), h(t) и s(t), т.е. соответственно спектр отклика, передаточная функция системы и спектр входного сигнала. Из уравнения (2) следует, что по крайней мере формально, можно записать
(3)
откуда обратным преобразованием Фурье находим:
(4)
Формула (4) справедлива, если f(t) L2(-,), h(t) L1(-,), F(w)/H(w) L2(-,), и сохраняет силу, если H(w) обращается в нуль на множестве нулевой меры.
На практике применение формулы (4) сопряжено с рядом сложностей:
1. В действительности H(w) отлична от нуля лишь в конечном интервале частот. Радиотехнические приборы разрабатываются таким образом, что H(w) 0 вне частотного диапазона сигнала, поэтому естественной становится коррекция в диапазоне частот, ограниченном частотными характеристиками сигнала и зануление всех частот, где спектральная плотность мощности шума превышает сигнал. Если нуль частотной характеристики попадает в полосу частот сигнала, то некоторые способы разрешения данной проблемы приведены, например, в работе [2].
2. Присутствие в сигнале аддитивной помехи. Выходной сигнал прибора f(t) известен всегда приближенно, и содержит в себе случайную помеху v(t):
f(t) = fт(t) + v(t),
тогда согласно выражению (3) спектр восстановленного сигнала:
S(w) = Sт(w) + V(w)/H(w),
где V(w) - спектр помехи. Спектральная плотность случайной ошибки восстановления (дисперсия решения задачи) равна [3]:
(5)
где Rv(w)= |V(w)|2 - спектральная плотность мощности помехи. Реальная помеха содержит компоненту белого шума, и ее спектральная мощность стремится к конечному пределу при w . Поэтому интеграл (5) может не сходиться либо быть недопустимо большим. В этом случае можно рекомендовать ограничение частотного диапазона коррекции с подавлением ненужных частот спектра.
3. Погрешности, связанные с квантованием уровня сигнала, округлением при машинном представлении действительных чисел, и т.д. Оценка ошибок восстановления, обусловленных данными погрешностями рассматривается в литературе (например, [3]) и должна в каждом случае оцениваться отдельно. В наших задачах сколько-нибудь заметного пpоявления этих факторов замечено не было.
4.Граничные эффекты. Наиболее неприятным фактом при коррекции искажений сигналов являются краевые эффекты. На практике сигнал известен не на всей временной оси, а в диапазоне (-Т, Т) (рис. 1,а). Поэтому для формулы фильтрации в пространственной области (1) возникает вопрос о доопределении сигнала за границами рассматриваемого интервала. В простейшем случае считают, что за границами (-Т, Т) сигнал равен своему математическому ожиданию (рис.1,б). Также используется различная экстраполяция (напр. считают, что сигнал вне (-Т, Т) равен своему значению на границах интервала).
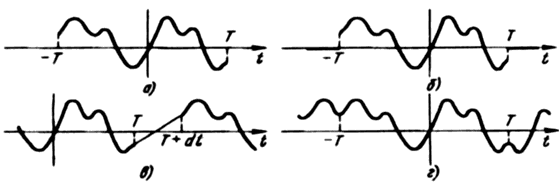
Рис 1. Варианты доопределения сигналов за границами выборки
При цифровой фильтрации (особенно при использовании аппарата преобразований Фурье), часто исходный сигнал считают периодически продолженным с периодом, равным длине исходной последовательности. Так как начало и окончание записи сигнала расположены в произвольные (независимые от сигнала) моменты времени, то длина исследуемого интервала не равна целому числу периодов сигнала, что приводит к несовпадению амплитудного значения (и значения производных амплитуды) сигнала в начальной и конечной точках и, как следствие, к появлению в спектре высокочастотных гармоник, а после фильтрации - к возникновению осцилляций на краях последовательности (эффект Гиббса). Некоторые исследователи рекомендуют в этом случае использование линейной аппроксимации между начальной и конечной точками (рис. 1,в, длина дополнения должна быть не менее удвоенной длительности импульсной характеристики фильтра) или четного продолжения исходной последовательности (рис. 1,г). Проведенные численные эксперименты показали, что хотя эти способы уменьшают высокочастотные выбросы спектра, однако сильно искажают его низкочастотную область. Более удачные результаты при использовании дискретного преобразования Фурье (ДПФ) получаются при использовании так называемых "весовых окон". Обычно они применяются при оценке спектра по малой выборке: предварительно сигнал умножают на быстро спадающую функцию, например, на кривую Гаусса:
(6)
где 2T - длительность выборки, | t | < T, а - параметр (наилучшие результаты получаются при 2.5 < а < 3), затем проводят Фурье-преобразование для оценки спектра. Другие весовые окна рассматриваются, например, в работе [4]. Их применимость в нашем случае определяют два фактора: скорость спада боковых лепестков и малые вычислительные погрешностями. Окно Ханна дает лучшие результаты в смысле отсутствия боковых лепестков, но на границах его значения близки к нулю, поэтому после фильтрации часть информации на концах интервала будет потеряна.
Исходный сигнал можно рассматривать как бесконечный, умноженный на прямоугольное весовое окно, что в частотной области эквивалентно свертке с Фурье-образом этого окна, функцией sinc(x) = sin(x)/x. В результате истинный спектр как бы "размывается" по частоте (боковые лепестки имеют уровень -13.3 дБ), что приводит
к неограниченности полученного спектра (даже если в качестве исходного сигнала взят sin(t));
к тому, что гармоника вносит ненулевой вклад во весь спектр сигнала (т.е. их невозможно разделить при фильтрации).
Предварительное умножение на функцию Гаусса приводит к тому, что свертка производится с ее Фурье-образом, а не с sinc(x), таким образом, за счет некоторого уширения самой спектральной полосы, сильно подавляются ее боковые лепестки (до уровня -45..-55 дБ в зависимости от параметра а), и спектр более точно аппроксимирует спектр реального бесконечного сигнала. На рис.2,а - представлен вычисленный спектр синусоидального сигнала с использованием прямоугольного окна (сплошная линия) и окна Гаусса (теоретически, спектр должен был бы иметь вид дельта-функции). После фильтрации, разумеется, надо вернуть сигнал к первоначальному виду, т.е. разделить на функцию Гаусса. Здесь может возникнуть единственная тонкость, связанная с округлением чисел при машинной обработке.
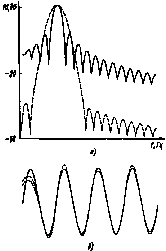
Рис. 2 Спектр мощности выборки синусоидального сигнала (сплошная линия) и спектр того же сигнала с использованием окна Гаусса (пунктирная линия) (а); видно расширение спектральной полосы и подавление боковых лепестков; исходная выборка (сплошная линия), она же после фильтрации (пунктирная), она же после фильтрации с применением окна Гаусса (штрих-пунктирная) (б)
Использование прямоугольного окна при фильтрации вносит заметные искажения на протяжении примерно трех периодов сигнала с каждой стороны, в то время как окно Гаусса позволяет уменьшить влияние краев выборки до 0.5 периода На рис.2,б представлен синусоидальный сигнал (сплошная линия), он же после проведения узкополосной фильтрации с применением окна Гаусса (штрих-пунктирная линия) и без применения окна Гаусса (штриховая линия). Вторым моментом, связанным с граничными эффектами, является то, что импульсная передаточная характеристика корректирующего фильтра должна быть конечной во времени, и ее длина должна быть много меньше 2Т. На практике это означает невозможность реализации прямоугольной АЧХ фильтра. Поскольку именно такую характеристику считают "идеальной", можно рекомендовать следующий алгоритм построения фильтра. В частотной области определяются амплитудно-фазочастотные характеристики требуемого фильтра, затем при помощи обратного фурье-преобразования вычисляется его импульсная характеристика, которая обрезается до нужной длины (чем короче - тем меньше влияние границ выборки, но и тем ниже порядок получающегося фильтра), и, для повышения гладкости АФЧХ, умножается на функцию Гаусса (6). После этого, вычисляя прямое фурье-преобразование, получим сглаженные АЧХ и ФЧХ нашего фильтра. В работе [5] приведен интересный способ фильтрации, когда помимо восстановления сигнала производится усиление его гармоник пропорционально соотношению сигнал/шум для каждой частоты:
где H(w) и H(w)* - передаточная функция прибора, и ее комплексно сопряженная величина, Rs(w) и Rv(w) - спектральные плотности мощности входного сигнала и шума соответственно.
Этот способ предполагает знание спектральных характеристик шума, и, вообще говоря, искажает спектр входного сигнала.
Вычислительные алгоритмы. Поскольку при обработке сигналов приходится искать компромисс между точностью и скоростью работы математических алгоритмов, то и мы в своем изложении будем уделять основное внимание именно этим двум факторам.
Коррекция исходного сигнала есть не что иное как фильтрация с передаточной функцией 1/H(w). Синтез подобного фильтра аналоговыми методами в общем случае невозможен, то единственным общим способом его реализации является апостериорная цифровая обработка.
Цифровой сигнал представляет собой значения реального аналогового сигнала, взятые через равные промежутки времени. Необходимую частоту дискретизации (время между отсчетами) определяют из теоремы Котельникова (она должна быть больше 2Fмакс, где Fмакс - максимальная присутствующая в спектре сигнала частота). На практике используют частоту, превышающую частоту Котельникова (Найквиста) в 2-5 раз. Фильтрация в цифровой области имеет свои особенности, преимущества и недостатки, и сходна с аналоговой фильтрацией. Простейшим и часто используемым методом цифровой фильтрации является прямое вычисление свертки входного сигнала с импульсной передаточной характеристикой (ИПХ) фильтра по формуле (для нерекурсивного фильтра):
которая представляет собой дискретный аналог формулы (1), здесь Nипх - количество отсчетов импульсной передаточной характеристики. Для вычислений по этой формуле требуется произвести Nc Nипх умножений и столько же сложений (Nc - число отсчетов сигнала), что при длинной ИПХ занимает больше времени, чем реализация такого же фильтра в частотной области.
Согласно формуле (2) свертка сигналов во временной области аналогична перемножению их спектров. Аналогом преобразования Фурье для дискретных сигналов является дискретное преобразование Фурье (ДПФ):
(7)
Его главное отличие от непрерывного преобразования Фурье - цикличность, т.е. и сигнал, и его спектр являются периодическими с периодом N. Наиболее употребительные свойства ДПФ:
A*N-S -- ДПФ комплексно-сопряженного сигнала а;
AS = A*N-S -- ДПФ действительного сигнала;
AS = AN-S -- ДПФ четно-симметричного сигнала;
AS = -AN-S -- ДПФ нечетно-симметричного сигала;
При непосредственных вычислениях по формуле (7) требуется произвести N2 умножений и сложений комплексных чисел, поэтому на практике пользуются быстрым преобразованием Фурье (БПФ), в котором за счет некоторого дополнительного расхода машинной памяти и использования рекурсии число операций уменьшено до N logN, что при больших выборках дает существенный выигрыш во времени. Существуют различные алгоритмы БПФ, рассматриваемые в специальной литературе (например, [3]), суть которых в том, что исходная последовательность делится на несколько меньших частей, для каждой из которых вычисляется ДПФ (время вычисления которого меньше, т.к. N12+N22 < (N1+N2)2), а затем по найденным спектрам вычисляется спектр исходной последовательности.
Кроме алгоритма БПФ, двукратного выигрыша по времени выполнения можно достичь, применяя совмещенные алгоритмы ДПФ. Для последовательностей вещественных чисел коэффициенты Фурье с номерами k и N-k являются комплексно-сопряженными числами (свойство 2). Поэтому можно либо преобразовывать две последовательности одновременно, либо разбить исходную последовательность на две, одновременно преобразовать их, а потом пересчитать результаты на всю последовательность в целом. Используя первый способ, из последовательностей Ak и Bk создают последовательность Ck, такую, что: Ck = Ak + i Bk и вычисляют ее ДПФ (Fr). ДПФ исходных последовательностей находят по соотношениям:
учитывая, что AN-r = Ar, BN-r = Br.
При втором способе последовательность A длины 2N разбивается на две подпоследовательности: четных элементов (Аr_even) и нечетных (Аr_odd). Далее вычисления ведутся как и в первом способе, а затем по формуле
находят ДПФ исходной последовательности. Если в исходной последовательности или в ее ДПФ заведомо много нулей (например, некоторые гармоники в процессе фильтрации должны быть обнулены), то дополнительной экономии времени можно достичь просто их не вычисляя.
Поскольку обычно реальные сигналы вводятся в ЭВМ через АЦП, т.е. являются целыми числами, то естественно для них вести обработку в целочисленной области (которая в 3-10 раз по скорости превышает обработку действительных чисел). Однако в этом случае встает вопрос о точности проводимых преобразований, что ограничивает применимость этих методов для коррекции сигналов. Здесь не приведены численные эксперименты, а показанные ниже методы указаны для полноты обзора, поскольку в литературе встречаются редко.
Наиболее просто использование целых чисел реализуется в методе прямой свертки. Найденные коэффициенты просто домножаются на некоторое число (чтобы получить необходимую точность), а в процессе свертки полученное отфильтрованное значение делится на то же число.
В работах [3, 6] приводится метод квантованного БПФ. Суть его в том, что значения синуса и косинуса квантуются, т.е. принимают дискретные значения, например -1, 0, 1 при трех уровнях и -1, -1/2, 0, 1/2, 1 при пяти уровнях (вообще говоря, это разложение сигнала по другим базисным функциям). В этом случае умножения либо вообще отсутствуют, либо заменяются сдвигами. Для фильтрации изображений этот метод дает вполне приемлемые результаты.
Существует еще ряд базисов (функции Уолша, Хаара, и т.д.), разложение по которым привлекает внимание тем, что операции можно вести с целыми числами, однако мы не исследовали их применимость для цифровой коррекции сигналов.
Обобщение. После проведенных исследований мы остановились на следующей схеме вычислений.
Предварительно измеряем или вычисляем передаточную функцию прибора H(w). Вычисляем передаточная функция восстанавливающего фильтра 1/H(w) (если предполагается прямая свертка во временной области, то затем вычисляем импульсную характеристику (обратное ДПФ от передаточной характеристики), с учетом приведенных выше замечаний.
Исходный сигнал умножаем на функцию окна.
Проводим фильтрацию-восстановление (во временной или в частотной области).
Отфильтрованный сигнал делим на функцию окна.
Вопрос о том, в какой области проводить фильтрацию-восстановление - во временной или в частотной, решается исходя из требуемой точности и скорости обработки. В частотной области можно достичь наивысшей точности при восстановлении и наиболее крутых фронтов фильтров при приемлемом времени вычислений (как уже упоминалось - примерно 5 с на IBM PC/AT для двух последовательностей в 1024 отсчета при одновременной обработке), однако неудобство состоит в необходимости сначала ввести всю последовательность, а затем ее обработать, к тому же при использовании БПФ ограничения накладываются на число точек в последовательности и появляются довольно жесткие требования к объему машинной памяти. Во временной области три последних недостатка отсутствуют, но сильно возрастает время вычислений, которое можно сократить за счет выбора короткой ИПХ (ориентировочно меньше 0.1N, где N - длина исходной последовательности) и проведения операций с целыми числами, однако при этом сильно проигрываем в точности.
Эффекты квантования в цифровых фильтрах
Неизбежное округление разнообразных коэффициентов, используемых в алгоритмах цифровой обработки сигналов, приводит к тому, что параметры фильтров и других устройств отличаются от желаемых, причем возможны ситуации, когда эти отличия весьма существенны. Кроме того, из-за округления промежуточных результатов может происходить накопление вычислительных погрешностей, также искажающих конечный результат. Эти эффекты будут рассмотрены в данном разделе.