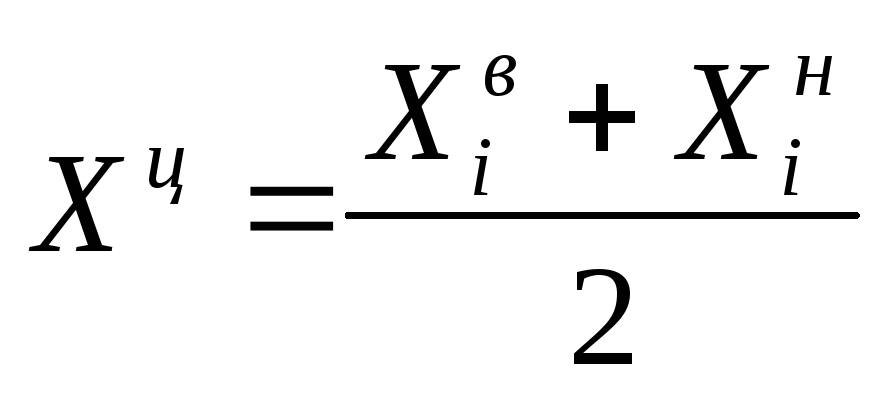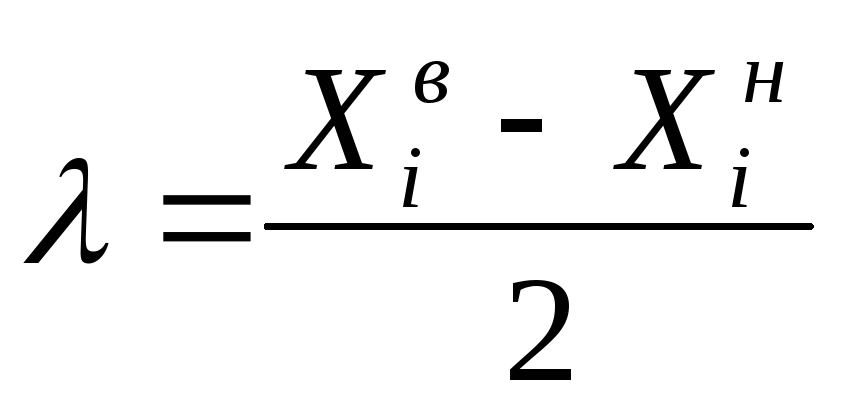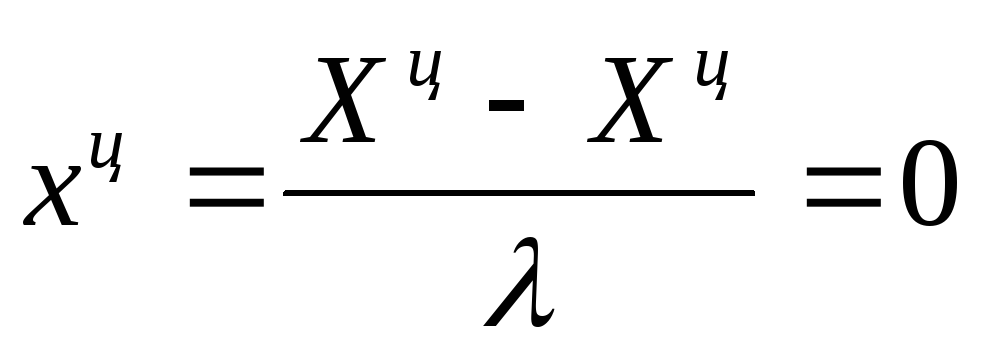5.4 Планы первого порядка

Процессы химической технологии являются сложными. Выражается это в том, что на процесс влияет не один, а ряд факторов. Эксперимент в этом случае называется многофакторным. Планирование эксперимента с целью оптимизации начинают тогда, когда процесс предварительно исследовался. Информация, содержащаяся в предыдущих исследованиях, называется априорной. Выбор экспериментальной области факторного пространства связан с тщательным анализом априорной информации.

Планы первого порядка служат для построения математической модели в виде полиномов первой степени (линейных уравнений регрессии).

(5.1)

5.4.1.Полный факторный эксперимент

Полный факторный эксперимент – это эксперимент, в котором реализуются все возможные сочетания уровней факторов.

Необходимое количество опытов (n) при этом определяется по формуле:

(5.2)

где N – количество уровней факторов,

k– количество факторов.

Порядок построения плана:

а) на основании априорной информации выбираем наилучшие условия проведения эксперимента и принимаем эту точку за центр плана. Значения факторов в этой точке называют основным, нулевым или центральным уровнем (Х_i^ц);

б ) выбираем интервал варьирования для каждого фактора () и вычисляем верхний (

100 200 300

Х_i^в ) и нижний (Х_i^н) уровни факторов.

Х^в = 300, Х^н = 100,  = 100.

Интервал варьирования – это число (свое для каждого фактора) прибавление которого к основному дает верхний уровень, а вычитание из основного – нижний. Или иными словами – это расстояние на координатной оси между центральным и верхним (нижним) уровнем фактора.

(5.3)

Известно, что оптимальными свойствами обладают планы первого порядка, в которых каждый фактор принимает лишь два значения, варьируется на двух уровнях, верхнем и нижнем.

Мы будем изучать только такие планы.

в) кодируем переменные по формулам:

(5.4)

где х^в, х^н – верхний и нижний уровни факторов в кодированном виде;

Х^в, Х^н – верхний и нижний уровни факторов в натуральном виде.

Кодирование переменных проводят для упрощения вычислений и интерпретации полученных результатов. Координаты центра плана равны 0.

(5.5)

г) строим матрицу планирования.

Рассмотрим построение матрицы планирования на примере двухфакторного эксперимента.

K=2 n=2²=4

Допустим Х₁ – температура, Х₂ – давление.

Х₁ – принимает значения: Х₁^в=300⁰С, Х₁^н=100⁰С, Х₁^ц=200⁰С.

Х₂ – принимает значения: Х₂^в=3атм, Х₂^н=1атм, Х₂^ц=2атм.

Область факторного пространство для данного эксперимента будет иметь вид (рис. 1) квадрата с вершинами 1,2,3,4.

Перенесем начало координат в точку 5, то есть в центр области факторного пространства. Это действие соответствует переходу к новой безразмерной системе координат с началом в центре исследуемой области.

Рисунок 5.1 – Область факторного пространства

Координаты точек в новой системе записывают в виде таблицы, называемой матрицей планирования эксперимента (а). Этой матрице соответствует матрица в натуральном виде (б).

Таблица 5.1 Матрицы планирования эксперимента

n	x1	x2		n	X1	X2
1	-1	-1		1	100	1
2	+1	-1	(а)	2	300	1	(б)
3	-1	+1		3	100	3
4	+1	+1		4	300	3

Каждая строка полученной матрицы – это условия проведения одного опыта, в результате которого получают значение параметра (У).

Правило построения матрицы:

-первый столбец матрицы – фиктивная переменная х₀ всегда равна (+1);

-второй столбец – равномерное чередование знака (+) и (-) в столбце(+1,-1, +1,-1) и т.д.;

-третий столбец – чередование двух строк одного знака, двух другого;

-к-ый столбец – чередование 2^(к-1) одноименных знаков.

Например, в 5-ом столбце 2⁴=16 знаков +1 и 16 – минус 1 .

Свойства матрицы ПФЭ типа 2^k:

Мы научились строить матрицы ПФЭ с факторами на 2 уровнях (в кодированном виде). Теперь выясним какими свойствами эти матрицы обладают независимо от количества факторов.

Первые два свойства следуют непосредственно из построения матрицы.

1 свойство – симметричность относительно центра эксперимента. Формулируется следующим образом: алгебраическая сумма элементов вектор-столбца каждого фактора равна 0 , или

(5.6)

2 свойство – так называемые условия нормировки – сумма квадратов элементов каждого столбца равна количеству опытов, или

(5.7)

Эти два свойства позволяют значительно упростить вычисление коэффициентов в_i и дисперсий s_вi .

3 свойство – ортогональность матрицы планирования - сумма почленных произведений любых двух вектор-столбцов матрицы равна 0.

(5.8)

где j не равен u j,u = 0,1,2…k.

Это свойство позволяет вычислять коэффициенты уравнения регрессии независимо друг от друга, поэтому после исключения незначимых коэффициентов из уравнения не требуется перерасчет оставшихся коэффициентов b_i.

4 свойство – ротатабельность - точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.

д) проводим эксперимент по матрице.

Каждая строка матрицы – это условие проведения одного опыта. В результате эксперимента получаем значение параметра оптимизации (У). Причем, все опыты дублируются для того чтобы можно было рассчитать дисперсию воспроизводимости. Установлено, что наилучших результатов достигают, если проводят не менее 3 параллельных опытов. Порядок опытов в матрице не должен определять реальную последовательность проведения опытов. Опыты должны быть рандомизированы во времени, то есть выполняться в случайном порядке. Особенно это касается параллельных опытов.

е) проводим регрессионный анализ результатов(статистическую обработку результатов).

О бычно, реализуя активный эксперимент проводят одинаковое количество параллельных опытов. Поэтому и применяют первую схему регрессионного анализа ,согласно которой вычисляют:

а) построчные математические ожидания (y_i):

(5.9)

где m – количество параллельных опытов;

y_i – результаты эксперимента;

в) построчные дисперсии (S_i²):

(5.10)

г) проверяют однородность построчных дисперсий по критерию Кохрена:

(5.11)

если G_p <G_табл. – дисперсии однородны,

где G_р – расчетный критерий Кохрена,

G_табл – табличный критерий Кохрена,

S²_max – максимальная построчная дисперсия,

n – количество опытов;

д) дисперсию воспроизводимости (S²_воспр):

(5.12)

е) методом наименьших квадратов вычисляем коэффициенты уравнения регрессии (в_i ). В связи с тем, что матрица планирования симметрична и нормирована формулы для вычисления в_i значительно упрощаются и

выглядят следующим образом:

(5.13)

где x_ij – значения факторов в кодированном виде;

(5.14)

ж) проверяем значимость коэффициентов в_i по критерию Стьюдента:

(5.15)

где t_p –расчетный критерий Стъюдента;

S_bi – дисперсия коэффициентов b_i ;

t_табл.- табличный критерий Стъюдента.

(5.16)

если t_р>t_табл. – коэффициент в_i значим, в противном случае – не значим. Исключаем незначимые факторы из уравнения регрессии.

Значимость коэффициента bi свидетельствует о том, что фактор, соответствующий этому коэффициенту, оказывет существенное влияние на процесс .В противном случае, фактор в пределах области факторного пространства не оказывает существенного влияния на процесс и поэтому из дальнейших расчетов исключается.

з) проверяем адекватность уравнения регрессии по критерию Фишера (F):

(5.17)

где Fр – расчетный критерий Фишера;

S_ад² – дисперсия адекватности;

S_воспр² – дисперсия воспризводимости.

(5.18)

где у_i^р - расчетный параметр оптимизации;

l – количество значимых коэффициентов в уравнении регрессии, считая b₀.

Находим табличный критерий Фишера, который зависит от степеней свободы числителя и знаменателя.

Значения степеней свободы для числителя (f_ч) и знаменателя(f_зн) вычисляют по формулам:

f_ч = n – l; f_зн = (m – 1). (5.19)

Если F_р<F_табл. – уравнение адекватно. В противном случае –неадекватно и следует перейти к планам более высокого порядка.