Нормальный алгоритм

Один из способов уточнения содержательного по­нятия алгоритма, рассматриваемых в теории алгоритмов (см. Теория алгоритмов). Схема нор­мального алгоритма была предложена советским логиком Л. А. Марковым. Поэтому нормальные алгоритмы называют также алгоритмами Маркова или нормальными алгоритмами Маркова.

Нормальные алгоритмы оперируют со словами конечной длины, преобразуя их друг в друга с по­мощью подстановок, т. е. замены одних частей сло­ва на другие. Этот процесс очень напоминает процедуру выполнения заданий типа: "Путем за­мены букв в слове по одной превратить слово "слон" в слово "муха". Если бы процесс такого преобразо­вания описывался алгоритмом Маркова, то было бы сказано, что он работает над алфавитом русского языка, а используемые им подстановки имеют вид:

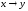, где х и у - какие-то буквы русского алфа­вита.

Для нормального алгоритма надо задать алфа­вит, над которым он работает, конечное множество допустимых подстановок, а также порядок их при­менения. Множество подстановок нужного нам ал­горитма могло бы выглядеть, например, так:

Порядок применения подстановок задается с помощью следующего правила, одинакового для всех нормальных алгоритмов. Для исходного слова взять первую подстановку. Если ее левая часть имеется в исходном слове, то произвести замену ее первого вхождения в слово на правую часть подстановки. Если первая подстановка к исходному слову применена быть не может, то проверяется следующая по порядку подстановка. Если никакая из подстановок к исходному слову неприменима, то процесс преобразования завершен. Если некоторая подстановка оказалась использованной, то необходимо проверить, нет ли в правой части специального знака "!". Если его нет, то слово, получившееся после преобразования, снова считается исходным и весь процесс начинается заново. Если же знак "!" есть, то процесс преобразования прекращается.

Применим теперь нормальный алгоритм с приведенными подстановками для исходного слова "слон". Первая подстановка к нему неприменима, так как в исходном слове нет буквы "я". Вторая подстановка применима, и слово "слон" превращается в результате ее использования в слово "суон". По­скольку в правой части второй подстановки нет знака "!", то слово "суон" становится исходным и к нему снова надо применять первую подстановку. Но ни она, ни вторая подстановка теперь не могут быть использованы, а третья подстановка превращает "суон" в новое исходное слово - "муон". Далее про­цесс протекает аналогично, и вскоре в качестве ис­ходного слова возникает слово "муха". К нему оказывается неприменимой ни одна из подстановок алгоритма, и действие алгоритма завершается.

Если бы исходное слово было другим, то алго­ритм работал бы иначе. Например, слово "ветер" преобразуется им в слово "берет", а шестая подста­новка из-за наличия знака "!" не дает продлиться процессу дальше и превратить "берет" в "бетет" и преобразовывать его далее.

В общей схеме нормального алгоритма нет нужды ограничиваться лишь отдельными буквами. Подстановки имеют вид: 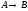, где слева и справа стоят конечные слова произвольной длины в том ал­фавите, над которым работает алгоритм.

В теории алгоритмов строго доказано, что по своим возможностям преобразования нормальные алгоритмы эквивалентны машинам Тьюринга и другим формальным моделям, уточняющим интуи­тивное понятие алгоритма.