
- •032900 – Русский язык и литература;
- •032600 – История;
- •033200 – Иностранный язык;
- •Пояснительная записка
- •032900 – Русский язык и литература;
- •032600 – История;
- •033200 – Иностранный язык;
- •Программа курса
- •Математические и логические основы информатики.
- •II. Арифметические и логические основы персонального компьютера.
- •III. Теория алгоритмов и формальных грамматик.
- •IV. Программные средства персонального компьютера.
- •Учебный план
- •I лекции (20 часов)
- •Методические указания к лекциям
- •Лекция 1
- •Лексические функции как пример математизации объектов лингвистики
- •Функция как математическое понятие
- •Функция в лексике
- •Отличие лексической функции от числовой
- •Обозначение
- •«Склеенные» функции
- •Типы лексических функций
- •Возможности использования лексических функций
- •Лекция 2-3 Алгебра высказываний. Логические функции. Законы булевой алгебры
- •Лекция 4 Перевод чисел из одной позиционной системы счисления в другую. Арифметика в различных системах счисления.
- •Лекция 5 Количество информации
- •Лекция 6 Архитектура эвм
- •4. Алгоритм решения любой задачи представляется в виде последовательности слов, называемых командами, которые определяют наименование операции и слова информации, участвующие в операции.
- •Устройство процессора
- •Лекция 7 Алгоритм
- •Нормальный алгоритм
- •Лекция 9 Понятие операционных систем
- •Приложение к лекции 1 Синтаксический граф
- •Синтаксическое дерево
- •Типы синтаксических деревьев
- •Дерево подчинения
- •Стилистическая диагностика Индивидуальный синтаксис писателя
- •Перевод особенностей авторского стиля на формальный язык синтаксических деревьев
- •Пушкинская, лермонтовская и гоголевская фразы — сходства и различия
- •Компьютерный практикум.
- •Частотный анализ в филологических исследованиях (на базе словарей)
- •Работа с программой PhotoShop 6
- •Создание шаблона титульного листа диплома в программе word. Лабораторная работа № 1. Изучение макрокоманд программы Word
- •Общие навыки Включение компьютера
- •Нажатие левой клавиши устройства «Мышь».
- •Установка текстового курсора в нужную позицию
- •Работа с оконным интерфейсом операционной системы Windows
- •Переход на вкладку в окне.
- •Работа с файловой системой операционной системы Windows 2000 Открытие окна Microsoft Word.
- •Закрытие окна программы Microsoft Word
- •Сохранение документа (файла) на диске.
- •Создание новой папки.
- •Открытие папки.
- •Поиск нужной папки
- •Открытие документа.
- •Создание нового документа
- •Копирование выделенного объекта.
- •Вырезание выделенного объекта.
- •Вставка скопированного (вырезанного) объекта.
- •Работа с файловой системой операционной системы Windows 2003 Открытие окна программы Microsoft Word
- •Закрытие окна программы Microsoft Word
- •Создание новой папки.
- •Открытие папки.
- •Поиск нужной папки
- •Открытие документа.
- •Сохранение документа (файла) на диске.
- •Создание нового документа
- •Копирование выделенного объекта в буфер обмена.
- •Вставка скопированного (вырезанного) объекта из буфера обмена.
- •Работа в программе Word Форматирование текста Установка автоматического переноса слов.
- •Установка параметров страницы.
- •Нумерация страниц.
- •Установка левой границы текста с помощью бегунка
- •Установка параметров абзаца.
- •Установка режима выравнивания.
- •Установка размера шрифта (кегля).
- •Выбор гарнитуры шрифта
- •Установка типа шрифта
- •Переход в режим набора текста курсивом (полужирным, с подчеркиванием).
- •Отмена набора текста курсивом (полужирным, с подчеркиванием).
- •Выделение текста (строки, слова, символа).
- •Гашение выделения текста (строки, слова, символа).
- •Изменение регистра букв текста
- •Изменение настройки автотекста: «Делать первые буквы предложений прописными.»
- •Маркировка и нумерация списка
- •Установка уровня вложенности заголовка.
- •Создание оглавления
- •Вставка объектов Вставка рисунка из библиотеки рисунков.
- •Перемещение объекта
- •Выделение объекта иди группы объектов
- •Вырезание выделенного объекта.
- •Изменение размера картинки
- •Вставка надписи.
- •Выделение надписи.
- •Заведение текста в надпись
- •Изменение размера надписи
- •Создание эффекта тени сзади надписи.
- •Установка режимов обтекания текстом картинок.
- •Установка режимов обтекания текстом объектов.
- •Вставка подписи к рисункам
- •Группировка объектов
- •Рисование стрелок и отрезков прямых линий.
- •Удаление объекта
- •Изменение направления текста в надписи.
- •Закрашивание фона надписи
- •Работа с таблицами Вставка таблицы
- •Выделение ячеек таблицы.
- •Вызов редактора формул.
- •Статистика Установка параметра проверки статистика удобочитаемости.
- •Подсчет количества вхождений заданного фрагмента текста в документ.
- •Выполнить сканирование и распознавание документов в программе Fine Reader 7.
- •Лабораторная работа №2 Создание текстового документа в редакторе Microsoft Word.
- •Лабораторная работа № 3 Набор филологических текстов.
- •Лабораторная работа №4 Создание таблиц.
- •Лабораторная работа № 5 Вставка объектов (рисунков и надписей) в текст.
- •Система высшего и центрального управления в Российской империи в первой половине XIX в.
- •Лабораторная работа 6. Набор математических объектов и формул.
- •Лабораторная работа № 7 Анализ удобочитаемости текста. Выбор тематической и удобочитаемой литературы с помощью команд программы Microsoft Word.
- •§ 1. Сущность методов осуществления целостного педагогического процесса и их классификация
- •Задание 3 .Выбор удобочитаемого тематического текста из сети Интернет с помощью команд программы Microsoft Word.
- •Лабораторная работа № 8 Расчет простых и сложных процентов
- •Основные определения.
- •Задача №1:
- •Задания для самостоятельной работы:
- •Лабораторная работа № 9 Расчеты итоговых сумм выплат при покупках в кредит
- •Основные определения.
- •Лабораторная работа № 10 Частотный анализ поэтических текстов по начальной букве
- •Лабораторная работа №11 Частотный анализ поэтических текстов по всем буквам.
- •Лабораторная работа № 12 Частотный анализ при обработке исторических фактов и географических названий.
- •Строка заголовков столбцов
- •Лабораторная работа № 13 Частотный анализ в филологических исследованиях (на базе словарей)
- •Лабораторная работа № 14 Создание иллюстративных материалов к уроку с помощью программы Power Point –2000 с использованием Internet ресурсов.
- •Лабораторная работа №15 Работа с программой PhotoShop 6
- •Лабораторная работа № 16 Обработка материалов тестовых опросов в программе excel
- •Лабораторная работа № 17 Создание шаблона титульного листа диплома в программе word.
Лекция 7 Алгоритм
Содержание понятия "алгоритм" можно определить следующим образом. Алгоритм — предписание, однозначно задающее процесс преобразования исходной информации в виде последовательности элементарных дискретных шагов, приводящих за конечное число их применений к результату.
Алгоритмы возникли вместе с появлением математики. Школьный курс математики предлагает большой выбор алгоритмов: алгоритмы сложения и умножения "столбиком", деления "углом", приведения дробей к общему знаменателю, построения биссектрисы угла и т. д. В высшей математике алгоритмов еще больше, причем наряду с численными алгоритмами (решение дифференциальных уравнений, задач математического программирования и др.) появляются алгоритмы над нечисловыми объектами (логическими выражениями, последовательностями произвольных символов, графами и т. п.).
Алгоритм — это точная инструкция, а инструкции встречаются практически во всех областях человеческой деятельности. Возможны алгоритмы проведения физического эксперимента, сборки шкафа или телевизора, обработки детали. Однако не всякая инструкция есть алгоритм. Инструкция становится алгоритмом только тогда, когда она удовлетворяет определенным требованиям. Эти требования частично сформулированы в начале статьи, хотя упомянутые в определении понятия однозначности и элементарности сами нуждаются в уточнении. Алгоритм однозначен, если при применении к одним и тем же данным он дает один и тот же результат. Но как по описанию алгоритма определить, однозначен он или нет? В каком случае шаги считаются элементарными?
Может возникнуть встречный вопрос: а так ли уж необходимо иметь точное определение алгоритма? В конце концов, в течение более двух тысячелетий люди создавали различные алгоритмы, не задумываясь над тем, что такое алгоритм вообще. Ответ на этот вопрос связан с двумя аспектами: теоретическим и практическим. С точки зрения самой математики желательно иметь дело только с точно определенными понятиями. Это нужно, например, для того, чтобы утверждать о некотором процессе, что он является алгоритмом или не является таковым. Точное определение важно и тогда, когда возникает желание доказать что-либо, относящееся к свойствам алгоритмов или к их возможностям. Этот аспект проблемы отражен в статье "Теория алгоритмов".
Здесь же речь пойдет о практическом аспекте, связанном с понятием алгоритма и с широким использованием этого понятия в программировании и вычислительной технике. Ведь всякий алгоритм есть некоторая программа действия, а машинные программы с этой точки зрения и есть точные инструкции на выполнение некоторых процедур. Это наводит на мысль, что программы — это записи некоторых алгоритмов, а программирование есть процесс перевода записей алгоритмов на язык, понятный машине.
От программ мы ожидаем практической результативности. Вряд ли могут представлять интерес программы, которые никогда не приводят к результату. Поэтому и в практическом аспекте важно уточнить понятие алгоритма.
Возвратимся к тому словесному определению, которое было приведено в начале статьи. Если используемые там на интуитивном уровне понятия однозначности, элементарности и результативности попытаться определить через какие-то другие понятия, то они, в свою очередь, также потребуют уточнения. Получается замкнутый круг. Чтобы вырваться из него, можно использовать следующий путь. Исходно задается лишь общая схема определения алгоритма. А ее детализация производится с помощью конкретного набора средств, которыми разрешается пользоваться в рамках данной алгоритмической модели. Эти модели могут быть теоретическими (см. Теория алгоритмов) и практическими. Последний тип моделей связан с реализацией алгоритмов на ЭВМ.
Схема определения алгоритма в практической модели выглядит следующим образом.
1. Всякий алгоритм применяется к исходным (входным) данным и выдает результаты (выходные данные). Кроме того, в ходе работы алгоритма появляются различные промежуточные данные. Поэтому должны быть указаны виды данных, с которыми могут работать алгоритмы. Для описания данных, во-первых, фиксируется набор элементарных символов (алфавит данных) и, во-вторых, даются правила построения сложных данных из простых. Примеры простых данных: целые и действительные числа, логические переменные, символьные переменные. Примеры сложных данных: массивы чисел, изображения на экране ЭВМ.
2. Данные для своего размещения требуют памяти. В ЭВМ память состоит из одинаковых ячеек, каждая из которых может содержать один или несколько символов алфавита данных. Таким образом, единицы объема данных и памяти согласованы, и в прикладных алгоритмических моделях объем данных можно измерять числом ячеек, в которых данные размещены.
3. Элементарные шаги алгоритма состоят из базовых действий, число которых конечно. В прикладных алгоритмических моделях под действиями можно подразумевать машинные команды, входящие в состав системы команд ЭВМ. При записи алгоритмов на языках программирования более высокого уровня, чем машинный язык, в качестве базовых действий могут выступать операторы, входящие в состав синтаксиса данного языка программирования.
4. Последовательность шагов алгоритма должна быть однозначной. Не допускается произвола при выборе очередного шага алгоритма. Обязательно должны быть зафиксированы начальный и заключительный шаги алгоритма.
Все шаги, которые встречаются в алгоритме, можно разделить на условные и безусловные. После безусловного действия либо выполняется действие, расположенное вслед за ним в описании, либо однозначно указывается, какой шаг надо выполнять. Условное действие связано с проверкой условия и указывает два действия, которые могут последовать за ним: одно выполняется, если условие соблюдено;
другое — если не соблюдено. Примером такого действия является команда условного перехода.
5. Точность записи алгоритма связана с использованием жесткого синтаксиса. Любая синтаксическая вольность (скажем, замена запятой на точку с запятой), любая ошибка в синтаксисе будут обнаружены и потребуют исправления.
6. Всякая алгоритмическая модель предполагает некоторый механизм исполнения алгоритмов, который обеспечивает доступ к ячейкам памяти, а также имеет средства для выполнения всех элементарных действий и управления процессом вычисления (т. е. пуском, остановкой и соблюдением нужной последовательности действий). Физическая реализация этого механизма (электронная, механическая или какая-либо другая) с алгоритмической точки зрения несущественна, хотя, разумеется, от нее зависят такие важные показатели, как скорость реализации алгоритма, надежность и т. д. Речь идет лишь о функциональной схеме механизма. В машинных моделях он описан непосредственно (машина и есть такой механизм). Для языковой модели путь от описания к реализации лежит через транслятор — специальную программу, которая перерабатывает текст на алгоритмическом языке в последовательность машинных команд. В роли исполнителя алгоритма может выступать и человек.
Как видим, для того чтобы набор инструкций можно было назвать алгоритмом, он должен удовлетворять многим достаточно жестким требованиям. Поэтому при описаниях алгоритмов, предназначенных для передачи другому человеку (например, в научных публикациях или при постановках задач), эти требования в полном объеме, как правило, не соблюдаются. Последствия такого несоблюдения могут быть различными. В одних случаях их выполнение связано лишь с некоторой рутинной работой, требующей профессиональных навыков и времени. Такие описания воспринимаются однозначно и в уточнениях нуждаются только тогда, когда дело доходит до программирования. В других случаях процесс уточнения может привести к полной переделке исходного текста. Короче говоря, путь от полуалгоритмического описания, имеющего лишь некоторые черты алгоритма, до настоящего алгоритма (который, как правило, имеет вид программы) может быть трудным. Пройти его — задача программиста. Однако, если в исходном описании есть неоднозначности, программисту может потребоваться помощь автора предлагаемой процедуры. Чтобы пояснить, о чем идет речь, рассмотрим простой пример.
Дано: последовательность чисел.
Требуется: найти в этой последовательности максимальное число.
Метод решения:
1. В некоторой памяти М запоминаем первое число.
2. Следующее число последовательности сравниваем с числом, лежащим в М. Записываем в М большее из этих чисел (т. е. либо сохраняем в М прежнее число — если оно больше, — либо записываем вместо него следующее).
3. Повторяем шаг 2 до конца данной последовательности.
Сразу же возникают вопросы, которые можно разделить на две группы (хотя они и связаны).
Вопросы к постановке задачи:
а) Каково представление
чисел, т. е. представлены ли они целыми
числами, десятичными дробями
(действительными числами), простыми
дробями или арифметическими выражениями
типа
 ?
Непосредственно можно сравнивать только
целые или действительные числа. Поэтому
если в исходной последовательности
встречаются арифметические выражения
(а простые дроби — это тоже арифметические
выражения, содержащие только операцию
деления), то их сравнению должно
предшествовать их вычисление, т. е.
к предлагаемому алгоритму добавится
еще ряд шагов.
?
Непосредственно можно сравнивать только
целые или действительные числа. Поэтому
если в исходной последовательности
встречаются арифметические выражения
(а простые дроби — это тоже арифметические
выражения, содержащие только операцию
деления), то их сравнению должно
предшествовать их вычисление, т. е.
к предлагаемому алгоритму добавится
еще ряд шагов.
б) Что значит "найти максимальное число" — просто дать его значение или, кроме того, указать еще и его место в последовательности? Предлагаемый метод решения дает только значение. Если нужно указывать место числа, то числа последовательности нужно как-то нумеровать или именовать, а метод решения изменить. Кроме того, как быть, если найдено несколько одинаковых максимальных чисел — указывать все их места или, например, первое по порядку?
Ответы на эти вопросы неоднозначны. Дать их может только тот, кто ставит задачу. Предположим, что в нашем случае ответы таковы: числа — целые и кроме значения результата нужно указать еще и номер первого по порядку максимального числа, поэтому числа последовательности должны быть как-то пронумерованы.
Вопросы к методу решения:
а) Как искать следующее число? В длинной последовательности это требует аккуратности даже при ручной работе. Можно, например, зачеркивать или как-то удалять уже просмотренные числа, и тогда следующее число — это первое незачеркнутое, а можно иметь некоторый указатель, работать с числом, на которое он указывает, а потом передвинуть его на следующее число. Поскольку уже решено, что числа последовательности будут пронумерованы, то таким указателем может служить специальная переменная — счетчик номеров, значение которой после каждого сравнения увеличивается на единицу.
б) Как определить конец последовательности? Есть два стандартных способа: либо при ее вводе указать количество ее элементов (чисел), либо ввести дополнительный элемент — признак конца. Остановимся на первом варианте.
Теперь описанный выше процесс можно описать более точно. Для записи чисел в память будем пользоваться обычным для языков программирования оператором присвоения. Например, М: = х означает, что переменной М присвоено значение переменной х; в терминах машинной памяти это значит, что в ячейку памяти М записано содержимое ячейки х.
1. Ввести данные: исходную последовательность расположить в ячейках р(1), ..., р(п).
1. е: = п (в ячейке е лежит число элементов последовательности).
3. i:= 1 (счетчик номеров устанавливаем в начальное положение).
4. М: =р(1) (в М — первое число).
5 .N:=1 (в N — его номер).
6. i: =i + 1 (счетчик увеличивается на 1).
7. Если
 ,то
перейти к п.10; иначе перейти к следующему
шагу (п. 8).
,то
перейти к п.10; иначе перейти к следующему
шагу (п. 8).
8. М: =p(i) (в М — новое число ).
9. N:=i (в N — его номер).
10. Если i < е, то перейти к п. 6; иначе — к следующему шагу.
11. Конец алгоритма.
Это описание уже близко к программе на языке программирования. Для машинной реализации остается выбрать язык программирования, уточнить с его помощью шаг 1 (он не элементарен и в разных языках будет уточнен по-разному),
вставить после шага 10 шаг, связанный с выводом результата (на печать или экран), и записать алгоритм на выбранном языке, строго соблюдая его синтаксис.
Алгоритм является фундаментальным понятием информатики. Можно выделить три крупных класса алгоритмов: вычислительные, информационные и управляющие. Вычислительные алгоритмы, как правило, работают со сравнительно простыми видами данных (числа, матрицы), но сам процесс вычисления может быть долгим и сложным. Информационные алгоритмы представляют собой набор сравнительно простых процедур (например, поиск числа или слова, удовлетворяющего определенным признакам), но работающих с большими объемами информации. Таковы алгоритмы в различных базах данных. Для того чтобы они работали эффективно, важно иметь хорошую организацию данных. Например, чтобы в картотеке можно было быстро найти нужные сведения, эти сведения нужно постоянно поддерживать в определенном порядке (по разделам, внутри разделов по алфавиту и т. д.). Управляющие алгоритмы характеризуются тем, что данные к ним поступают от внешних процессов, которыми они управляют. Результаты работы этих алгоритмов представляют собой различные управляющие воздействия. Поэтому значения данных в ходе работы управляющих алгоритмов меняются (иногда очень быстро), и алгоритм должен вовремя правильно отреагировать, т. е. выдать нужный управляющий сигнал в нужный момент.
Блок-схема алгоритма
Такие схемы используются в программировании весьма широко. Они позволяют представить алгоритмы в обозримом виде, что дает возможность анализировать их работу, искать логические ошибки в процедуре их реализации и т. п.
Блок-схема представляется в виде графа специального вида. Вершины графа соответствуют определенным частям алгоритмов (в предельном случае отдельным шагам алгоритма или командам вычислительной машины), а дуги показывают возможные переходы между этими вершинами в процессе выполнения алгоритма.
Безусловные шаги принято изображать прямоугольниками, условные шаги — ромбами. Из ромба всегда выходят две стрелки: одна имеет пометку "да" (условие выполнено), другая — пометку "нет" (условие не выполнено). Граф, изображенный на рис. 1, соответствует процессу отыскания максимального числа в последовательности, который описан в статье "Алгоритм".
Процесс выполнения
алгоритма представляется в графе
как путь из начальной вершины в конечную.
Если все шаги алгоритма — безусловные,
то этот путь при любых данных одинаков,
хотя результаты, разумеется, могут
быть различными. 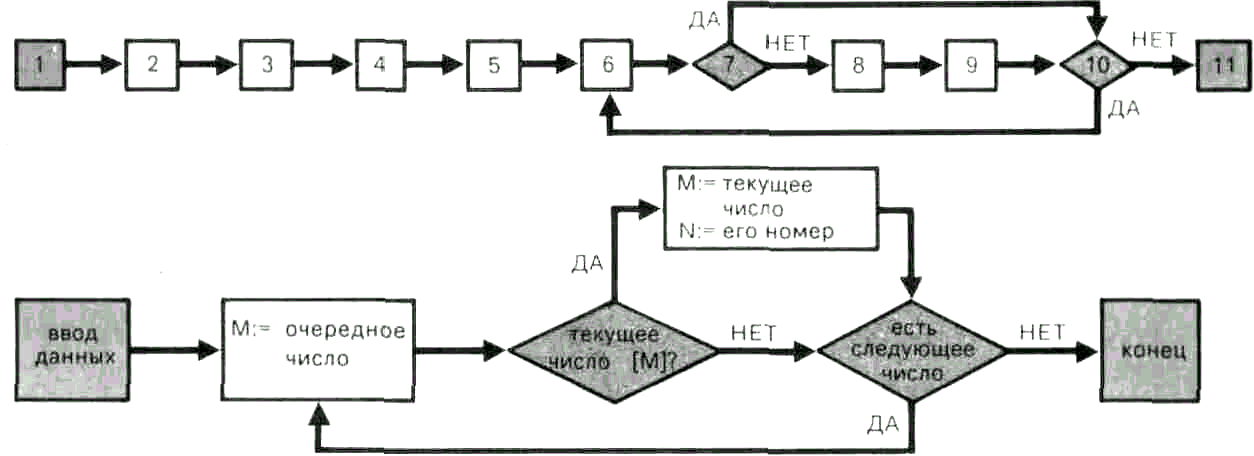
Рис.1.
Рис.2.
Если же в алгоритме есть условные шаги (а чаще всего так и бывает), то путь зависит от выполнения содержащихся в них условий. Как правило, алгоритм содержит циклы, т. е. замкнутые пути, возвращающиеся в пройденную ранее вершину. Алгоритм на нашем рисунке содержит цикл между шагами 6 и 10, который разветвляется в шаге 7.
Поэтому возможны два варианта прохождения цикла 6, 7, 8, 9, 10, 6 и 6, 7, 10, 6. Цикл обязательно содержит условную вершину, в которой можно выйти из цикла. В данном примере такой вершиной является шаг 10. Выход из цикла происходит, когда все числа последовательности просмотрены. Если условия выхода из цикла сформулированы неправильно, то может оказаться, что они никогда не выполняются, и процесс исполнения алгоритма становится бесконечным (он, как говорят, зацикливается, что является типичной программистской ошибкой).
Для компактного описания циклов в языках программирования имеются специальные операторы циклов. Основную часть нашего примера (шаги 2 — 10) с помощью такого оператора можно записать гораздо короче. Правда, оператор цикла нельзя считать элементарным шагом, в частности, потому, что время его выполнения зависит от исходных данных и может быть сколь угодно большим.
Элементарность шагов входит в число необходимых требований к алгоритмам. Однако уже на нашем простом примере видно, что строгое соблюдение этого требования весьма обременительно — описание алгоритма разрастается и становится плохо обозримым. Выход заключается в том, что шаги надо укрупнять, но при условии, что они в дальнейшем будут доведены до элементарных.
Крупный шаг — это фактически алгоритм, являющийся частью (подалгоритмом) более сложного алгоритма. Такие подалгоритмы называются блоками. Блок обычно не элементарен (его размеры неограниченны и выбираются произвольно). Однако правильно сформулированный блок обладает всеми другими признаками алгоритмического шага. В частности, он имеет точно выделенное начало (точку входа) и может быть условным или безусловным. У безусловного блока — всегда одна точка выхода. Условный блок имеет несколько точек выхода (их может быть больше двух, если блок содержит несколько условий). Другие блоки алгоритма связаны с данным блоком только через точки входа и выхода. Поэтому если блок правильно решает свою задачу, т. е. всегда дает нужный результат, то его внутренняя структура несущественна для остальной части алгоритма. Из этого следуют два важных вывода. Во-первых, описание алгоритма можно представлять в укрупненном блочном виде. Отсутствие детального описания внутренней структуры блоков не мешает пониманию того, как работает алгоритм в целом; важно лишь, чтобы было четко определено, какие блоки запускают данный блок в работу, где лежит его исходная информация, где будет записан результат и куда переходить после окончания его работы. Такое блочное представление особенно удобно на первых этапах разработки алгоритмов (детализация блоков происходит позднее). Во-вторых, детализацией разных блоков (т. е. программированием — доведением их до настоящих алгоритмов и программ) могут заниматься разные люди независимо друг от друга. Это важно при организации работ по созданию сложных программ.
Блок-схемы являются частным случаем наглядных форм представления алгоритмов. Существуют и другие способы представления: операторные алгоритмы, диаграммы смены состояний и т. п. Развивается и теория таких представлений. С ней можно познакомиться в статье «Схема алгоритма».
Схема алгоритма
Запись алгоритма на каком-нибудь языке программирования для человека, профессионально не занимающегося решением задач на ЭВМ, выглядит как непонятный набор символов. Но часто бывает необходимо, чтобы именно такой человек смог оценить семантику того процесса, который реализуется на машине. Это, например, необходимо при внедрении программных систем в различные сферы планирования, управления, проектирования и т. п. Конечный пользователь, которому предстоит иметь дело с системой, как правило, хотел бы на понятном ему уровне и наглядно получить информацию о сути тех алгоритмов, с которыми он будет работать.
Для решения этой задачи часто используют блок-схемы, позволяющие весьма наглядно представлять алгоритмы и построенные на их основе программы для компьютеров. Для примера на рис. 1 показана блок-схема алгоритма поиска наибольшего общего делителя двух натуральных чисел. На этой блок-схеме прямоугольники соответствуют
 Рис. 1
Рис. 1
вычислениям, ромбы
— логическим проверкам, а треугольники
— вводу исходных данных и выводу
результатов.
Кроме блок-схем
используются и другие способы
отображения структуры алгоритмов и
программ. Но они получили гораздо меньшее
распространение, чем блок-схемы.
Правда, для теоретических исследований
в начале развития теории программирования
использовались специальные операторные
схемы алгоритмов, предложенные советским
исследователем А. А. Ляпуновым. На
рис. 2 тот же алгоритм поиска наибольшего
общего делителя двух натуральных чисел
представлен в виде записи через операторы
Ляпунова. Буквами Аi
обозначены
вычислительные операторы, Рi
— логические
операторы, Фi
— операторы ввода, Оi
— операторы
вывода, S
— оператор прекращения алгоритма,
 — операторы безусловного перехода.
Выполнение операторов происходит слева
направо в порядке их
написания. Если очередной оператор есть
Р„ то при отрицательном результате
проверки начинает выполняться соседний
правый в записи оператор. При положительном
результате проверки условия происходит
переход по стрелке. При выходе на оператор
— операторы безусловного перехода.
Выполнение операторов происходит слева
направо в порядке их
написания. Если очередной оператор есть
Р„ то при отрицательном результате
проверки начинает выполняться соседний
правый в записи оператор. При положительном
результате проверки условия происходит
переход по стрелке. При выходе на оператор
 всегда происходит переход по стрелке.
При сложных алгоритмах стрелки,
характеризующие переходы, целиком не
рисуются, чтобы не загромождать схему,
рисуется лишь начало и конец стрелки,
помечаемые одинаковыми номерами, а
сами стрелки пишутся в той же строке,
что и операторы. Такая запись показана
на рис. 2, но ниже первой.
всегда происходит переход по стрелке.
При сложных алгоритмах стрелки,
характеризующие переходы, целиком не
рисуются, чтобы не загромождать схему,
рисуется лишь начало и конец стрелки,
помечаемые одинаковыми номерами, а
сами стрелки пишутся в той же строке,
что и операторы. Такая запись показана
на рис. 2, но ниже первой.
