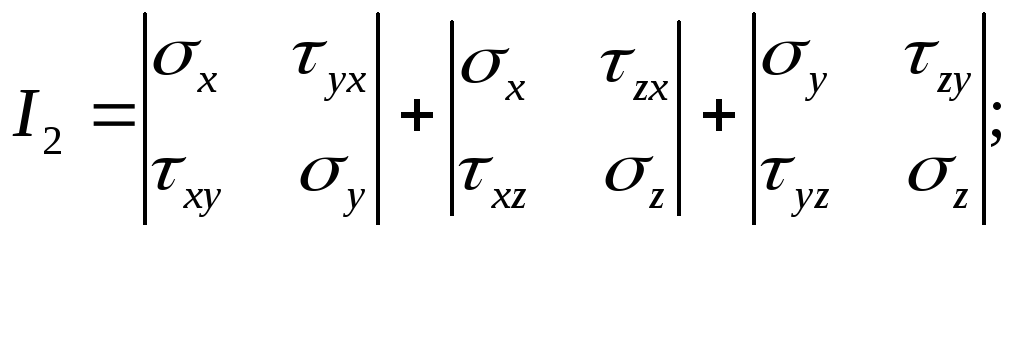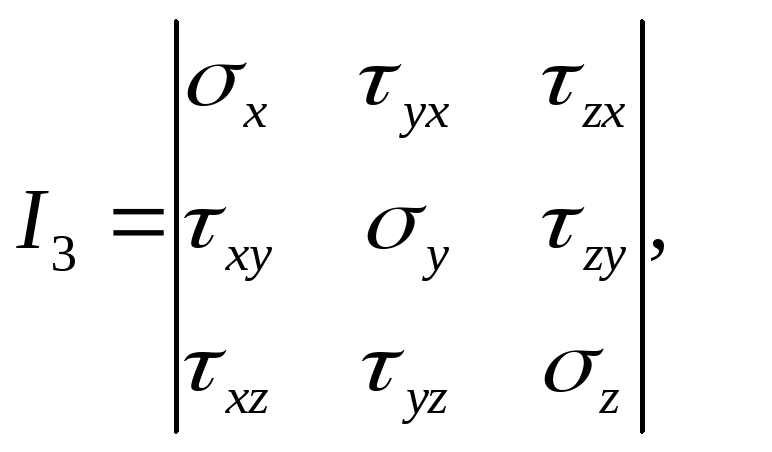9.3.4 Визначення положення головних площадок та значень головних нормальних напружень в загальному випадку складного напруженого стану

Нехай відомі та на трьох похідних взаємно перпендикулярних площинках, що проведені через досліджувану точку (рис. 9. 17,в). Необхідно визначити положення Г.П., тобто напрямні косинуси нормалей до них [] та значення Г.Н.Н. на цих площадках.

Розв’язання.

Припустимо, що нахилена площинка (рис. 9.17,в) є головною, тобто на ній , а повне напруження буде головним, тобто . В цьому разі проекції головного напруження на похідні вісі x, y, z будуть такими:

Підставивши ці вирази в попередню формулу перетворення векторів напружень (9.17) та зробивши відповідні перетворення, отримаємо

(9.18)

Щоб знайти тепер 4 невідомі (l, m, n та σ), необхідно скласти ще одне рівняння. Як відомо (з лінійної алгебри) сума квадратів напрямних косинусів вектора в просторі дорівнює одиниці. Розв’язуючи рівняння (9.18) відносно невідомих l, m, n, можна визначити положення Г.П. Нульові розв’язки l=m=n=0 неможливі внаслідок відомого співвідношення між напрямними косинусами:

^.

Як відомо, система лінійних однорідних рівнянь має ненульове рішення в тому випадку, коли визначник, складений з коефіцієнтів при невідомих, дорівнює нулю, а саме:

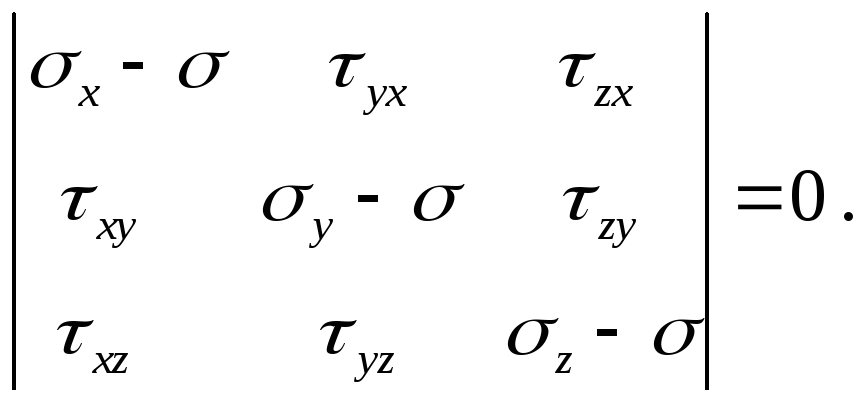
Розкриваючи визначник, позначивши при цьому незмінні (інваріантні) складові частини загального рішення літерами :

отримаємо таке кубічне рівняння для головних напружень:

.

(9.19)

В цьому рівнянні коефіцієнти – так звані інваріанти напруженого стану в точці, коли самі компоненти можуть змінюватись при повороті площин, але такі їх комбінації – постійні незалежно від орієнтації площинок.

Розв’язання кубічного рівняння дає три дійсних корені, які і є трьома головними напруженнями що виникають на трьох взаємно перпендикулярних головних площадках; при цьому (в алгебраїчному розумінні).

Для визначення напряму будь-якої головної площадки (наприклад, першої) необхідно в систему рівнянь (9.18) підставити значення відповідного головного напруження (наприклад, першого ) та розв’язати ці рівняння відносно .

Найбільше дотичне напруження при будь-якому об’ємному стані виникає на площадках, паралельних головному напруженню і рівно нахилених (під кутом 45˚) до головних напружень та , причому , а нормальні напруження на цих площадках дорівнюють половині суми відповідних головних.

Загальна класифікація напружених станів

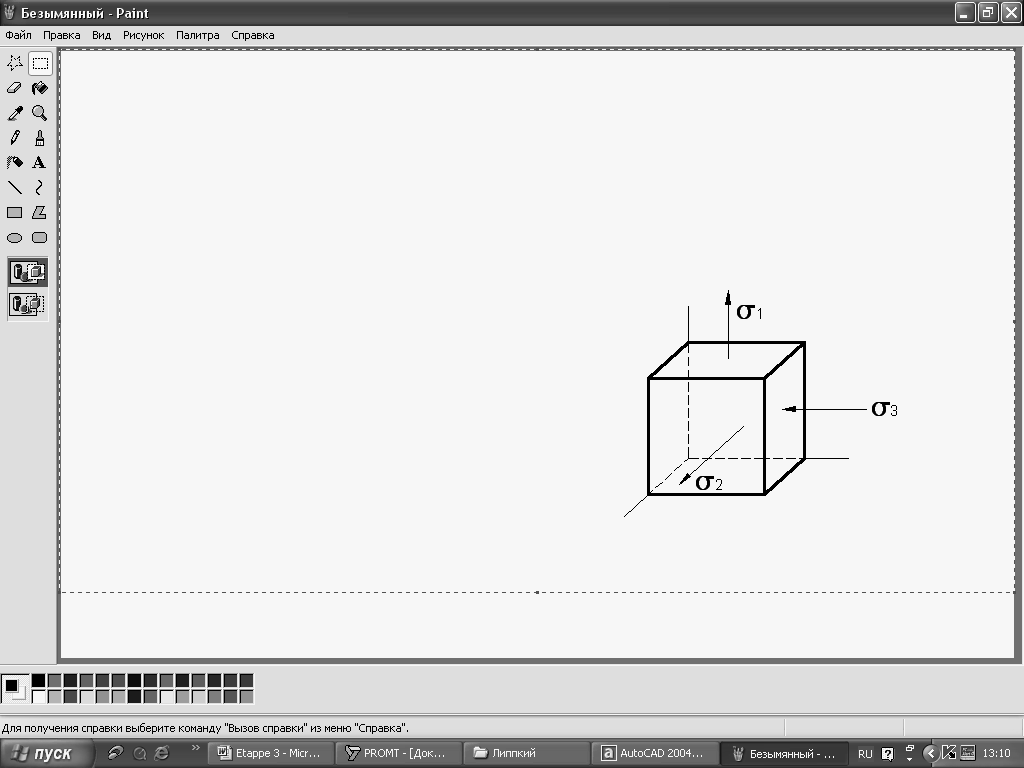
Якщо всі три інваріанти напруженого стану ненульові, то всі три корені кубічного рівняння (9.19) дійсно ненульові, а напружений стан в точці буде тривісним (об’ємним – рис.9.18, в). Так, в точках тіла зануреного глибоко в воду, має місце рівномірне тривісне стискання.

Якщо один з інваріантів Н.С. – нульовий (наприклад I₃=0), то кубічне рівняння спрощується, його розв’язання дає два ненульові корені, і напружений стан в точці буде двовісним, або плоским (рис. 9.18, с). Приклади такого Н.С.: в точках тонкостінних оболонок під дією внутрішнього тиску; в тонких дисках, що швидко обертаються; в стержнях при їх чистому крученні, та в інших випадках складного опору.

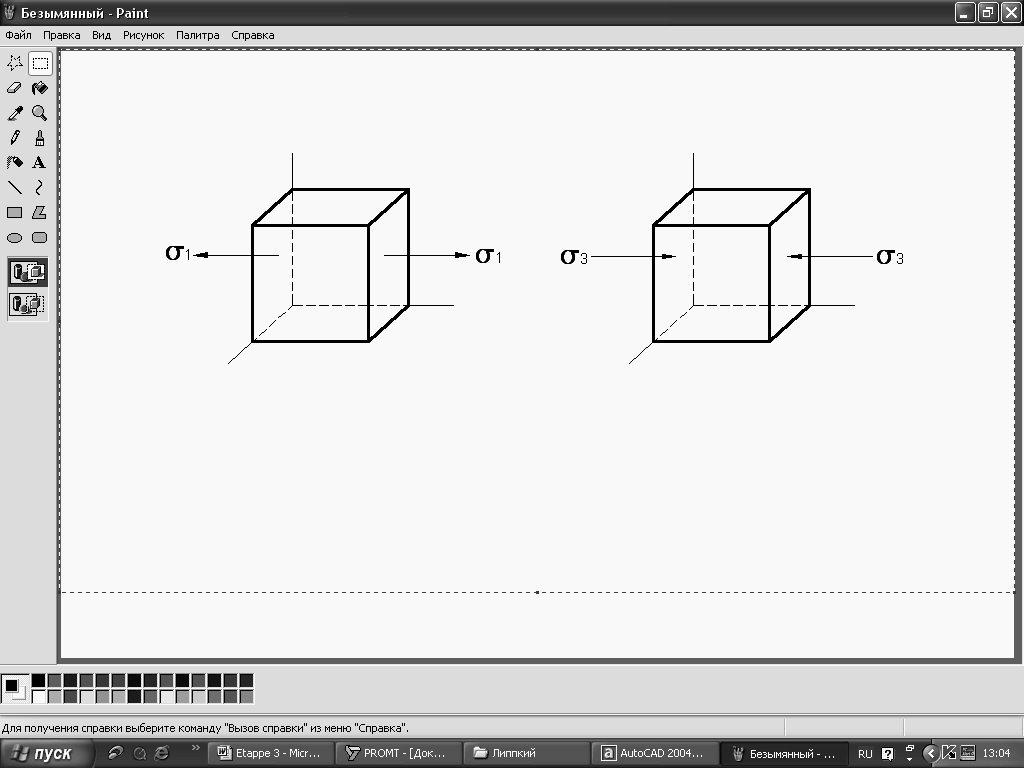
Якщо два інваріанти напруженого стану нульові (наприклад: ), то кубічне рівняння після скорочення стане лінійним і матиме при розв’язуванні лише один корінь, тобто одне головне напруження або . Напружений стан при цьому – лінійний, одновісний. Приклад: при розтягу – стиску (рис. 9.18, а) та при чистому згинанні.

а
в	с

Рисунок 9.18 – Види напруженого стану:

а – лінійний; в – просторовий; с – плоский

Узагальнюючи все сказане, можна запам’ятати просто: в залежності від наявності головних нормальних напружень на трьох головних площинках, що проходять через точку, напружений стан в довкіллі точки може бути складним (дво- тривісний) чи простим (одновісний, лінійний).