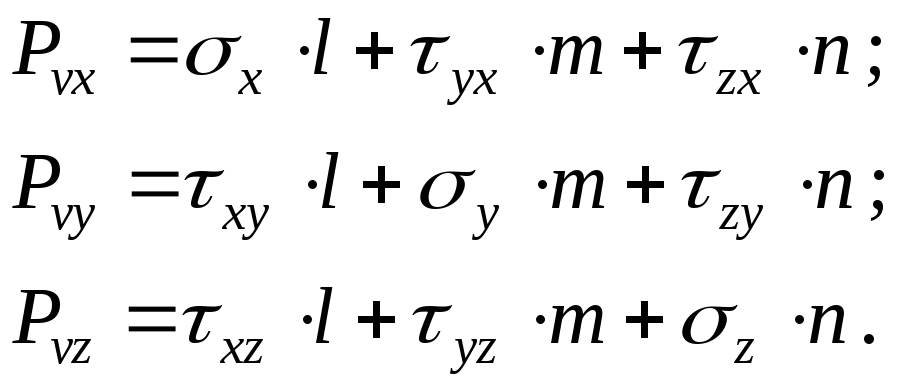9.3.2 Визначення напружень на площадках довільного положення
Якщо трійка ортогональних сікучих площин буде зорієнтована інакше, ніж на рис. 9.16, то складові тензора напружень будуть іншими. Їх можна визначити з рівнянь рівноваги частини паралелепіпеда, відсіченої цими нахиленими площинами.
Спочатку
проведемо через точку Т
в центрі паралелепіпеда (рис. 9.17) похилу
площину з нормаллю
,
напрямні косинуси якої відносно похідних
осей x, y, z
позначимо так:
Вектор
повного напруження
на цій площині розкладено на три складові
частини паралельні похідним осям:
Відокремлений таким чином чотирьохгранник
(тетраедр) має бути в рівновазі під дією
сил пружності, що виникли на його гранях.
Проектуючи всі ці сили на осі x, y, z та
враховуючи співвідношення площин граней
тетраедра:
можна отримати складові повного
напруження
на площині
:
|
|
(9.17) |
Таким чином, з’ясовано, що напружений стан в точці визначається повністю тензором напружень, отриманих для будь-якої похідної трійки взаємно перпендикулярних площинок, проведених через досліджувану точку.
|
|
||
|
а |
б |
в |
Рисунок 9.17 – Нахилена площина загального положення (a); вектори напружень на довільних площинах тетраедра (б) та на головній нахиленій площині (в)
Далі
можна визначити повне напруження на
довільно нахиленій площині АВС:
його проекції на нормаль до цієї площини
та повне дотичне напруження
Отримані співвідношення (9.17) показують, що в залежності від нахилу сікучої площини напруження змінюються.
Можна
доказати, що існує така трійка ортогональних
площадок, проведених через розглядувану
точку, на яких дотичні напруження
відсутні (при розтяганні це має місце
при
;
і при
).
При цьому нормальні напруження на них
– екстремальні, що й необхідно знати
для оцінки міцності.
9.3.3 Головні площадки та головні напруження
Простіше
всього та дохідливо уявити їх можна на
прикладі осьового розтягання бруса
(рис. 9.14), де напруження на нахиленій під
кутом
площині 2 визначались як
,
де
– напруження в поперечному перерізі
бруса. Як видно з цих формул при
:
а
є найбільшим; при
:
і
– найменше.
Ті площинки, на яких відсутні дотичні напруження, назвали головними площинами (Г.П.), а нормальні напруження на них – головними нормальними напруженнями (Г.Н.Н.).
Завдяки
періодичності функції синуса (
)
можна уявити три Г.П., що проходять через
точку: перша (при
)
– перпендикулярна до поздовжньої вісі
бруса; друга – (при
)
– паралельна поздовжній осі бруса;
третя (як і друга) – але в самій площині
рисунка (рис. 9.14,г).
Нормальні
напруження на головних площинах –
екстремальні; при розтязі це:
Найбільші
ж дотичні напруження виникають при
розтязі (стиску) бруса на площинах,
нахилених під кутом
до поздовжньої осі бруса і дорівнюють
.
Це підтверджує і той факт, що зсув та
сколювання стиснутих чавунних зразків
проходило на площинах цього напряму,
оскільки крихкі матеріали протистоять
зсуву дуже слабко.
Якщо з трьох головних напружень тільки одне не дорівнює нулю, то напружений стан називають лінійним (одновісним); якщо виникають два головні нормальні напруження, то напружений стан є плоским (двовісним); коли ж наявні всі три головні напруження, напружений стан – об’ємним (тривісним). Лінійний напружений стан називають простим, а плоский та об’ємний – складними.
З
наведених формул можна встановити та
неважко уявити, що при розтяганні,
стисканні та чистому згинанні напружений
стан в усіх точках поперечного перерізу
буде одновісним, з одним лише головним
напруженням на першій, поперечній
головні площинці (при
);
на двох інших ортогональних площинках
(при
)
нормальні напруження відсутні.