2. Системы линейных алгебраических уравнений

2.1. Основные понятия

Определение 2.1.1.

Системой m линейных алгебраических уравнений с n-неизвестными х₁ х₂ … х_n

называется система вида:

(2.1)

где a_ij – коэффициенты системы, b_i - свободные члены , , .

Первый индекс у коэффициентов указывает на номер уравнения, второй на номер неизвестного.

Определение 2.1.2.

Решением системы (1) называется совокупность

чисел (х₁⁰, х₂⁰ , … х_n⁰) подстановка которых в систему вместо неизвестных обращает все уравнения в тождества .

Определение 2.1.3.

Система у которой нет ни одного решения , называется не совместной . Совместной называется система , имеющая хотя бы одно решение. Совместная система , имеющая единственное решение называется определенной , в противном случае неопределенной .

Рассмотрим другие формы записи системы (2.1) ,для чего введем обозначения:

Матрицу А называют основной матрицей системы , матрицы b_mx1, x_nx1 принято называть вектором свободных членов и вектором неизвестных.

Легко убедиться , что умножение матрицы А на вектор Х по правилу умножения двух матриц дает левую часть системы (2.1.). Поэтому произведение АX является столбцовой матрицей тех же размеров, что и матрица B. Поэтому систему записывают в форме матричного уравнения.

(2.1.)ЫАX=b

Следующая запись связана с операцией сложения:

Если i-ый столбец обозначить через Аⁱ то то более кратко :

А¹х₁+ А²х₂+…+ Аⁿх_n= b

Отсюда видно ,что решить систему это значит разложить правую часть по столбцам.

Определение 2.1.4.

Две системы с одинаковым числом неизвестных называются эквивалентными , если множество решений одной системы совпадает с множеством решений другой системы.

Система (2.1) может иметь 0, 1 или Ґ много решений.

2.2 Крамеровские системы

Определение 2.2.1.

Система линейных уравнений называется крамеровской , если основная матрица системы квадратная и невырожденная, т.е. А_nxn ,

Теорема 2.2.1.

Крамеровская система совместна и имеет единственное решение.

Доказательство:

А_nxn , , то для А$ А^-1 Используем запись АX=в Ы А^-1Ах=

А^-1вЮIX = А^-1в Ю X = А^-1в

Докажем единственность решения.

Пусть х и у два решения Ю Аx=в и Ау=вЮ Ах= АуЮ А^-1Ах=

А^-1АуЮх=у

Доказывая теорему мы получили способ решения системы который называется матричным. Из него можно получить формулы Крамера

Поскольку :

Ю

(2.2)

Di - определитель, полученный из определителя матрицы A заменой i столбца столбцом свободных членов системы.

Di-можно получить используя разложения по i-му столбцу .

Формулы называются формулами Крамера, они используются для систем небольшого порядка .

Пример 2.2.1. Решим матричным способом систему:

Решение: Вычислим определитель основной матрицы системы

detA=100 Вычислим алгебраические дополнения всех элементов основной матрицы ,

и т.д.

где - любые действительные числа

Пример 2.2.2. Решить по формулам Крамера систему уравнений:

Решение: Вычислим определитель системы:

Найдем вспомогательные определители:

Ответ: {1;2;3}.

2.3 Системы линейных уравнений общего вида

При решение системы прежде всего нужно выяснить ее совместность. Ответ на этот вопрос дает теорема Кронекера-Капелли.

Определение 2.3.1.

Пусть дана система m-уравнений с n – неизвестными АX=В

Матрица вида :

= (A/B)

Называется расширенной матрицей системы линейных уравнений .

Теорема 2.3.1. (критерий совместности )

Система АX=В совместна тогда и только тогда , когда (rangА= rangB) ранг основной матрицы системы равен рангу расширенной матрицы.

Доказательство:

Необходимость.

Если система совместна , то $(x₁⁰… x_n⁰): А¹х₁⁰+ А²х₂⁰+…+ Аⁿх_n⁰= b

т.е. b- есть линейная комбинация столбцов матрицы А и по Теореме 1.8 rangA= rang(A/b)

Достаточность.

Если rangА= rangB=r то выберем в А базисный минор М_r№0 этот же минор будет базисным в матрице В. Применим теорему о базисном миноре . По этой теореме столбец ''B,, есть линейная комбинация базисных столбцов т.е. ''В,, есть линейная комбинация столбцов матрицы А следовательно система совместна.

Итак, если rangA№rang(A/b) то системаАX=В несовместна. Пусть теперь А_mxn, (А/В)_mx(n+1) основная и расширенная матрицы системы и rangА= rang(А/В) =r=min(m,n) т.е. А матрица полного ранга .Возможны следующие случаи :

1)m=n т.е. число уравнений равно числу неизвестных , такая система будет крамеровской .

2)m>n, тогда r(A)= r(A/в)=n, (m-n) уравнений является линейной комбинацией n-уравнений , входящих в базисный минор . Отбрасывая эти (m-n) уравнений , получаем крамеровскую систему

Пример 2.3.1. Решить систему:

Решение:

Легко убедиться , что r(A)=r(A/b)=3 n<m=4 4-3=1

Одно уравнение является лишним. Взяв первые три уравнения, коэффициенты при которых входят в базисный минор, получаем крамеровскую систему рассмотренного выше случая .

Отбрасывание лишних уравнений основано на том, что линейная комбинация тождеств есть снова тождество

3) m<nЮ r(A)= r(A/в)=m и система имеет (n-m)- переменных для однозначного определения которых хватает (n-m) уравнений. Для решения системы выделим в матрице A базисные столбцы:

Все неизвестные, коэффициенты которых вышли в базисный минор M_r называются закреплёнными неизвестными, остальные (n-r)= (n-m) переменных – свободными .Данная система эквивалентна системе:

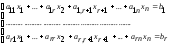
Перенося в правую часть слагаемые со свободными переменными, получим систему в виде:

Если теперь придать некоторые значения свободным переменным, то получим крамеровскую систему. Подчеркнём, что свободным переменным можно придать бесконечное множество значений и следовательно получить бесконечное множество решений системы. Для выяснения сути изложенного рассмотрим систему:

Пример 2.3.2.

Поскольку r(A)= r(A/в)=3 то 4-3=1 переменных являются свободными. Пусть базисными являются первые три столбца Ю x₁ ,x₂ ,x₃ закреплённые переменные, x₄ – свободная переменная Перенося четвёртый столбец в правую часть, имеем :

И используя решение примера 2.2.1., получаем

Это общее решение системы в виде

x_i=f( x₄ )

Задавая x₄ различные значения, будем получать различные частные решения системы. Очевидно таких решений бесчисленное множество .

4)пусть теперь r(A)= r(A/в)= r< min(m,n)Ю r< m и (m-r)- уравнений является линейной комбинацией остальных уравнений. Отбрасывая эти уравнения приходим к рассмотренным ранее случаям.