1.3.Транспонирование матриц

Определение 1.3.1. Пусть дана матрица А=а.Матрица

А=(a) называется транспонированной по отношению к матрице А(если ее строки являются столбцами матрицы А и наоборот).

Если: a=a; ; .

Это соотношение показывает, что для того чтобы получить матрицу А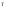 нужно в исходной матрице А строки заменить столбцами или столбцы строками.

Например: A==>A=

A==>A=.

Операция транспонирования обладают следующими свойствами:

1. (A+B) =A+B, A, B.

2. (A)=A, , A.

3. (AB)=BA.

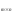4. (A)=A.

Определение 1.3.2. Матрица А называется нормальной, если

АА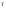=АА.

Определение 1.3.3. Матрица А называется симметричной, если А=А; a=a; ; .

Если А=(-А);a=(-a); ;. то матрица кососимметричная.

Определение 1.3.4. Матрица А называется ортогональной, если:

AA=AA=I.

Замечание. Данные определения применяют только к квадратным матрицам.

Контрольные вопросы и задания.

1. Что называется матрицей?

2. Какие матрицы называются равными?

3. Можно ли сказать, что определитель n –го порядка есть число?

4. Что называется определителем n-го порядка?

5. Существует ли определитель матрицы ?

6. Что понимается под операцией транспонирования матрицы?

7. В каком смысле столбцы и строки матрицы равноправны?

8. По какому правилу складываются матрицы.

9. Можно ли сложить две матрицы с размерами 2 x 3 и 3 x 1?

10. Можно ли из одной матрицы вычесть другую матрицу? Как это сделать? Каким условиям должны удовлетворять при этом матрицы? Какие размеры имеет при этом матрица, являющаяся результатом этой операции?

11. Как умножить матрицу на число?

12. Пусть M – множество всех матриц размером 5 x 4, элементы которых принадлежат полю K рациональных чисел. Корректна ли на множестве M операция умножения матрицы A из M на число из поля K₀ , т.е. поля всех действительных чисел?

13. Как перемножаются матрицы?

14. Можно ли умножить матрицу с размерами 2 x 3 на матрицу с такими же размерами?

15. Каковы размеры матрицы A, если известно, что (1 2 3)A = (0 1)?

16. Приведите примеры строки A и столбца B , для которых существует произведение : a) AB; б) BA; в) AB и BA ; г) AB, BA и AB=BA.

17. Какими свойствами обладает операция умножения матриц ?

18. Какая матрица выполняет роль единицы в операции умножения матриц с размерами n x n ? Сколько таких матриц имеется во множестве всех матриц с размерами n x n ?

Задачи и упражнения для самостоятельной работы.

1. Докажите справедливость следующих свойств матриц:

a)

б) (A+B)^T=A^T + B^T; в) (AB)^T = B^TA^T .

2. Даны матрицы A и B:

а) ; б) ;

Вычислите: 1⁰) AB ; 2⁰) BA . Сравните матрицы AB и BA .

3. Даны матрицы A и B:

а) ,

б) .

Вычислите: 1⁰) AB; 2⁰) A^TB^T; 3⁰) B^TA^T .

3. Вычислите матрицу AB и сравните ее с матрицей A, если

.

3. Вычислите матрицу AB и сравните ее с матрицей B, если

.

3. Вычислите матрицу AB и сравните ее с матрицей B . Какая элементарная операция над строками матрицы B равносильна умножению этой матрицы слева на матрицу A ?

а) ;

б) .