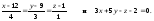- •Основы линейной, векторной алгебры и аналитической геометрии
- •Содержание.
- •Обозначения, используемые в пособии.
- •1.3.Транспонирование матриц
- •Операция транспонирования обладают следующими свойствами:
- •1.4. Понятие определителя.
- •1.5. Минор. Теорема Лапласа. Определение 1.5.1.
- •Свойства определителей
- •1.7 Обратные матрицы
- •Достаточность: Пусть Рассмотрим элементы с определяются как
- •4)Обратная матрица единственна
- •1.8 Ранг матрицы Определение 1.8.1.
- •Определение 1.8.2.
- •2. Системы линейных алгебраических уравнений
- •2.1. Основные понятия
- •2.2 Крамеровские системы
- •Пример 2.2.2. Решить по формулам Крамера систему уравнений:
- •2.3 Системы линейных уравнений общего вида
- •2.4 Однородные системы линейных уравнений
- •Пример 2.4.1 Решить систему:
- •3. Основы численных методов решения задач теории матриц и систем линейных алгебраических уравнений .
- •3.1 Элементарные преобразования матриц
- •Действительно:
- •3.2 Вычисление определителя
- •3.3 Вычисление ранга матрицы
- •3.4 Решение систем линейных уравнений
- •3.5 Нахождение обратной матрицы.
- •4. Линейные векторные пространства
- •4.1 Понятие линейного пространства
- •4.2 Линейная зависимость системы векторов
- •4.3. Базис и размерность линейного пространства.
- •4.4. Координаты вектора
- •Пример 4.4.1.
- •4.5. Евклидово пространство
- •4.6. Ортогональность векторов в Еп.
- •5. Вектора в трёхмерном пространстве .
- •5.1. Угол между двумя векторами. Проекция вектора на ось.
- •5.2. Координаты вектора заданного двумя точками.
- •5.3.Условие коллинеарности двух векторов в координатной форме
- •5.4. Скалярное произведение векторов в координатной форме
- •5.5. Определение длины вектора и угла между двумя векторами.
- •5.6. Направляющие косинусы вектора
- •5.7. Векторное произведение двух векторов
- •5. 8. Смешанное произведение трех векторов
- •5.9. Свойства смешанного произведения
- •Элементы аналитической геометрии.
- •6.1. Прямая на плоскости.
- •Уравнение прямой в отрезках
- •6.2.3. Уравнение плоскости в отрезках
- •6.2.4. Уравнение плоскости проходящей через три точки
- •6.2.5.Угол между двумя плоскостями
- •6.2.6. Условия перпендикулярности и параллельности плоскостей
- •6.2.7. Расстояние от точки до плоскости
- •6.3. Прямая линия в пространстве r3
- •6.3.1. Векторное уравнение прямой
- •6.3.2. Канонические уравнения прямой
- •6.3.3. Прямая как линия пересечения двух плоскостей
- •6.3.4. Угол между двумя прямыми
- •6.3.5. Условия параллельности и перпендикулярности прямых
- •6.4. Прямая и плоскость в пространстве
- •6.4.1. Пересечение прямой и плоскости в пространстве r3
- •6.4.2.Условие параллельности и перпендикулярности прямой и
- •6.4.3.Угол между прямой и плоскостью
- •7. Кривые второго порядка
- •7.1.Окружность
- •7.2. Эллипс
- •7.3.Гипербола
- •7.4.Парабола
- •7.5. Уравнения кривых второго порядка с осями симметрии параллельными осям координат.
- •8. Поверхности второго порядка
- •8.1.Цилиндрические поверхности с образующими, параллельными координатной оси
- •8.2.Цилиндры второго порядка
- •8.3.Поверхности вращения
- •8.4. Поверхности второго порядка заданные каноническими уравнениями
- •8.4.1. Эллипсоид
- •8.4.2.Гиперболоиды
- •8.4.3. Параболоиды Эллиптический параболоид.
- •Гиперболический параболоид.
- •8.4.4. Конус второго порядка
- •9. Расчетные задания.
- •9.1. Линейная и векторная алгебра.
- •9.2. Аналитическая геометрия.
- •10. Тестовые задания для самостоятельной работы.
- •Задание 3. Найдите матрицу х из уравнений:
- •Задание 4. С помощью формул Крамера решить систему уравнений:
- •Задание 9. Найти координаты вектора векторного произведения векторов a и b.
- •2. Найти точку пересечения прямой и плоскости.
6.4. Прямая и плоскость в пространстве
Для определения взаимного расположения прямой и плоскости в пространстве достаточно установить, параллельна ли прямая lплоскости или нет. Если нет, то в какой точке пересекает ее и под каким углом.
6.4.1. Пересечение прямой и плоскости в пространстве r3
Пусть в пространстве R3 даны своими уравнениями прямая l и плоскость :


Определим точку пересечения прямой с плоскостью. Перейдем к параметрическому виду задания прямойl:
 ,
,
 ,
,
 (6.30.)
(6.30.)
Найдем значение
t соответствующее точке пересечения
прямой и плоскости. Так как по условию
прямая пересекает плоскость, то

(6.30.) подставим в уравнение плоскости, найдем параметр t для точки пересечения по формуле:
 .
.
Подставив t в каждое из уравнений (6.30.) получим координаты искомой точки.
Пример 6.4.1.
Найти точку пересечения прямой
 с плоскостью
с плоскостью
 .
.
Решение: Перейдем от канонического задания прямой к параметрической форме; подставим x,y,z в уравнение плоскости и найдем t:
 ,
,  ,
,  ,
,  .
.
Подставим t в параметрическое уравнение:
 .
.
Ответ: M(16;37;34).
6.4.2.Условие параллельности и перпендикулярности прямой и
плоскости
Пусть в R3даны прямая l и плоскость :



Выясним условия параллельности и перппендикулярности прямой и плоскости, опираясь на взаимное расположение вектора нормали и направляющего вектора прямой.
Если прямая
и плоскость параллельны (см. Рис.6.11.),
то


В координатной
форме:
 (6.31.)
(6.31.)
Если прямая l
и плоскость
перпендикулярны (см.Рис.6.12.), то
 коллинеарные
коллинеарные
 (6.32.)
(6.32.)
Условия (6.31.) и (6.32.) называются соответственно условиями параллельности и перпендикулярности прямой и плоскости.
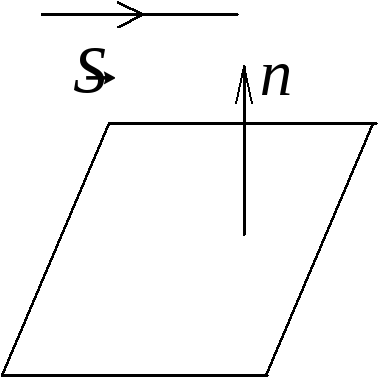

Рис.6.11. Рис.6.12.
Пример 6.4.2.
Доказать, что прямая

и плоскость
 параллельны.
параллельны.
Решение: Найдем
направляющий вектор прямой:

нормальный вектор плоскости имеет координаты:

Проверим условие
(6.31.)
 .
.
Ответ: Прямая и плоскость параллельны.
6.4.3.Угол между прямой и плоскостью
Под углом между
прямой и плоскостью понимается любой
из двух смежных углов, образованных
прямой и ее проекцией на плоскость
(Рис.6.13.). Обозначим один из углов между
прямой и ее проекцией через .
А угол между нормальным вектором
 и
направляющим вектором прямой
и
направляющим вектором прямой
 через
:
через
:
 ,
,

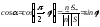

Рис.6.13.
В координатной
форме:
 ,
, 
 (6.33)
(6.33)
Контрольные вопросы и задания.
-
Как найти точку пересечения прямой с плоскостью?
-
Что понимают под углом между прямой и плоскостью?
-
Назовите условия перпендикулярности и параллельности прямой и плоскости.
-
Как найти проекцию точки на плоскость?
-
Записать уравнение плоскости, проходящей через две данные точки параллельно данной прямой.
Задачи для самостоятельной работы.
1. Записать уравнение плоскости, проходящей через данную точку параллельно двум данным прямым.
2. Написать уравнение плоскости, проходящей через начало системы координат и линию пересечения плоскостей 2x+5y-6z+4=0 и 3y+2z+6=0.
3. Определить величину угла между прямой (x+3)/1=(y-2)/(-2)=(z+1)/2 и плоскостью 4x+2y+2z-5=0.
4. Найти точку пересечения прямой и плоскости:
5. Доказать, что прямые x=2+4t, y=-6t, z=-1-8t и x=7-6t, y=2+9t, z=12t лежат в одной плоскости, и написать уравнение этой плоскости.
-
Найти проекцию точки A(1,2,-3) на плоскость 6x-y+3z-41=0.
-
Найти точку симметричную точке A(2,7,1) относительно плоскости x-4y+z+7=0.