5. Вектора в трёхмерном пространстве .

5.1. Угол между двумя векторами. Проекция вектора на ось.

Определение 5.1.1.

Углом между векторами называется наименьший угол

j(0 Јj<p), на который надо повернуть один из векторов до его совпадения со вторым .

Определение 5.1.2.

Под углом между вектором и осью l понимают угол j между векторами и единичным вектором этой оси .

Теорема 5.1.1.

Проекция вектора на ось l равна модулю вектора 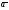, умноженному на косинус угла j между вектором и осью .

пр = ппcosj

Доказательство: Рассмотрим треугольник OBB₁ : BB₁ OB₁

Рис.5.1.

Проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций этих векторов на ту же ось.

Определение 5.1.3.

Произведение проекции вектора на ось и единичного вектора этой оси называется составляющей вектора по оси l (см.Рис.5.2.).

_Состl =пр_l=

Рис.5.2.

5.2. Координаты вектора заданного двумя точками.

Пусть в пространстве R³ дан вектор , т. A(x₁;y_1;z₁), т.B(x₂;y₂;z₂).

Введём в рассмотрение

Очевидно , что

Рис.5.3.

Вектора и в разложении по базису:

Чтобы найти координаты вектора, заданного двумя точками, нужно из соответствующей координаты конца вектора вычесть соответствующую координату начала данного вектора.

5.3.Условие коллинеарности двух векторов в координатной форме

Пусть векторы и заданы в координатной форме:

где - некоторое число, если , тогда при умножении вектора на число его координаты также умножаются на это число .

Следовательно (5.2)

Для того чтобы два вектора были коллинеарны необходимо и достаточно чтобы их одноименные координаты были пропорциональны.

5.4. Скалярное произведение векторов в координатной форме

_{Пусть даны в R}³ вектора и 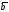, умножим

_{Раскроем скобки применив распределительный закон умножения. Рассмотрим произведение орт:}

т.к. они перпендикулярны

в результате упрощений получим:

Скалярное произведение двух векторов равно сумме произведений их одноимённых координат.

Условия перпендикулярности двух векторов.

Для того, чтобы два вектора были взаимно перпендикулярны, необходимо и достаточно чтобы сумма произведений их одноимённых координат была равна нулю: x₁x₂+y₁y₂+z₁z₂=0

5.5. Определение длины вектора и угла между двумя векторами.

Поскольку то _(5.4.)

Пусть

_(5.5.)

Модуль вектора равен квадратному корню из суммы квадратов его координат .

Если вектор задан координатами т.A и т.B _{, то модуль его равен:}

_(5.6.)

Заметим, что длина вектора равна расстоянию между т. A и т. B.

Пусть даны ,

т.к.

(5.7.)

Пример 5.5.1. Определите модуль вектора ?

Решение: Применим формулу (5.5.)

Пример 5.5.2.

Определить длину вектора если

- угол между векторами и

Решение: применим формулу (5.4.)

Пример 5.5.3.

Определить угол В треугольника АВС с вершинами

Решение:

Построим треугольник ABC (см. Рис.5.4.) и векторы и ,

Рис.5.4.

Найдем координаты векторов и по формуле (5.1.)

, найдем по формуле (5.3.)

Применим формулу (5.7.):

Ответ:

Пример 5.5.4. Даны три силы Найти величину равнодействующей силы R и работу, которую она производит, когда точка M₁(0,1,0) ее приложения, двигаясь прямолинейно, перемещается в положение M₂(1,0,1).

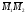Решение: Найдем равнодействующую сил , найдем ее величину . Искомая работа или , найдем координаты по формуле (5.1.) ={1;-1;1} и по формуле (5.3.): A=201+9(-1)+121=23 .