Индивидуальные задания и последовательность выполнения работы

Перенесите данные своего варианта в электронную таблицу и проведите интерполирование в соответствии с заданием. Постройте график функции, нанесите на него точку интерполирования, оцените погрешность интерполирования, сохраните работу в своей папке и покажите преподавателю.

Задания для проведения интерполяции. Таблица 3

№ варианта	Y	X	Тип интерполяции
1	2 4 3 1	1 2 3 4	линейная при Х=2,25
2	4 3 3.5 3.2	1 2 3 4	линейная при Х=3,7
3	27 32 56 100	18 20 22 24	линейная при Х=23,15
4	1 3 4 2	7 8 9 10	Квадратичная при Х= 5,5
5	2.7 5.4 3 -1	1 2 3 4	Квадратичная при Х= 1,5
6	-1 -0.87 -0.25 0	-1 -2 -3 -4	Квадратичная при Х= -3,6
7	-1 -0.87 -0.25 0	4 3 2 1	линейная при Х=1,15
8	34 28 56 4	34 38 42 46	линейная при Х=39,5
9	4 56 28 34	34 38 42 46	Квадратичная при Х= 36
10	1 3 5 7	4 5 6 7	линейная при Х=5,5
11	4 5 6 7	1 2 3 4	линейная при Х=2,25
12	1.2 4.8 4.7 4.7	4 5.6 6.2 8	Квадратичная при Х= 7
13	34 38 42 46	-1 -0.87 -0.25 0	Квадратичная при Х= -0,7
14	1.75 33.4 22.4 17.2	1.55 2.55 4.55 10	Квадратичная при Х= -0,7
15	3 10 50 200	10 20 30 40	линейная при Х=2,25

Лабораторная работа №4 (2ч.) РЕШЕНИЕ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ПОМОЩЬЮ ПЭВМ.

Цель работы: изучение численных методов решения нелинейных алгебраических уравнений.

Теория вопроса

Уравнение f(x)=0, левая часть которого представляет собой многочлен от х, степени больше единицы или содержит тригонометрические, логарифмические и другие элементарные функции называется нелинейным. Например,

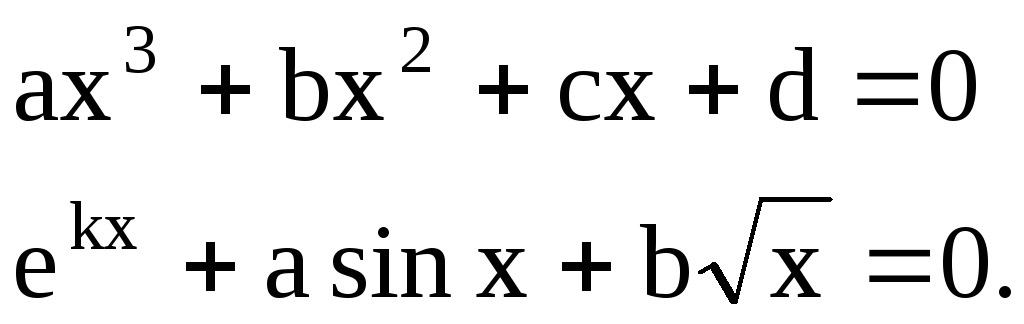
Значения х, удовлетворяющие условию f(x)=0, называются корнями этого уравнения. Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют получить корень уравнения по некоторым конечным аналитическим формулам. Однако, такие формулы в общем случае известны только для небольшого класса нелинейных уравнений.

Наиболее простым и наглядным методом решения уравнений является графический, но его можно использовать только в том случае, когда возможно построить график функции на плоскости.

Пример 1. Решить уравнение tgx=ax (a,x>0). Обозначим y₁=tgx, y₂=ax. Построим на плоскости графики функций y₁ и y₂ и отметим, что точки, в которых y₁=y₂ и будут решением (или решениями) исходного уравнения. То есть, те значения переменной х, при которых y₁=y₂ обращают исходное уравнение в тождество и являются его корнями.

Так как функция tgx периодическая, то существует бесконечное множество тангенсоид, из которых на графике показаны только три. Причем, при и т.д., . Сказанное означает, что прямая y₂=ах будет пересекать тангенсоиды бесконечное число раз, и, следовательно, исходное уравнение имеет бесконечное множество корней.

В этом примере использование графического метода сразу позволяет сделать заключение о множественности корней исходного трансцендентного уравнения. Достоинством графического метода является его наглядность, а недостатками низкая точность решения и ограниченность количества переменных.

Н айти корни уравнения можно и численными методами.

Итерационными (численными) называются методы последовательного приближения к корню уравнения. Сущность этих методов состоит в следующем. Задается точность решения е. Затем поиск корня происходит в два этапа. На первом этапе выполняется отделение корней, т.е. определяются отрезки [a,b]. На каждом из которых функция f(x) непрерывна и имеет только один корень. По сути дела, на этом этапе находят приближенные значения корней с погрешностью, задаваемой длиной отрезка [a,b]. На втором этапе с помощью некоторого алгоритма происходит последовательное уточнение значения корня до нахождения такого приближенного значения х истинной величины корня Х^*, при котором выполняется условие

Каждое повторное уточнение корня называется итерацией. Число итераций заранее неизвестно и зависит от требуемой точности решения е.

Отделение корней может быть выполнено следующим образом. Вычисляется с некоторым шагом h (предположительно меньшим расстояния между корнями) ряд значений функции f(x) в интересующей нас области изменения х. Если функция f(x) непрерывна, то корни уравнения будут расположены между теми соседними координатами х, в которых функция имеет разные знаки (в частном случае одно из этих значений функции может равняться нулю) и для которых, следовательно, выполняется соотношение f(x)*f(x+h)0.

Пример 1. Отделить корень уравнения (х-1)²-е^-х=0 в области [-5,5].

Просчитываем с помощью ЭТ значения функции от х_а= -5 до х_b=5 с шагом h=5 и получаем: корень уравнения расположен между х = -3,0 и х = -2,5.

Если функция f(x) на отрезке [a,b] непрерывна, то уточнение корня на отрезке [a,b] до величины, удовлетворяющей одному из условий обычно осуществляется одним из следующих итерационных методов: деления отрезка пополам (МДО); хорд (МХР); касательных (МК). Рассмотрим МДО.

В методе деления отрезка пополам отрезок [a,b] делим пополам и вычисляем с=(а+b)/2 и значение f (c). Если выполняется соотношение , где р – погрешность вычисления функции (например, р=0001), то с является корнем уравнения. В противном случае выбираем тот из отрезков [a,с] или [с,b], на концах которого функция f(x) имеет разные знаки. Выбранный отрезок снова обозначим через [a,b] и опять делим пополам и т.д. Процесс повторяется до тех пор, пока не будет получено точное значение корня или длина b-а очередного отрезка [a,b] не станет меньше заданной точности е. Вышеизложенное реализуется следующим алгоритмом (рис. 5). Учтите, что в алгоритме отсутствует проверка на правильность ввода границ первоначального интервала.

Преимуществом МДО является возможность его применения к любым непрерывным функциям и простота выполнения вычисленного процесса, недостатком – низкая скорость приближения к корню.