Исходные данные к выполнению работы Таблица 1

№ п/п	приближ число А	приближ число В	приближ число С	приближ число D
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	5,3714 493,14 37,541 837,54 21,692 9,7483 748,97 54,371 378,45 15,341 1,1236 874,36 28,536 475,16 14,937 478,65	0,2974 47,13 9,275 17,31 5,183 0,3792 72,16 7,259 37,11 2,756 0,7256 54,62 4,529 82,25 4,572 0,6527	47,3257836 3,57896218 0,76588764 5492,35428 23,7652328 4,35869257 0,24753682 2954,43529 76,2353264 2,83562932 0,86357248 4354,59263 32,5237657 9,26536723 0,42753867 0,56389421	9216,54716 713,219623 54,56,7215 716759,316 6219,57472 317,296125 21,5654718 957167,397 6192,74745 961,317297 74,5621364 376157,942 4772,91653 172,316925 15,7546243 52,6238496

Контрольные вопросы

1. Какие виды погрешностей Вы знаете?

2. Что такое относительная погрешность? Абсолютная погрешность?

3. Что принимается за погрешность приближенного числа, если не указаны границы погрешности?

4. Какие цифры в приближенном числе называются значащими?

5. Что такое нормализованная форма представления приближенного числа?

6. Может ли быть результат выполнения арифметических операций с приближенными числами точным числом?

7. Как определяется погрешность функции?

8. Какие правила учета погрешностей используют при массовых вычислениях?

9. Что такое погрешности ограничения?

10. Чем обусловлены погрешности округления при использовании ЭВМ?

Табулирование функций

Используя Excel провести табулирование функций:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. .

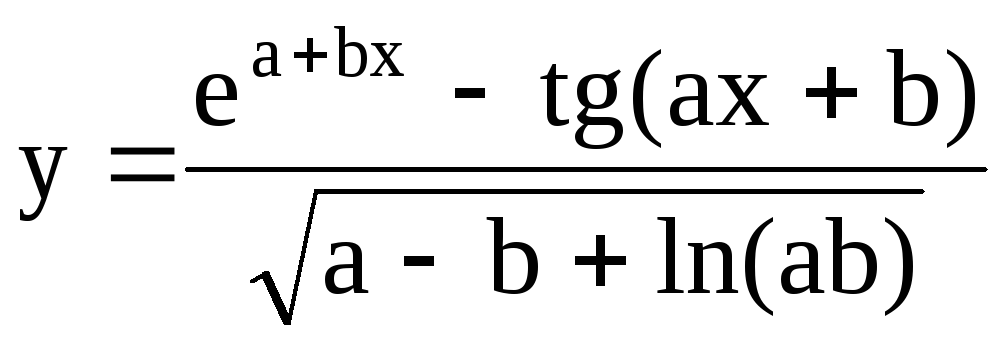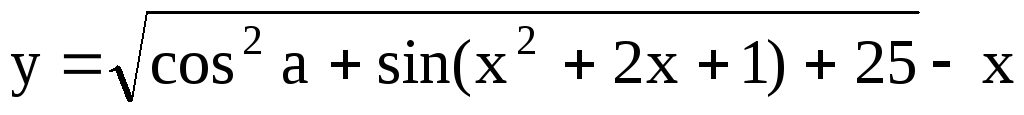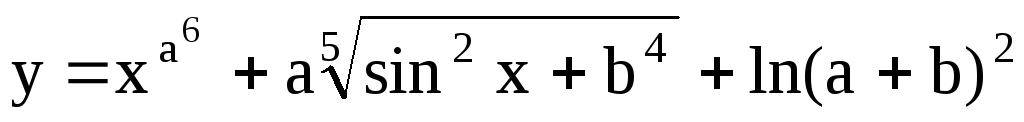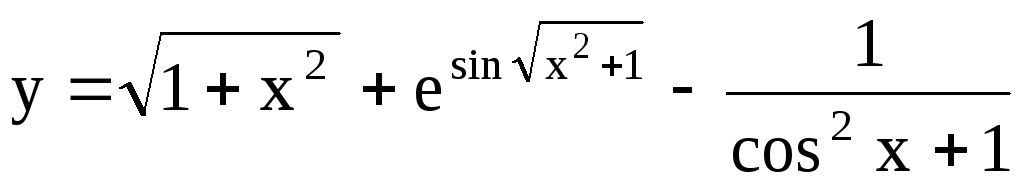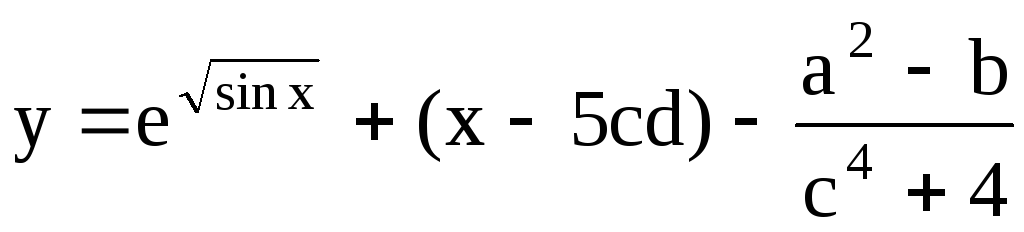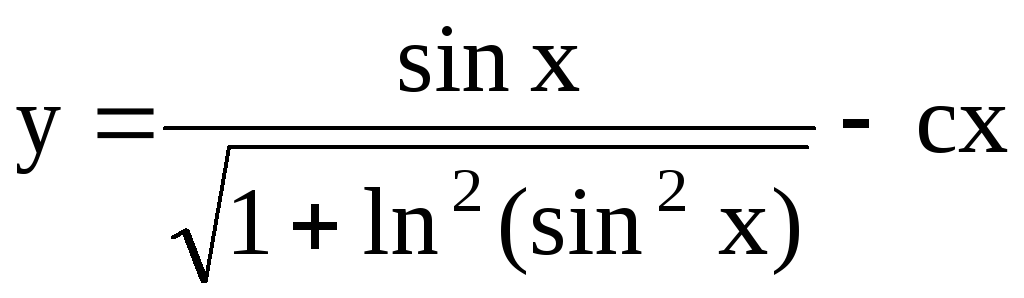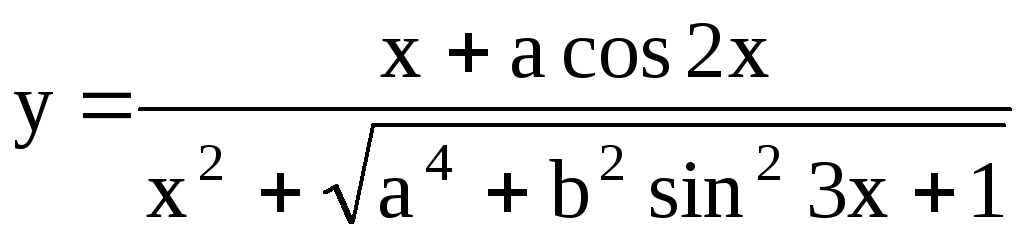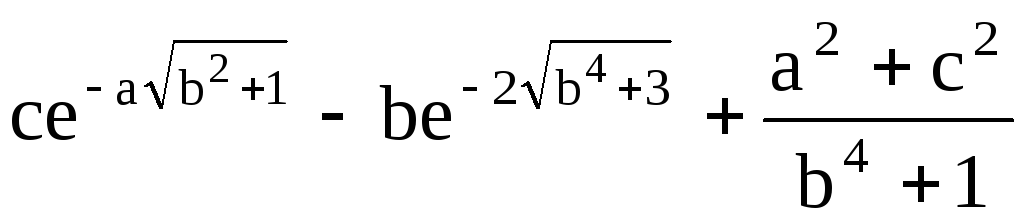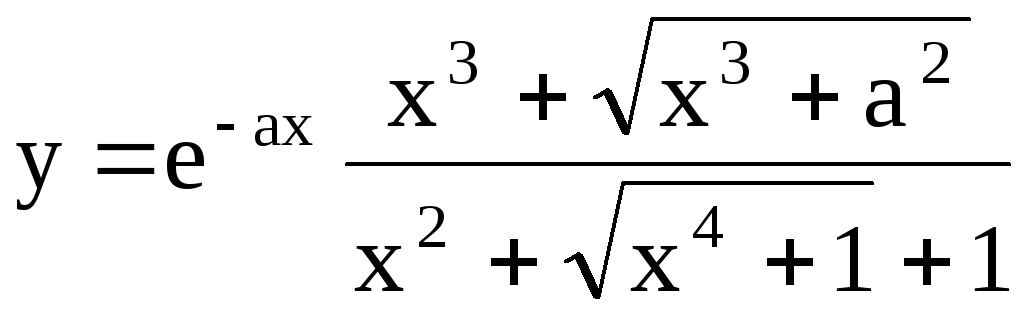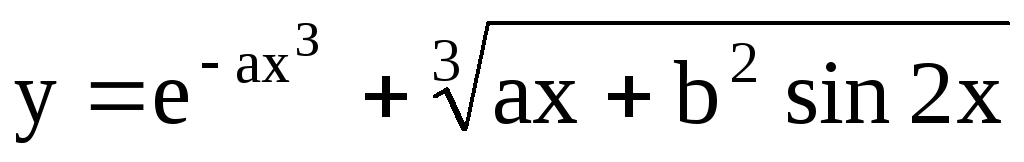При табулировании принять: а=0,1; b=0,05; с=8; d=100.

Табулирование провести на отрезке х[0,10]. Шаг табулирования выбрать самостоятельно. По результатам табулирования построить диаграмму в MS Excel.

Определить, есть ли на отрезке табулирования нули табулируемой функции. Результаты работы сохранить в своей рабочей папке и показать преподавателю.

Пример выполнения табулирования представлен на рисунке 1.

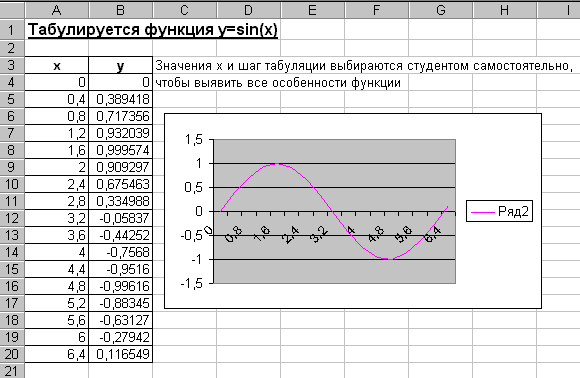
Рис. 1 Пример табулирования функции.

Лабораторная работа № 2. (2ч.) ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

Цель работы: ознакомить студентов с методами численного решения систем линейных алгебраических уравнений.

Теория вопроса

К решению систем линейных алгебраических уравнений (СЛАУ) сводятся многие задачи анализа и синтеза систем различной природы: механических, электрических, экономических и т.п.

В общем виде система n линейных алгебраических уравнений с n неизвестными записывается так:

а₁₁*х₁+а₁₂*х₂+ …+а_1n*x_n=b₁;

а₂₁*х₁+а₂₂*х₂+ …+а_2n*x_n=b₂;

………………………………

а_n1*х₁+а_n2*х₂+ …+а_nn*x_n=b_n;

где х₁,х₂,…,х_n – неизвестные системы;

а₁₁, а₂₁,…, а_nn – коэффициенты при неизвестных системы;

b₁,b₂,…,b_n - свободные члены системы.

В векторно-матричной форме СЛАУ можно записать

А*х=b,

где

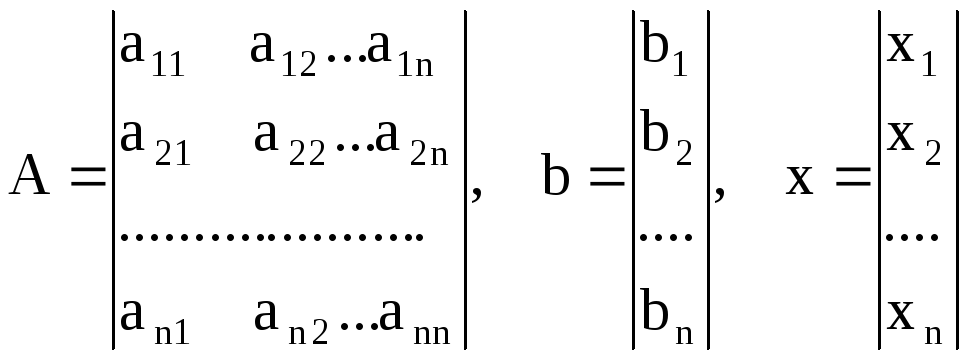
есть соответственно матрица коэффициентов, вектор-столбец свободных членов и вектор-столбец неизвестных.

Решением СЛАУ называется любая совокупность чисел а₁,а₂,…,а_n, которая, будучи подставленной на место неизвестных х₁,х₂,…,х_n в уравнения данной системы, обращает все эти уравнения в тождества.

Применяемые в практике численные методы решения СЛАУ делятся на две группы: точные (прямые) и приближенные (итерационные). Точными называются методы, которые в предположении, что вычисления ведутся без округления, позволяют получить точное решение за конечное число арифметических операций. Приближенные методы даже в предположении, что вычисления ведутся без округления, дают решение системы лишь с заданной точностью.

Прямые методы используются при решении на ЭВМ систем небольшого порядка (n<10³). Итерационные методы выгодно применять для систем высокого порядка (n10³-10⁶) со слабо заполненной матрицей коэффициентов.

На практике наиболее широко из прямых методов для решения СЛАУ используется метод Гаусса. Суть метода состоит в приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается х₁ из всех последующих уравнений системы. Затем, с помощью второго уравнения исключается х₂ из третьего и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным х_n, т.е. матрица системы будет приведена к треугольному виду. Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное неизвестное х_n. Далее, используя это значение из предыдущего уравнения вычисляем х_n-₁ и т.д. Последним найдем х₁ из первого уравнения.

Рассмотрим применение метода Гаусса для системы

а₁₁*х₁+а₁₂*х₂+ а₁₃*x₃=b₁;

а₂₁*х₁+а₂₂*х₂+а₂₃*x₃=b₂;

а₃₁*х₁+а₃₂*х₂+а₃₃*x₃=b₃.

Для исключения х₁ из второго уравнения прибавим к нему первое, умноженное на –а₂₁/а₁₁. Затем, умножив первое уравнение на –а₃₁/а₁₁ и прибавив результат к третьему уравнению, также исключим из него x₁. Получим равносильную систему уравнения вида:

а₁₁*х₁+а₁₂*х₂+ а₁₃*x₃=b₁;

а'₂₂*х₂+а'₂₃*x₃=b'₂;

а'₃₂*х₂+а'₃₃*x₃=b'₃.

Теперь из третьего уравнения полученной системы нужно исключить х₂. Для этого умножим второе уравнение на –а'₃₂/a'₂₂ и прибавим результат к третьему. Получим

а₁₁*х₁+а₁₂*х₂+ а₁₃*x₃=b₁;

а'₂₂*х₂+а'₂₃*x₃=b'₂;

а''₃₃*x₃=b''₃.

Таким образом, матрица СЛАУ имеет треугольный вид. На этом заканчивается прямой ход метода Гаусса.

Заметим, что в процессе исключения неизвестных приходится выполнять операции деления на коэффициенты а₁₁, а'₂₂ и т.д. Поэтому они должны быть отличными от нуля, в противном случае необходимо соответственным образом переставить уравнения системы. Обратный ход начинается с решения третьего уравнения системы:

x₃=b"₃/a"₃₃.

Используя это значение, можно найти х₂ из второго уравнения, а затем х₁ из первого:

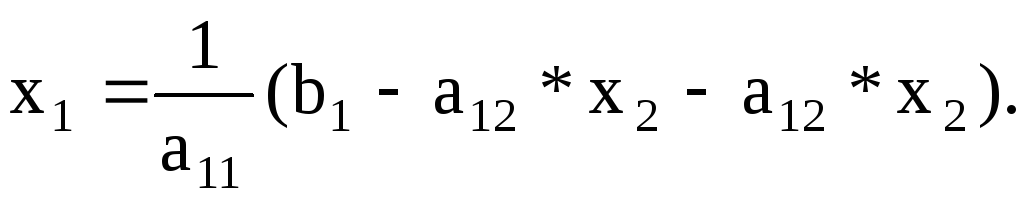
Аналогично строится вычислительный алгоритм для СЛАУ с произвольным числом уравнений.

Одним из самых распространенных итерационных методов решения СЛАУ, отличающийся простотой и легкостью программирования, является метод Гаусса-Зейделя. Проиллюстрируем этот метод на примере решения той же СЛАУ. Предположим, что диагональные элементы а₁₁, а₂₂, а₃₃ отличные от нуля (в противном случае можно переставить уравнения). Выразим неизвестные х₁, х₂ и х₃ соответственно из первого, второго и третьего уравнения системы:

Зададим некоторые начальные (нулевые) приближения значений неизвестных: х₁=х₁⁽⁰⁾, х₂=х₂⁽⁰⁾, х₃=х₃⁽⁰⁾. Подставляя эти значения в правую часть предыдущих выражений, получаем новое (первое) приближение для х₁:

х₁⁽¹⁾ = (b₁ - a₁₂^* х₂⁽⁰⁾ –a₁₃ *х₃⁽⁰⁾)/a₁₁.

Используя это значение для х₁ и приближение х₃⁽⁰⁾ для х₃, находим новое приближение для х₂:

х₂⁽¹⁾ = (b₂ – a₂₁^* х₁⁽¹⁾ –a₂₃ *х₃⁽⁰⁾)/a₂₂.

И наконец, используя вычисленные значения х₁=х₁⁽¹⁾, х₂=х₂⁽¹⁾, находим первое приближение для х₃:

х₃⁽¹⁾ = (b₃ – a₃₁^* х₁⁽¹⁾ –a₃₂ *х₂⁽¹⁾)/a₃₃.

Далее итерационный процесс продолжается по рекуррентным формулам:

х₁^(k) = (b₁ - a₁₂^* х₂^(k-1) –a₁₃ *х₃^(k-1))/a₁₁;

х₂^(k) = (b₂ – a₂₁^* х₁^(k-1) –a₂₃ *х₃^(k-1))/a₂₂;

х₃^(k) = (b₃ – a₃₁^* х₁^(k-1) –a₃₃ *х₂^(k-1))/a₃₃.