Теория вопроса

На практике известны три способа задания функций: аналитический, графический, табличный. В практике вычислений на ЭВМ использование графического способа задания функций практически невозможно, а аналитического иногда затруднительно, вследствие громоздкости зависимости y=f(x) (например, она содержит трудно вычисляемые выражения, сложные интегралы, дифференциалы и т.п.). Поэтому в данных случаях, с точки зрения экономии времени и средств, приходят к необходимости использования табличных данных для приближенного вычисления функции y при любом значении (из некоторой области) переменной x.

Этой цели и служит задача о приближении (аппроксимации) функций: данную функцию f(x) требуется заменить (аппроксимировать) некоторой функцией (x) так, чтобы отклонение (x) от f(x) в заданной области было наименьшим. Функция (x) при этом называется аппроксимирующей.

Если приближение строится на заданном дискретном множестве точек x_i, то аппроксимация называется точечной. При построении приближения на непрерывном множестве точек (например, на отрезке) аппроксимация называется непрерывной или интегральной.

Одним из основных типов точечной аппроксимации является интерполирование. Интерполяцию в свою очередь делят на кусочную (или локальную) и глобальную. Если интерполирование проводится для отдельных участков рассматриваемого интервала изменения x, то в этом случае имеют кусочную интерполяцию. Если интерполирование проводится для всего интервала изменения x, то говорят о глобальной интерполяции.

Как правило, интерполяция используется для аппроксимации функции в промежуточных точках между крайними узлами интерполяции. Однако, иногда она используется и для приближенного вычисления функции вне рассматриваемого отрезка, заключенного между крайними точками. Такое приближение называется экстраполяцией.

Простейшим и часто используемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные соседние точки соединяются прямолинейными отрезками, и функция заменяется ломаной с вершинами в данных точках. Уравнения e = a*x + b каждого отрезка ломаной в общем случае разные. Следовательно, при использовании линейной интерполяции сначала нужно определить отрезок, на который попадает значение аргумента x, а затем подставить его в соответствующее уравнение для вычисления y и найти приближенное значение функции в этой точке.

Геометрические пояснения линейной интерполяции и параметров уравнения a и b приведена на рис. 3.

Локальная квадратичная интерполяция проводится аналогично, но по трем точкам на отрезке [x(i-1),x(i+1)]. В качестве интерполяционной функции в данном случае на каждом из отрезков принимается квадратичный трехчлен y = a*x²+b*x+с. Такую интерполяцию еще называют параболической, так как уравнение квадратного трехчлена содержит три неизвестных коэффициента a, b, c для определения которых необходимо решать систему трех уравнений. Указанная система записывается исходя из условия прохождения параболы через три точки (x(i+1),y(i-1)), (x_i,y_i), (x(i+1),y(i+1)).

Тогда эту систему уравнений можно записать в следующем виде:

a*x(i-1)²+b* x(i-1)+c= y(i-1)

a*x_i²+b*x_i+c= y_i

a*x(i+1)²+b* x(i+1)+c= y(i+1).

Как видим, при интерполяции основным условием является прохождение графика аппроксимирующей функции через данные значения функции в узлах интерполяции.

Пример 1. Определить значение функции Y, заданной таблично в точке Х=0,5

Y	X
2 3 1 -4	0 1 2 3

Так как в таблице отсутствуют значения функции в точке Х=0,5, то необходимо провести интерполяцию. Будем проводить линейную интерполяцию на отрезке, включающем точку Х=0,5. Очевидно, что это отрезок [0,1] в таблице значений функций.

Так как значения функции на концах интервала известны, то при линейной интерполяции можно записать систему линейных алгебраических уравнений, из которой определяются коэффициенты a и b линейной интерполяционной формулы

Y=a+bx

2=a+b*0

3= a+b*1 а=2; b=1

Система легко решается. Тогда, значение функции в точке Х=0,5 можно определить как

Y=2+1*0,5=2,5

Теперь проведем квадратичную интерполяцию для той же функции в той же точке Х=0,5. Для этого запишем систему уравнений для трех узлов, чтобы определить коэффициенты a, b и с в интерполяционной формуле Y=a+bx+cx²

2=a+b*0+c*0²

3=a+b*1+c*1²

1=a+b*2+c*2²

Преобразуем систему

а=2

b+c=1

2b+4c=-1

Система легко решается, но если уравнения более сложные, то лучше использовать любой (например, матричный) метод ее решения.

Из системы уравнений находим

Значение функции в точке Х=0,5 при такой интерполяции будет равно

Как видим, результат квадратичной интерполяции отличается от результата линейной интерполяции.

Если построить график табличной функции, то можно увидеть, что она нелинейна на отрезке [0,2]. Поэтому квадратичную интерполяцию можно считать более точной. Относительная погрешность линейной интерполяции по отношению к квадратичной составит

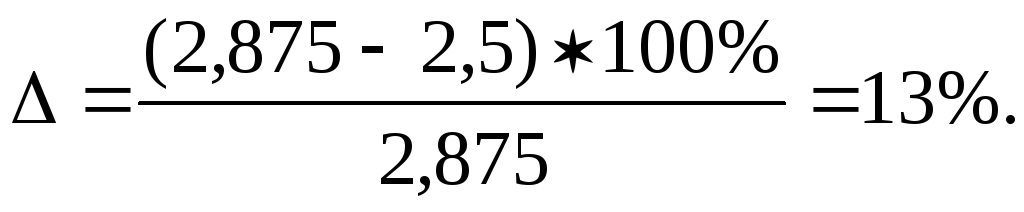
Если эта погрешность меньше, чем требуемая точность интерполяции на заданном отрезке, то можно использовать и линейную интерполяцию, Аналогично проводятся интерполяции и более высоких порядков (кубическая, биквадратная и т.д.).