Индивидуальные задания и последовательность выполнения работы

Методом трапеций по своему варианту вычислить определенные интегралы от функций, приведенных в таблице исходных данных. В качестве рабочего инструмента использовать VB или MS Excel.

Исходные данные к выполнению работы Таблица 5

N/B	Функция	a	b	N/B	Функция	a	b
1	2sin(x)dx	0	/2	13	5sin(x)dx	/2	
2	4xdx	2	4	14	3x2dx	1	2
3	4x3dx	1	2	15	x2dx	1	3
4	3cos(x)dx	0	/2	16	5cos(x)dx	/2	
5	2x3dx	0	2	17	4sin(x)dx	0	/2
6	4cos(x)dx	/2		18	2xdx	2	4
7	x3dx	0	1	19	6x2dx	0	2
8	3sin(x)dx	0	/2	20	2cos(x)dx	/2	
9	4sin(x)dx	/2		21	2x5dx	1	4
10	9x2dx	1	2	22	3cos(x)dx	/2	
11	4cos(x)dx	0	/2	23	3sin(x)dx	/2	
12	6xdx	2	3	24	2xdx	2	4

Контрольные вопросы:

1. Назовите сущность и отличия известных Вам методов численного интегрирования.

2. Поясните геометрический смысл вычисления определенного интеграла.

3. Расскажите сущности и поясните алгоритм вычисления определенного интеграла методами прямоугольников, трапеций, Симпсона.

4. Как оценить точность вычисления определенного интеграла.

Лабораторная работа № 6. (2ч.) ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫЧНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА НА ПЭВМ.

Цель работы: ознакомить студентов с численными методами решения дифференциальных уравнений на ПЭВМ.

Теория вопроса

Обыкновенным дифференциальным уравнением 1-го порядка называется уравнение, содержащее неизвестную функцию одного аргумента и ее производную

dy/dx=f(x,y) или y'=f(x,y).

Решением дифференциального уравнения является неизвестная функция

y=f(x,C).

Cодержащийся в решении свободный член С может принимать различные значения, поэтому на координатной плоскости решение представляется в виде семейства кривых. Например, решением дифференциального уравнения dy/dx=y или y'= y является зависимость y=Се^х. При различных значениях коэффициeнта С получаем семейство кривых, каждая из которых удовлетворяет исходному уравнению y'= y (см. рис.1). Для того, чтобы из множества кривых выявить одну, необходимо в дополнение к дифференциальному уравнению указать начальные условия – координаты точки, через которую эта кривая должна проходить.

Например, если нам нужно, чтобы решение уравнения y'= y проходило через точку х=0, y=2, что обычно записывается в виде y(0)=2, то через точку L с координатами (0;2) будет проходить только одна кривая y=2е^х. Если задаться начальными условиями y(0)=1, то через точку Р(0;1) будет проходить кривая решения дифференциального уравнения y=1е^х.

Для решения дифференциального уравнения численными методами его приводят к виду y'= f(x,y). Такая форма представления дифференциального уравнения позволяет для любой точки координатной плоскости вычислить производную, которая представляет собой тангенс угла наклона касательной к проходящей через эту точку кривой y= f(x).

На рис. 8 показаны три касательные к функции y=2е^х в точках К(-0,5;1,2), L(0;2), M(0,5;3,3) и три касательные к функции y=1е^х в точках N(-0,5;0,6), P(0;1), Q(0,5;1,65). Если опустить из этих точек перпендикуляр на ось 0х, то получим обладающие интересным свойством прямоугольные треугольники, ограниченные перпендикулярами, осью 0х и касательными. В любом из треугольников длина катета, лежащего на оси 0х, равна 1. Длина другого катета равна ординате точки, к которой проведена касательная, поэтому тангенс угла наклона каждой из касательных численно равен ординате точки, из которой проведена касательная в соответствии с исходным дифференциальным уравнением y'=y.

С делаем небольшое обобщение. Для кривой y=2е^х касательные, проведенные в точках К,L,M и любых других точках этой кривой, будут иметь тангенс угла наклона, равный ординате точки в полном соответствии с дифференциальным уравнением y'=y. То же самое можно отметить и для кривой y=1е^х. Обе кривые представляют собой решения дифференциального уравнения y'=y с разными начальными условиями.

Таким образом, под решением дифференциального уравнения подразумевается походящая через заданное начальное условие кривая y= f(x), касательная в любой точке этой кривой будет иметь тангенс угла наклона, определяемый исходным дифференциальным уравнением.

Рассмотрим некоторые методы численного решения дифференциальных уравнений.

1. Метод Эйлера. Дифференциальное уравнение вида y'= f(x,y) позволяет определить тангенс угла наклона касательной в любой точке искомой кривой y= f(x). Поэтому можно вычислить наклон касательной к кривой решения дифференциального уравнения в точке А(х_i,y_i), подставив ее координаты в правую часть дифференциального уравнения f(x₁,y₁) и затем продвинуться вдоль касательной на некоторое малое расстояние – шаг (рис. 9). Если шаг вдоль оси абсцисс обозначить h (рис. 9а), то мы придем в точку В с координатами x_i+1=x_i+h, y_i+1=y_i+h*tg ()=y_i+k₁.

Поскольку мы двигались вдоль касательной, а не кривой y=f(x), то разность ординат точек В и В' определяет погрешность метода (рис.9). Поэтому в методе Эйлера точку В называют приближенным решением дифференциального уравнения. Точка В' находится на кривой истинного решения дифференциального уравнения y=f(x,c₁), но ординату этой точки мы вычислить не можем и используем точку В, расположенную на некоторой другой кривой y=f(x,c₂) из семейства кривых возможных решений исходного дифференциального уравнения.

Подставив координаты точки В в дифференциальное уравнение, вычислим тангенс угла наклона касательной в этой точке y'=f(x_i+1,y_i+1), продвинемся вдоль этой касательной вперед на величину шага h к следующей точке. Продолжая эту процедуру, мы получаем последовательность коротких отрезков – ступеней, которые являются приближенным решением дифференциального уравнения (рис. 9б).

Математический метод Эйлера реализуется рекуррентной формулой

y_i+1=y_i+h*f(x_i,y_i),

где y_i – значение функции при х=х_i;

y_i+1 – значение функции при х= x_i+h;

f(x_i,y_i) – численное значение функции при х=х_i и y= y_i;

h – величина шага.

Очевидно, что с уменьшением величины шага h погрешность вычисления уменьшается. Погрешность метода Эйлера пропорциональна h².

2. Метод Рунге-Кутта. Это наиболее точный и потому наиболее употребительный метод интегрирования дифференциальных уравнений, использующий не одну, а четыре точки, которые позволяют оценить изменение кривизны кривой истинного решения дифференциального уравнения на протяжении следующего шага. На рис. 10 дана геометрическая интерпретация метода Рунге-Кутта.

Как и в методе Эйлера, в каждой из четырех точек А₁, А₂, А₃, А₄, последовательно вычисляются тангенс угла наклона касательной, равный величине производной из дифференциального уравнения, который затем представляется в виде приращения ординаты на величину шага h – коэффициенты k₁, k₂, k₃, k₄. Поскольку в точках А₂ и А₃ учет изменения кривизны оказывает вдвое большее влияние на возможное изменение кривизны кривой истинного решения, ордината искомой точки В определяется как средневзвешенное коэффициентов k₁, k₂, k₃ и k₄ по формуле

y_i+1= y_i+( k₁+2 * k₂+2 * k₃ + k₄)/6,

где k₁= h* f(x_i,y_i),

k₂= h* f(x_i + h/2,y_i + k₁/2),

k₃= h* f(x_i + h/2,y_i + k₂/2),

k₄= h* f(x_i + h,y_i + k₃),

Последовательность вычислений по методу Рунге-Кутта следующая. В точке А₁(x_i,y_i) вычисляем тангенс угла наклона искомой кривой, который приравниваем к отношению k₁/h; из этого отношения определяем величину коэффициента k₁; используя его, продвигаемся вдоль касательной на половину шага вперед и вычисляем тангенс угла наклона в точке А₂= (x_i + h/2,y_i + k₁/2). Вычислив новый тангенс угла наклона в этой точке, определяем коэффициент k₂ и опять начинаем движение из точки А₁(x_i,y_i), идем на половину шага вперед и в точке А₃= (x_i + h/2, y_i + k₂/2) вычисляем тангенс угла наклона. Определяем величину коэффициента k₃, и опять начинаем из точки А₁(x_i,y_i), но делаем теперь полный шаг к точке А₄= (x_i + h, y_i + k₃), где вычисляем тангенс угла наклона и коэффициент k₄. Полученные коэффициенты усредняем по вышеприведенной формуле и делаем окончательный шаг из точки А₁(x_i,y_i) в точку В(x_i+1,y_i+1).

x_i+1 = x_i + hy_i+1 = y_i+( k₁+2* k₂+2* k₃+k₄)/6.

Далее последовательность вычисления координат следующей точки повторяется для n шагов, которая позволит получить табличную функцию – приближенное решение дифференциального уравнения.

Погрешность метода Рунге-Кутта весьма мала и составляет h⁴.

П ример 1. Пусть имеется дифференциальное уравнение

описывающее зависимость прибыли Р от доходов M и издержек N предприятия, причем и доходы и издержки являются функцией прибыли. Требуется определить изменение прибыли с течением времени. Издержки содержат как постоянную, так и переменную составляющие, поэтому (задавшись конкретным видом M(P) и N(P) исходное уравнение можно привести к виду:

В начальном периоде времени прибыль нулевая, поэтому начальное условие будет: P=0 при t=0.

Решим это уравнение с помощью метода Рунге-Кутта с помощью электронных таблиц.

Вычислим коэффициенты к_1, к_2, к_3, к₄ для нашего уравнения_.

k₁ =h*(b-P)*c; k₂=h*(b-(P+k₁/2))*c; k₃=h*(b-(P+k₂/2)*c; k₄=h*(b-(P+k₃))*c.

Тогда, значение прибыли в момент времени i+1 будет

P_i+1=P_i+( к_{1 +}2*к₂ +2*к₃+к₄)/6

Зная прибыль в момент времени t=0, можно найти ее в любой другой момент времени, выполняя шаги решения уравнения. Следует ожидать, что с течением времени прибыль выйдет на некоторую установившуюся величину. Ниже приведен фрагмент листа электронной таблицы с решение этого уравнения (Рис.11).

Р ис. 11. Решение дифференциального уравнения методом Рунге-Кутта.

В ячейках таблицы находятся следующие формулы:

A12) 0 ; B12) 0; C12) =B12+(D12+2*E12+2*F12+G12)/6; D12) =($B$7-B12)*$B$8/$B$6*$B$9; E12) =($B$7-B12-D12/2)*$B$8/$B$6*$B$9; F12) =($B$7-B12-E12/2)*$B$8/$B$6*$B$9; G12) =($B$7-B12-F12)*$B$8/$B$6*$B$9; A13) =A12+$B$9; B13) =C12.

или в привычной форме:

A12) t=0

B12) P=0

C12) P_i+1=P_i+( к_{1 +}2*к₂ +2*к₃+к₄)/6

D12) k₁ =h*(b-P)*c/a

E12) k₂=h*(b-(P+k₁/2))*c/a

F12) k₃=h*(b-(P+k₂/2)*c/a

G12) k₄=h*(b-(P+k₃))*c/a

A13) t_i+1=t_i+h

B13) P_i+1

Решение состоит в копировании блока ячеек C12:H12 и A13:B13 вниз, при этом будет рассчитываться прибыль по шагам и выполняться шаги по времени с приращением h. P_идеал – точное решение исходного уравнения (дано для сравнения с приближенным численным решением)

Решение дифференциального уравнения представлено на рис. 11.

Р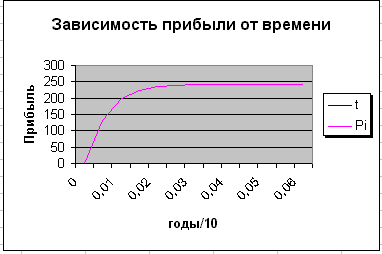 ис.12. Зависимость прибыли от времени.

На рисунке хорошо видно, что примерно через 5 месяца прибыль стабилизируется, а доходы и издержки придут в равновесие.