5. Графическое представление сгруппированных рядов данных натурных наблюдений

Для графического изображения рядов распределения стро­ится гистограмма . Резуль­таты расчетов сводим в таблицу 3.

Таблица 3

Определение ординат эмпирических кривых распределений

	Границы интервалов, мг/л		Частота, ni		Относительная частота, nотн		Приведенная частота, nпр
1		2		3		4		5
1		18,86 — 22,93		1		0,05		0,012
2		22,93 — 27,00		5		0,25		0,06
3		27,00 — 31,07		7		0,35		0,086
4		31,07 — 35,14		6		0,30		0,07
5		35,14 — 39,21		1		0,05		0,012

n_отн — относительная частота определяется отношением эмпирической частоты к объему выборки и характеризует вероят­ность появления случайной величины в каждом интервале.

n_пр — приведенная частота или плотность распределения случайной величины в заданном интервале:

Гистограмма

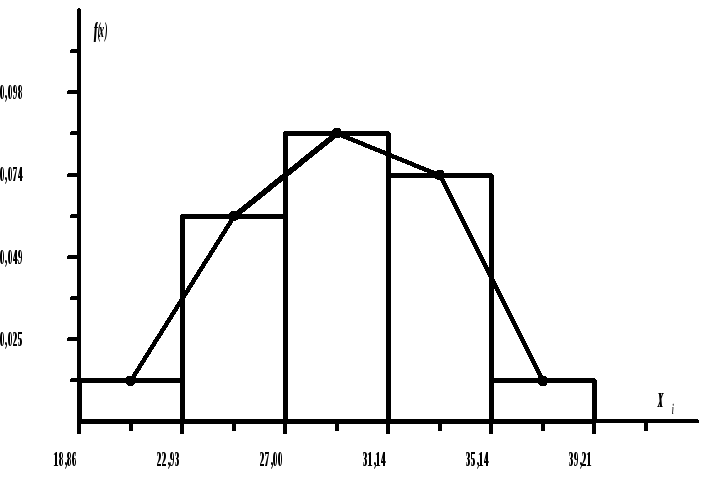
6. Проверка статистических гипотез:

а) проверка выборок на однородность;

Вопросы удлинения рядов данных натурных наблюдений преследует цель корректировки статистических параметров. Для проверки выборок в сходстве формирования случайных величин используют статистические критерии однородности. Как правило, анализируются выборки попарно. Результатом статистического анализа на однородность является объединение двух выборок в одну или отрицание однородности между сравниваемыми сово­купностями. В качестве примера использования статистических критериев однородности при практических расчетах студенты об­мениваются выборками и проверяют их на однородность. Для рас­четов используются критерии однородности: параметрический — критерий Фишера; непараметрический — критерий Вилкоксона.

Критерий Фишера основан на равенстве дисперсий выбо­рок распределенных приближено нормально. Расчетное значение критерия Фишера определяется по следующей формуле:

,

(23)

причем необходимо выполнение условия D_x > D_y, где

D_x — дисперсия выборки X (допустим, что выполняется вышеприведенное условие);

D_y — дисперсия выборки Y (по условию меньше дисперсии выборки X).

Для определения области допустимых значений необхо­димо задаться уровнем значимости и числом степеней свободы (для практических расчетов уровень значимости принимаем рав­ным 0,05, число степеней свободы рассчитывается по следующей зависимости:

).

Используя таблицы F-распределения (Приложение 2), оп­ределяется критическое значения критерия в зависимости от вы­бранного уровня значимости и числа степеней свободы. Если вы­полняется условие, при котором расчетное значение критерия Фи­шера не превосходит критическое, то можно предположить, что наши ряды однородны и сравниваемые выборки можно объединить в один ряд.

Из непараметрических критериев однородности можно выделить статистический критерий однородности Вилкоксона. Расчеты проводим в следующем виде и последовательности: зна­чения обеих выборок (X и Y) упорядочиваются вместе по величине, с учетом выборки из которой взято значение. Сумма инверсий оп­ределяется следующим образом: по построенному вариационному ряду из двух сравниваемых выборок проводят подсчет инверсий (инверсией считается величина, характеризующаяся следующим неравенством x_i > y_i) т. е. определяют, сколько значений Y-выборки находится перед каждым значением X-выборки. Расчетное значе­ние критерия Вилкоксона определяется по формуле:

.

(24)

Критическое значение статистического критерия однород­ности Вилкоксона определяется по таблицам или с помощью фор­мулы:

,

(25)

где коэффициент Z_ определяется по формуле:

2Ф0(Z)=1-,

(26)

где Ф_о — функция нормированного и центрированного закона нормального распределения (Приложение 1).

Допустим, необходимо сравнить две выборки на принад­лежность их одной генеральной совокупности:

№	1	2	3	4	5	6	7	8	9	10
Х	18,86	24,24	24,50	24,55	25,14	26,71	27,03	28,20	28,42	28,74
№	11	12	13	14	15	16	17	18	19	20
Х	28,87	30,02	31,03	31,19	31,91	32,91	33,49	34,06	34,27	39,21

	№	1		2	3		4	5	6	7	8		9	10
	Y	18.56		23.62	23.64		26.06	26.26	28.17	28.27	28.44		28.51	29.53
	№	11		12	13		14	15	16	17	18		19	20
	Y	34.78		34.84	35.52		35.59	36.66	37.03	37.77	38.02		38.43	42.85
Dx = 15,73						Dy = 32,77

Критерий Фишера:

.

Область допустимых значений определяется в зависимости от уровня значимости и числа степеней свободы:  = 0,05; m₁ = 19; m₂ = 19. По таблицам F-распределения (Приложение 2) опреде­ляем, что критическое значение критерия Фишера равно 2,15. По­лученное расчетное значение критерия Фишера не превышает кри­тического. Исходя из этого можно сделать вывод, что оно нахо­дится в области допустимых значений, и нулевая гипотеза под­тверждается, а это значит, что сравниваемые выборки однородны (принадлежат одной генеральной совокупности), и их можно объе­динить в одну. Данное предположение (о принадлежности сравни­ваемых выборок одной генеральной совокупности) проверим непа­раметрическим критерием однородности Вилкоксона. Для этого необходимо провести следующие действия:

1) Величины обеих выборок располагаются в порядке воз­растания с учетом того из какой выборки взято значение. Исполь­зуя рассматриваемый пример получим:

18,56(y);18,86(х);23,62(y);23,64(y);24,24(х);24,50(х);24,55(x);25,14(x);26,06(y);26,26(y);26,71(х);27,03(x);28,17(y);28,20(x);28,27(y);28,42(x);28,44(y);28,51(y);28,74(x);28,87(x);29,53(y);30,02(x);31,03(x);31,19(x);31,91(x);32,91(x);33,49(x);34,06(x);34,27(x);34,78(y);34,84(y);35,52(y);35,59(y);36,66(y);37,03(y);37,77(y);38,02(y);38,43(y);39,21(x);42,85(y)

U = 1 + 3 + 3 + 3 + 3 + 5 + 5 + 6 + 7 + 9 + 9 + 10 +10 + 10 + 10 + 10 + 10 + 10 + 10 + 19 = 153;

2) По формулам (23, 24) определяются расчетное и крити­ческое значение критерия Вилкоксона:

; ;

расчетное значение критерия Вилкоксона равно B_рас = 47.

; ;

3) По таблицам нормированной и центрированной кривой нормального распределения (Приложение 1) определяем аргумент по значению функции (Z_ = 1,96), критическое значение равно B_кр = 72,46.

Расчетное значение критерия Вилкоксона оказалось меньше критического. С учетом того, что критическая область данного критерия правосторонняя, принимаем нулевую гипотезу, которая подтверждает однородность сравниваемых совокупностей.

б) Использование критериев согласия преследует цель поиска закона распределения генеральной совокупности, которой принад­лежит данная анализируемая выборка. Расчеты проводятся для ис­ходной выборки (X) при N = 20. Цель расчетов заключается в сле­дующем: с помощью критерия согласия Пирсона проверить при­надлежность эмпирического материала нормальной кривой рас­пределения (кривая Гаусса). Основные положения по кривой рас­пределения приведены выше.

Как и при проверке однородности выдвигается нулевая ги­потеза, но в данном случае она утверждает согласие значений вы­борки со значениями нормальной кривой распределения, т. е. при увеличении данных натурных наблюдений до бесконечности, рас­пределение случайных чисел отвечает выбранному закону распре­деления. Расчет по критерию Пирсона основан на определении теоретической частоты в эмпирических интервалах, и если эмпи­рическая частота и теоретическая отличаются незначительно, то принимается нулевая гипотеза при выбранном уровне значимости и числе степеней свободы. Расчетная формула статистического критерия согласия Пирсона или ² имеет следующий вид:

,

(27)

где К — количество интервалов;

n_i — эмпирическая частота;

n_t — теоретическая частота.

Для того, чтобы использовать аналитические законы рас­пределения, необходимо знать область возможных значений слу­чайных величин (для нормально распределенной случайной вели­чины область возможных значений определяется интервалом (-; +)). Расчеты сводим в таблицу 4. При этом необходимо выпол­нить следующее условие: для граничных классов NP_i > 1, а для внутренних — NP_i > 5. Если условие не соблюдается, то классы необходимо укрупнять.

Таблица 4

Определение выборочного значения ²_рас на согласие эмпириче­ского распределения с нормальным законом распределения

N	аi	ni	bi		Фo(bi)		Pi	NPi	ni-NPi	2рас(i)
1	2	3	4		5		6	7	8	9
0	- - 18,86	0	-	-2,61	-0,50	-0,495	0,005	0,1	-0,10	0,1
1	18,86 - 22,93	1	-2,61	-1,59	-0,495	-0,44	0,055	1,1	-0,10	0,01
2	22,93 - 27,00	5	-1,59	-0,56	-0,44	-0,21	0,23	4,6	0,40	0,03
3	27,00 - 31,07	7	-0,56	0,46	-0,21	0,18	0,39	7,8	-0,80	0,08
4	31,07 - 35,14	6	0,46	1,49	0,18	0,43	0,25	5,0	1,00	0,20
5	35,14 - 39,21	1	1,49	2,51	0,43	0,494	0,064	1,28	-0,28	0,06
6	39,21 - +	0	2,51	+	0,494	+0,5	0,006	0,12	-0,12	0,12
							1,00	20,00	0,00	0,6

Условные обозначения:

a_i — границы интервалов;

n_i — эмпирическая частота;

b_i — нормированная и центрированная случайная вели­чина:

,

(28)

Ф_о(b_i) — значение функции нормального закона распреде­ления на границах интервалов определяется по таблицам (Прило­жение 1);

P_i — теоретическая вероятность попадания случайной величины в заданный интервал, P_i = Ф_о(b_i) - Ф_о(b_i-1);

N — объем выборки, N = 20;

NP_i — теоретическая частота.

Порядок определения табличных значений нормированного и центрированного нормального закона распределения. В таблице приложение 1 приведены значения функции в зависимости от аргумента Х. Столбец Х соответствует целому значению и десятой доли, строка –это сотая часть аргумента. Обратим внимание на нулевой столбец, он шире всех остальных за счет первых двух цифр (0,0; 0,1; 0,2; и т.д.). Это начало искомого значения функции. Трехзначное значение в столбиках – «хвост» который увеличивается по строке. Для определения значения функции необходимо по аргументу найти соответственное трехзначное значение и из «0» столбика подставить начало величины. Округлить полученное значение до двух знаков после запятой. Если аргумент отрицательная величина, то и перед значением функции должен быть поставлен знак минус.

В результате проведенных расчетов получили искомое расчетное значение критерия Пирсона ²_рас = 0,6.

Критическое значение критерия Пирсона определяется по таблицам (Приложение 3) или по формуле:

,

(29)

где m — число степеней свободы, m = K – 1;

Z_2 — коэффициент, определяемый по формуле:

,

(30)

, .

Учитывая это, критическое значение критерия Пирсона равно:

.

Критическое значение критерия Пирсона можно опреде­лить по таблицам ²-распределения в Приложении 3.

Если расчетное значение не превышает критического на выбранном уровне значимости нулевая гипотеза принимается, что подтверждает принадлежность исследуемой выборки нормальному закону распределения.