4. Графическое изображение вариационных рядов

Графическое изображение сгруппированных вариацион­ных рядов облегчает их анализ и позволяет в пер­вом приближении судить о форме кривой генеральной совокупно­сти. Для графического изображения рядов распределения приме­няют гистограмму (кривая распределения плотности вероятностей, дифференциальная кривая распределения). Гистограмма строится следующим образом: на оси абсцисс откладываются равные от­резки, которые в принятом масштабе соответствуют величинам границ интервалов вариационного ряда; на отрезках строятся пря­моугольники с высотами, равными приведенным частотам (приведенная частота - это относительная частота отнесенная к длине интервала, отно­сительная частота определяется делением эмпирической частоты каждого ин­тервала на объем выборки. Гистограмму принято преобразо­вывать в полигон распределения путем соединения середин верх­них сторон прямоугольников отрезками. График, построенный по результатам натурных наблюдений, обуславливает вид эмпириче­ской кривой распределения.

5. Изучение формы кривой распределения

Для получения приблизительного представления о форме кривой распределения строят гистограмму. Число наблюдений, по которому стро­ится эмпирическое распределение, обычно невелико и представ­ляет собой выборку из искомой генеральной совокупности. Эмпирические данные в определенной степени связаны со случай­ными ошибками, возникновение которых зачастую неизвестно, что искажает истинную закономерность изменение величины признака. При увеличении числа наблюдений одновременно с увеличением количества интервалов и уменьшением их длины полигон посте­пенно перерастает в кривую распределения.

Кривая распределения характеризует теоретическое (ана­литическое) распределение, т.е. распределение, которое получи­лось бы при полном погашении всех случайных причин, искажаю­щих основную закономерность. Исследование формы распределе­ния включает решение следующих задач:

1. определение общего характера распределения;

2. выравнивание эмпирического распределения (по­строение аналитической кривой распределения);

3. проверка соответствия найденного теоретического распределения эмпирическому.

В практике статистического исследования природоохран­ной деятельности приходится встречаться с самыми разными ви­дами распределений. Как правило, однородные совокупности имеют одновершинную форму, многовершинность свидетельст­вует о неоднородности изучаемой совокупности.

Выявление общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса. Для симметричных распределений среднее арифметическое, мода и медиана совпадают, коэффициент асим­метрии равен нулю (C_s = 0). При правосторонней (C_s > 0) между показателями центра распределения существует следующее соот­ношение М_o < М_е < Х_ср. Отрицательный знак показателя асиммет­рии (C_s < 0) свидетельствует о наличии левосторонней асимметрии. Между показателями центра распределения в этом случае имеем М_o > М_е > Х_ср. На рис.1 изображены кривые распределения, имею­щие различные значения коэффициента асимметрии .

Оценку степени существенности асимметрии выборки можно определить с помощью средней квадратичной ошибки, ко­торая зависит от объема наблюдений и рассчитывается по фор­муле:

.

(12)

Если отношение |C_s|/W_Cs > 3, асимметрия существенна и распределение признака в генеральной совокупности не является симметричным.

Рис.1. Кривые плотности распределения вероятностей

с различными значениями коэффициента асимметрии:

а — симметричная кривая C_s = 0;

б — асимметричная кривая при C_s < 0;

в — асимметричная кривая при C_s > 0.

Для симметричных распределений оценивается сущест­венность эксцесса. Эксцесс представляет собой выпад вершины кривой распределения плотности вероятностей вверх или вниз от вершины кривой нормального распределения (кривая Гаусса). Если вели­чина коэффициента эксцесса положительная, то распределение островершинное, отрицательная — плосковершинное. Средняя квадратичная ошибка эксцесса рассчитывается по формуле:

.

(13)

Если отношение |C_e|/W_Ce < 3, то эксцесс не свойственен рас­пределению признака в генеральной совокупности.

Оценка существенности показателей асимметрии и экс­цесса для генеральной совокупности (при |С_s| /W_Cs < 3, |C_e|/W_Ce<3) позволяет сделать вывод о возможном использовании для анализа эмпирического материала кривую нормального за­кона распределения (кривая Гаусса).

Если случайная величина имеет плотность распределения

,

(14)

то она подчиняется нормальному закону распределения. Нормаль­ное распределение является двух параметрическим, т.е. для его по­строения необходимо определить среднее арифметическое и сред­нее квадратическое отклонение. Данная функция затабулирована (приложение 1). Для получения функции распределения необходимо выражение 14 проинтегрировать. Для приведения кривых к одному началу случайные величины нормируются и центрируются по сле­дующему механизму: из каждого значения вариационного ряда вычитается среднее арифметическое, результат от разности де­лится на среднее квадратическое отклонение. В данном случае по­лученный новый ряд величин имеет следующие характеристики: X_ср = 0 и  = 1. Формула плотности распределения вероятностей нормированной и центрированной случайной величины запишется в следующем виде:

,

(15)

Данная функция затабулирована [3, 5, 17].

Приведем некоторые свойства нормальной кривой распре­деления:

1. Значения функции определены на всей протяженности число­вой прямой;

2. Кривая симметрична относительно максимальной ординаты;

3. Максимальная ордината соответствует М_о = М_е = Х_ср, а ее вели­чина равна 1/2;

4. Кривая асимптотически приближается к оси абсцисс, чем больше значения отклоняются от Х_ср, тем реже они встреча­ются;

5. Одинаковые по абсолютному значению, но противоположные по знаку отклонения случайной величины от среднего арифме­тического равновероятны;

6. Кривые имеют две точки перегиба, находящиеся на расстоянии  от Х_ср;

7. При Х_ср = сonst увеличением  кривая становится более поло­гой, при  = const с изменением Х_ср кривая не изменяет своей формы, а лишь сдвигается вправо или влево по оси абсцисс;

8. Отклонение случайной величины от среднего арифметического на  определяет площадь фигуры, равную 68,3% от общей площади, в промежутке Х_ср  2 находится 95,4% всех значений признака, Х_ср  3 приходится 99,7%.

Использование нормального закона распределения осно­вано на центральной предельной теореме, которая формулируется следующим образом: нормальное распределение возможно в том случае, когда на величину признака влияет большое число случай­ных факторов, действие этих факторов независимо, и ни одна из причин не имеет преобладающего влияния над другими.
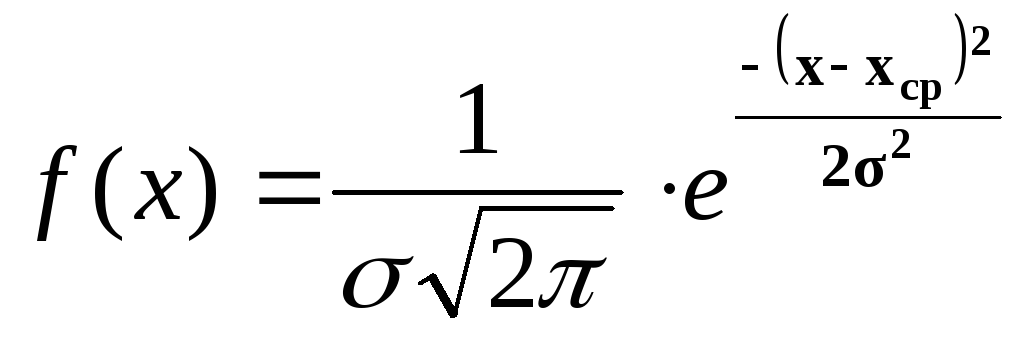