2. Прямые уровня

Прямые уровня – прямые параллельные одной из плоскостей проекций. Отрезки таких прямых, на плоскость проекций, которой они параллельны, проецируются без искажения – в натуральную величину.

Прямая, параллельная плоскости П₁ – горизонталь (рисунок 27). Фронтальная ее проекция параллельна оси Х. [А₁В₁]=[АВ] – длина отрезка. Углы наклона видны на чертежах.

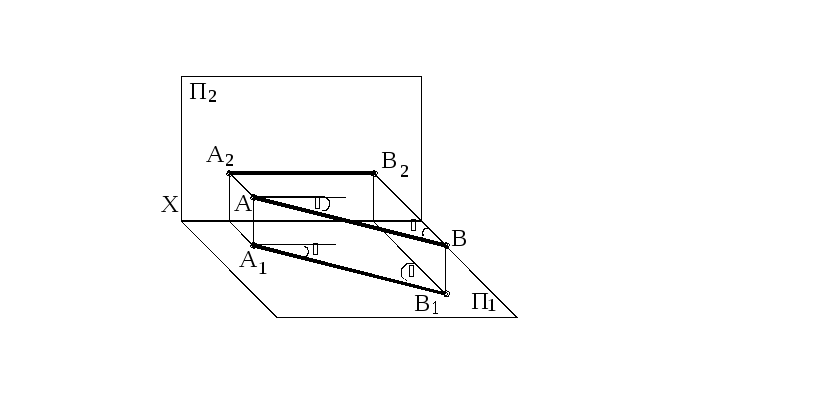
Рисунок 27

Прямая, параллельная плоскости П₂ - фронталь (рисунок 28). Горизонтальная ее проекция параллельная оси Х.

[А ₂ В₂]=[АВ]- длина отрезка.

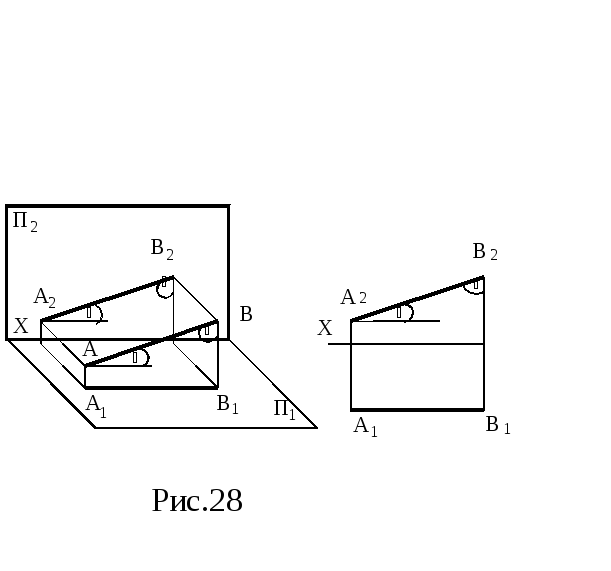
Рисунок 28

Прямая, параллельная плоскости П₃ – профильная прямая (рисунок 29).

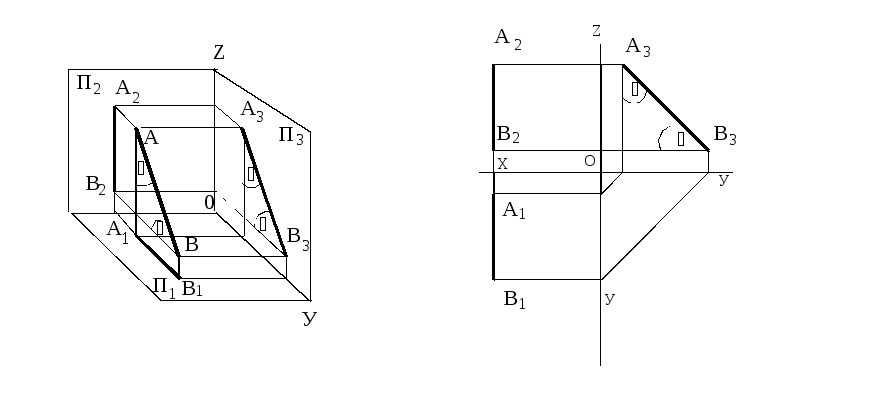
Рисунок 29

Горизонтальная и фронтальная проекции перпендикулярны оси Х.

[А₃В₃]=[АВ].

4.3 Проецирующие прямые

Проецирующие прямые – прямые перпендикулярные одной из плоскостей проекций и проецируются на эту плоскость в виде точки, а на две другие – в натуральную величину.

Горизонтально проецирующая прямая- прямая, перпендикулярная плоскости проекций П₁ (рисунок 30).

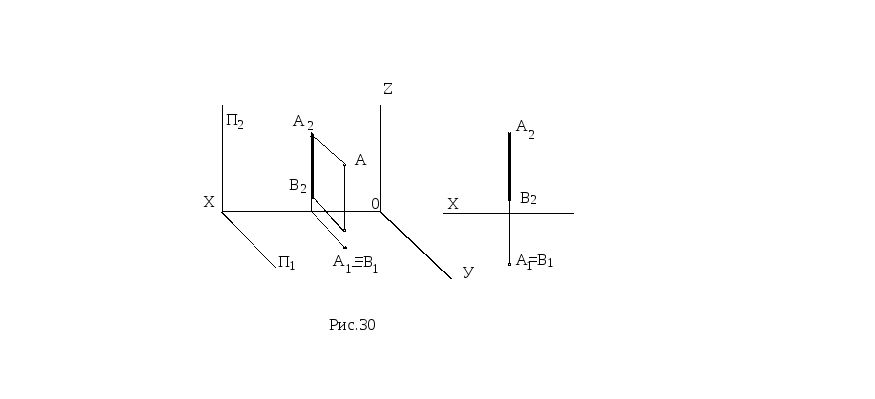
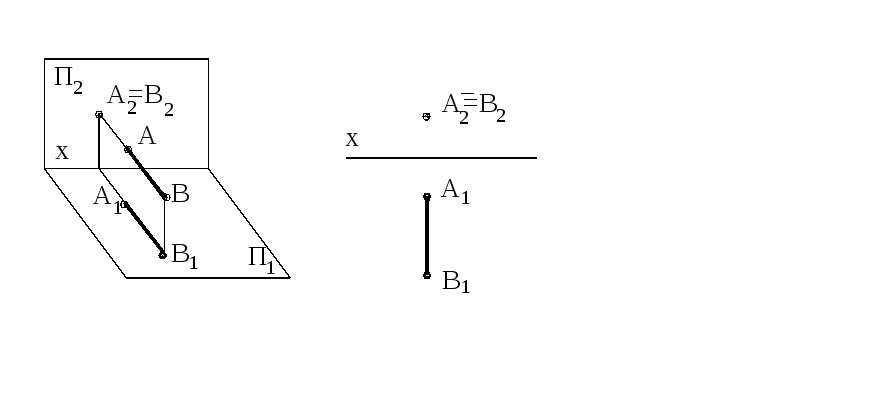
Рисунок 30 Рисунок 31

Фронтально проецирующая прямая – прямая, перпендикулярная плоскости проекций П₂ (рисунок 31).

Профильно - проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций П₃ (рисунок 32).

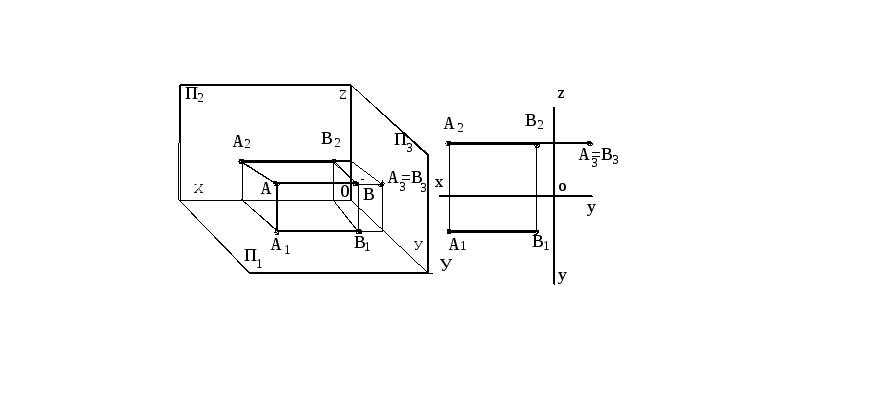
Рисунок 32

Как видно из чертежей (рисунки 27-32), если прямая занимает частное положение, то на чертеже видны длины отрезков и величины углов наклона ее к плоскостям проекций

4.4 Следы прямой

Следы прямой - это точки пересечения прямой с плоскостями проекций. Горизонтальный след прямой M=M₁ – точка пересечения прямой m с плоскостью проекций П₁. Фронтальный след прямой N=N₂ – точка пересечения прямой m с плоскостью проекций П₂. Профильный след прямой плоскостям проекций.

Р=Р₃ - точка пересечения прямой АВ с плоскостью проекций П₃.Чтобы построить горизонтальный след М прямой АВ (рисунки 33, 34) нужно продолжить фронтальную проекцию А₂В₂ до пересечения с осью Х и из точки М₂ (фронтальная проекция горизонтального следа) восстановить перпендикуляр к оси Х до пересечения с горизонтальной проекцией А₁В₁. Точка М₁ (горизонтальная проекция горизонтального следа) совпадает с самим следом М.

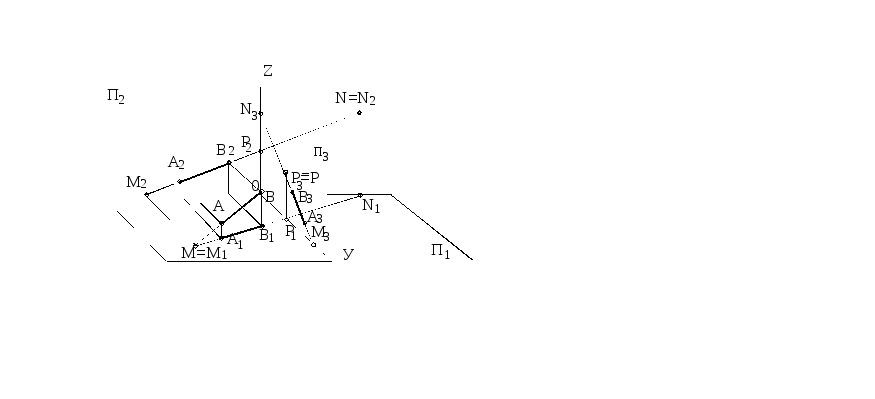
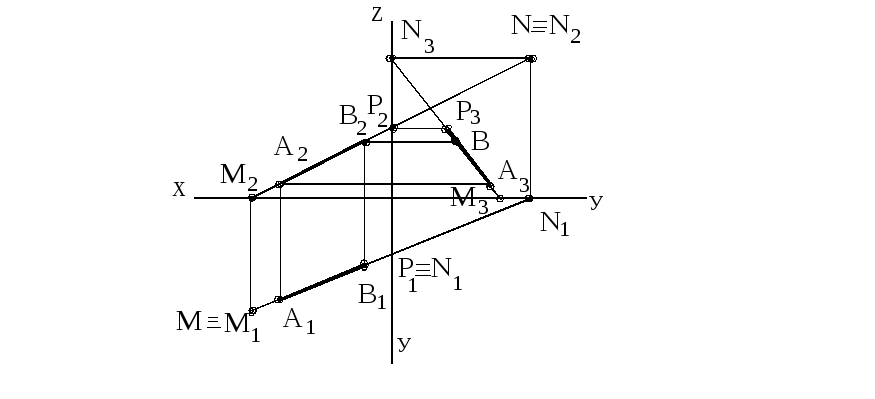
Рисунок 33 Рисунок 34

5 Взаимное положение прямых

Две прямые могут пересекаться между собой , могут быть параллельными и могут скрещиваться.

Пересекающиеся прямые – это прямые, которые имеют одну общую точку пересечения. Характерным признаком этих прямых на ортогональном чертеже является:

1. одноименные проекции прямых пересекаются;

2. точки пересечения одноименных проекций лежат на одном перпендикуляре к оси Х (рисунок 35).

Параллельные прямые – это прямые, у которых одноименные проекции параллельны между собой (рисунок 36).

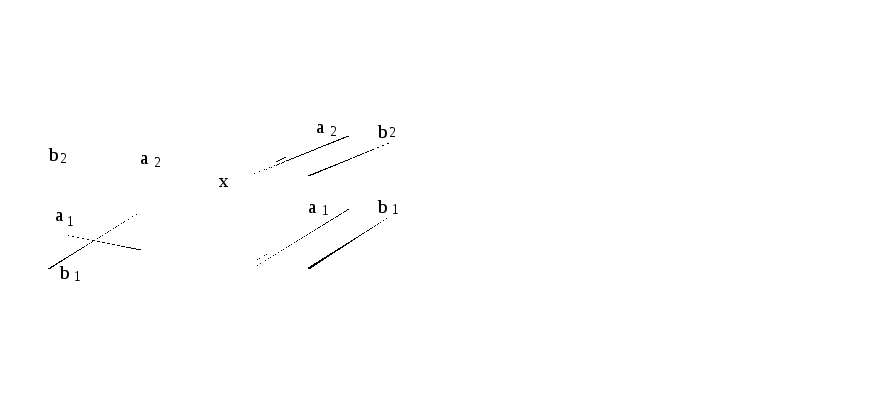
Рисунок 35 Рисунок 36

Этого условия достаточно для прямых общего положения, но недостаточно для прямых частного положения. Чтобы определить взаимную параллельность прямых частного положения в пространстве, необходимо иметь их проекции на ту плоскость, которой они параллельны (рисунок 37).

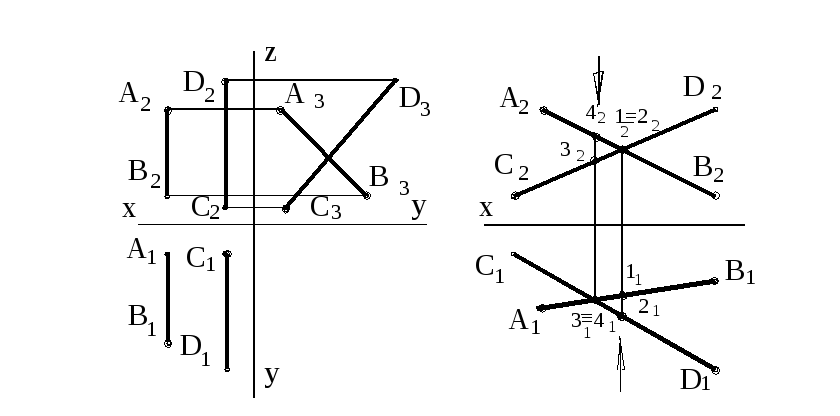
Рисунок 37 Рисунок 38

На рисунке 37 видно, что прямые не параллельны друг другу, так как фронтальные их проекции не параллельны.

Скрещивающиеся прямые - это прямые, которые лежат в двух разных плоскостях. Характерным признаком этих прямых является:

1. точки пересечения одноименных проекций прямых не расположены на одном перпендикуляре к оси проекции, так как это проекции двух точек, лежащих на разных прямых (рисунок 38);

2. одноименные проекции не параллельны между собой (рисунок 39). Одна пара одноименных проекций может быть взаимно параллельна.

Рисунок 39

Точки, у которых какие-либо одноименные проекции совпадают на эпюре, называются конкурирующими. Эти точки принадлежат одному проецирующему лучу. Например точки 1 и 2; 3 и 4 (рисунок 38). С помощью конкурирующих точек определяется видимость самих точек и прямых, на которых расположены эти точки. Они принадлежат разным прямым АВ и СD.

У точек 1 и 2 совпадают их фронтальные проекции, у точек 3 и 4 – горизонтальные. На фронтальной плоскости проекций точка 2 закрывает собой точку1, так как точка 2 удалена от плоскости П₂ дальше, чем точка 1. На горизонтальной плоскости проекций точка 4 закрывает собой точку 3, так как точка 4 удалена от плоскости П₁ дальше, чем точка 3.