18 Пересечение прямой линии с поверхностью

18.1 Частные случаи

Разберем несколько частных случаев пересечения прямой линии с поверхностью. Характерными для них являются перпендикулярность ребер или образующих поверхности или самой прямой к одной из плоскостей проекций. Вследствие этого, одна из проекций искомых точек пересечения ( точек «входа» и «выхода») определяется без дополнительных построений и остается построить по ней другую проекцию.

На рисунок 109 даны проекции прямой призмы, стоящей основанием на горизонтальной плоскости проекций. Так как боковые грани призмы занимают горизонтально проецирующее положение, то горизонтальная проекция точек пересечения заданной прямой с поверхностью призмы (1₁ и 2₁) определяются без дополнительных построений, а фронтальные проекции (1₂ и 2₂) находятся из условия принадлежности точек заданной прямой.

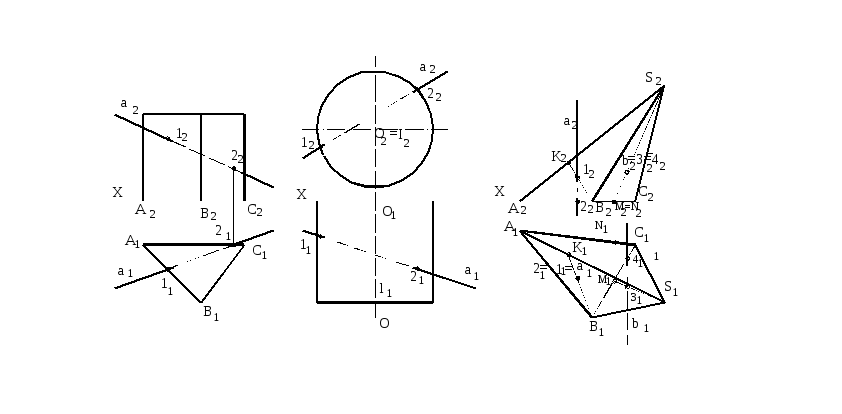
Рисунок 109 Рисунок 110 Рисунок 111

На рисунке 110 даны проекции прямого цилиндра, занимающего фронтально проецирующее положение. Поэтому фронтальные проекции точек пересечения заданной прямой с поверхностью цилиндра (1₂ и 2₂) определяются без дополнительных построений, а горизонтальные проекции точек 1₁ и 2₁– по принадлежности точек прямой.

На рисунке 111 прямая а перпендикулярна П₁, поэтому горизонтальные проекции точек ее пересечения с гранью и основанием пирамиды совпадают (1₁=2₁). Фронтальная проекция одной из них (2₂), принадлежащая основанию пирамиды, находится на фронтальной проекции основания. Для построения фронтальной проекции точки 1₂, лежащей на боковой грани, достаточно через проекцию 1₁ провести любую прямую, принадлежащую этой грани. Фронтальная проекция 1₂ будет находиться на фронтальной проекции введенной прямой.

Аналогичный пример приведен на рисунке 111, где прямая b перпендикулярна к плоскости П₂, поэтому проекции 3₂ и 4₂ искомых точек определяются без дополнительных построений. Горизонтальная проекция 3₁ определена с помощью дополнительной прямой SM, проведенной через проекцию 3₂ , а 4₁ - c помощью дополнительной прямой SN, проведенной через проекцию 4_{2 .}

18.2 Общие случаи

Если заданы прямая общего положения и поверхность общего положения, то для определения точек их пересечения (точки входа и точки выхода), нужно несколько раз решить задачу на пересечение прямой общего положения (ребер или образующих) с проецирующей плоскостью, проведенной через заданную прямую. Полученные точки соединить, учитывая видимость поверхности относительно плоскостей проекций.

Алгоритм решения

Чтобы определить точки пересечения прямой общего положения с геометрическим телом нужно:

1. Через прямую ввести плоскость (удобную для решения).

2. Построить проекции сечения введенной плоскости с заданной поверхностью.

3. Найти точки пересечения заданной прямой с контуром фигуры сечения. Это и будут искомые точки входа и выхода.

Пример определения точек пересечения прямой с призмой приведен на рисунке 112.

Призма пересекается прямой MN. Для определения точек пересечения K и F прямой MN с поверхностью призмы:

Через прямую MN проведена плоскость Р.

Найдено сечение поверхности призмы плоскостью P – треугольник 123.

Точки пересечения прямой MN с контуром сечения (с линией пересечения) – K, R и будут точками входа и выхода. На рисунке 113 показано нахождение точек пересечения прямой МN с поверхностью наклонной призмы

Через прямую МN проведена фронтально проецирующая плоскость P (на чертеже задана фронтальным следом Р₂).

Построено сечение поверхности призмы плоскостью P – треугольник 123.

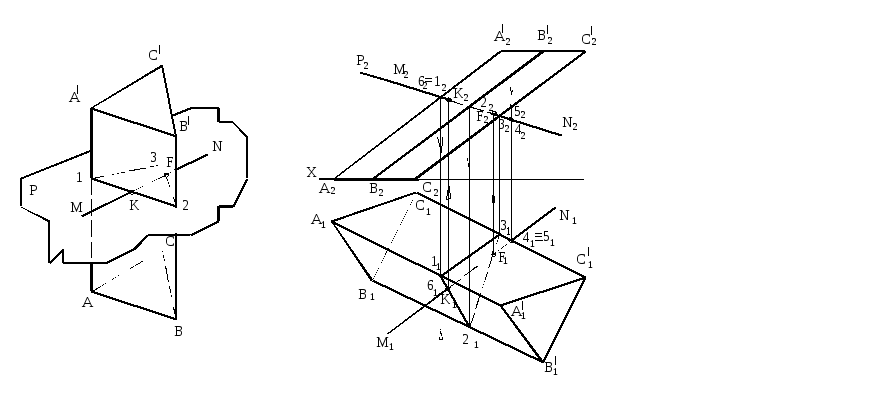
Рисунок 112 Рисунок 113

Определены точки K и F пересечения прямой MN с поверхностью наклонной призмы.

Определена видимость прямой: на горизонтальной проекции с помощью конкурирующих точек 4 и 5; на фронтальной проекции – с помощью конкурирующих точек 6 и 1.

Иногда задачи решаются проще, если вместо вспомогательной проецирующей плоскости через заданную прямую провести плоскость общего положения.

Пример. Найти точки пересечения прямой АВ общего положения с поверхностью наклонного цилиндра (рисунок 114).

Рисунок 114

Решение:

Через заданную прямую АВ проведена вспомогательная плоскость Р, параллельная образующим цилиндра.

Плоскость Р задана двумя пересекающимися прямыми АВ и а. Прямая а проведена параллельно образующим поверхности цилиндра.

Построена фигура сечения цилиндра с плоскостью Р.

Для этого, найден горизонтальный след плоскости Р – Р₁. На пересечении следа Р₁ с основанием цилиндра определены проекции точки 1₁ и 2₁. Через эти точки и пройдут горизонтальные проекции образующих, по которым вспомогательная плоскость Р рассекает поверхность цилиндра.

В пересечении образующих, проходящих через проекции точек 1₁ и 2₁, с проекцией А₁В₁ получены проекции точек K₁ и F₁ – горизонтальные проекции точек пересечения прямой АВ с поверхностью наклонного цилиндра. Фронтальные проекции K₂ и F₂ определятся по принадлежности этих точек заданной прямой АВ.

Определена видимость прямой, относительно поверхности, цилиндра методом конкурирующих точек.