
- •Математика
- •Теоретические вопросы к экзамену по дисциплине « Математика» для студентов
- •Курса очной формы обучения. ( 1 семестр )
- •Тема 1. Линейная алгебра.
- •1). Решить систему методом Крамера :
- •2). Решить систему методом Гаусса :
- •Тема 2.Элементы аналитической геометрии.
- •Тема3. Введение в анализ функции одной переменной.
- •Тема4. Дифференциальное исчисление функции одной переменной.
- •1). Найти производную функции:
- •1). Найти производную функции:
- •1). Найти производную функции:
- •Формы контроля знаний студентов по дисциплине « Математика»
- •Теоретические вопросы к зачёту по дисциплине« Математика» для студентов
- •1 Курса очной формы обучения. ( 2 семестр )
- •Тема 5. Комплексные числа
- •Тема 6. Дифференциальное исчисление функции нескольких переменных
- •Тема 7. Интегральное исчисление.
- •1. Первообразная, неопределенный интеграл и их свойства
- •Свойства неопределенного интеграла
- •3). Интегрирование рациональных функций
- •5). Интегрирование некоторых иррациональных функций
- •4. Определенный интеграл.
- •1.Вычисление площадей плоских фигур.
- •2.Вычисление объёмов тел вращения.
- •1. Задания по линейной алгебре
- •2. Задания по аналитической геометрии
- •3. Задания по математическому анализу (1) Вопросы для самопроверки
- •2. Задания по математическому анализу
- •Содержание.
Тема3. Введение в анализ функции одной переменной.
![]()
![]()
![]()
![]()
Неопределённости:
![]()

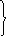 -
эквивалентности
-
эквивалентности
![]()
![]() -
первый замечательный предел
-
первый замечательный предел
![]()
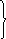
![]() второй
замечательный предел
второй
замечательный предел
![]()
![]()
![]() разложить
на множители функцию; до множить
числитель и знаменатель до формулы
сокращённого умножения.
разложить
на множители функцию; до множить
числитель и знаменатель до формулы
сокращённого умножения.
![]() если
это отношение многочленов, то числитель
и знаменатель разделить на переменную
в наивысшей степени.
если
это отношение многочленов, то числитель
и знаменатель разделить на переменную
в наивысшей степени.
![]() - свести к дробным неопределённостям.
- свести к дробным неопределённостям.
Опр. Функция
![]() является непрерывной в точке
является непрерывной в точке
![]() ,
если она:
,
если она:
1. определена в точке
![]()
2. имеет конечный предел при
![]()
3.
![]()
![]()
Если
![]()
![]() ,
то
,
то
![]() является непрерывной слева в точке
является непрерывной слева в точке
![]() .
.
Если
![]() ,
то
,
то
![]() является непрерывной справа в точке
является непрерывной справа в точке
![]() .
.
Точка
![]() -
называется точкой разрыва 1-го рода
функции
-
называется точкой разрыва 1-го рода
функции
![]() ,
если функция имеет конечные, но не равные
друг другу правый и левый пределы.
,
если функция имеет конечные, но не равные
друг другу правый и левый пределы.
![]()
![]() ,
,
![]()
![]() ,
,
![]() - скачок функции.
- скачок функции.
Точка
![]() -
называется точкой разрыва 2-го рода
функции
-
называется точкой разрыва 2-го рода
функции
![]() ,
если в этой точке функция не имеет по
крайней мере одного из односторонних
пределов или хотя бы один из них равен
бесконечности.
,
если в этой точке функция не имеет по
крайней мере одного из односторонних
пределов или хотя бы один из них равен
бесконечности.
Т-3 С-1
1). Вычислить пределы:
а) lim
![]() ; б) lim
; б) lim
![]() ; в) lim x·ctg2x
; в) lim x·ctg2x
x→0 x→∞ x→0
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
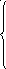
 ³x+1,
если x ≤ 0
³x+1,
если x ≤ 0
y = -x + 1, если 0 < x < 2
1 , если x ≥ 2
x
Т-3 С-2
1). Вычислить пределы:
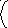




 а) lim x³
_ x ; б) lim
1 - √1-x ; в) lim
√2x - x
а) lim x³
_ x ; б) lim
1 - √1-x ; в) lim
√2x - x
 x→∞ x²
+ 1 x→0 sin4x
x→0 tg√x
x→∞ x²
+ 1 x→0 sin4x
x→0 tg√x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
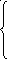
1 , если x<0
x
y = х, если 0≤x<1
-х, если x≥
Т-3 С-3
1). Вычислить пределы:

 а) lim 1 + x –
3 x³ ; б)
lim x ; в) lim
sin2x·ctgx
а) lim 1 + x –
3 x³ ; б)
lim x ; в) lim
sin2x·ctgx
x→∞ 1 + x² + 3x³ x→0 2 - √x+4 x→π
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
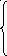
x², если x ≤ 0
y = -x², если 0 < x ≤ 1
x + 1, если x > 1
Т-3 С-4
1). Вычислить пределы:

 а) lim x³
+ 3x² + 2x
; б) lim x²
- √x ; в) lim
sin(x+1)
а) lim x³
+ 3x² + 2x
; б) lim x²
- √x ; в) lim
sin(x+1)
x→ -2 x² - x - 6 x→1 √x - 1 x→ -1 1 - x²
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 x³, если x
≤ 1
x³, если x
≤ 1

y = √x , если 1 < x ≤ 2
3, если x
Т-3 С-5
1). Вычислить пределы:
а
 )
lim 8x³ -
1 ; б) lim √x-1
- 2 ; в) lim sin5x
)
lim 8x³ -
1 ; б) lim √x-1
- 2 ; в) lim sin5x
x→ ½ 6x² - 5x + 1 x→5 x - 5 x→0 x + x²
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
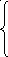 1, если x < 0
1, если x < 0
y = x
2, если 0 x < 1≤1
x, если x ≥ 1
Т-3 С-6
1). Вычислить пределы:
а) lim x² - 2x + 1 ; б) lim 4x² + x - 5 ; в) lim tg х/2
 x→ 1 x³
- x x→∞
x³ - 1 x→0
sin2x
x→ 1 x³
- x x→∞
x³ - 1 x→0
sin2x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
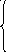 -3x, если x
< 0
-3x, если x
< 0
y = 2x, если 0 ≤ x < 1
x², если x ≥ 1
Т-3 С-7
1). Вычислить пределы:
а) lim x - 7 ; б) lim 1 + 3x² ; в) lim 2arcsin2x
x→ 7 49 - x² x→∞ 2x - 5 x→0 3x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 x – 1, если x
< -2
x – 1, если x
< -2
y = 1 , если –2 ≤ x < 0
x
x , если x ≥ 0
Т-3 С-8
1). Вычислить пределы:
а) lim 4 – 5x ; б) lim 9 - x² ; в) lim tgk·x
x→∞ 3 – 2x x→-3 x + 3 x→0 x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
1 - x², если x < 0
y = 4 – x , если 0 ≤ x ≤ 2
(x - 1)² , если x > 2
Т-3 С-9
1). Вычислить пределы:
а) lim 5x² – 3x + 1 ; б) lim x + 3 x ; в) lim x – 2
 x→∞ 3x²
+ x - 5 x→
∞ x - 2 x→2
√2x - 2
x→∞ 3x²
+ x - 5 x→
∞ x - 2 x→2
√2x - 2
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 - 2x, если x
≤ 0
- 2x, если x
≤ 0
y = √x , если 0 < x
< 4
= √x , если 0 < x
< 4
1, если x ≥ 4
Т-3 С-10
1). Вычислить пределы:


 а) lim 4x5
– 2x3 + 2
; б) lim 2x
- 1 x ; в) lim
√2x-1 -
√5
а) lim 4x5
– 2x3 + 2
; б) lim 2x
- 1 x ; в) lim
√2x-1 -
√5
x→∞ x5 + 3 x→ ∞ 2x + 1 x→3 x - 3
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 - x, если x
≤ 0
- x, если x
≤ 0
y = - (x - 1)² , если 0 < x < 2
x – 3, если x ≥ 2
Т-3 С-11
1). Вычислить пределы:


а) lim x3 + 1 ; б) lim 4x 1 2x ; в) lim 1 - √1- x²
x→∞ 2x3 + 1 x→ ∞ 4x x→0 x²
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 x + 2, если x
≤ -1
x + 2, если x
≤ -1
y = x² + 1 , если -1 < x ≤ 1
-x + 3, если x > 1
Т-3 С-12
1). Вычислить пределы:
а) lim 1 – 2x ; б) lim x ; в) lim (1 + 2x)1/x
 x→∞ 3x
- 2 x→ 0 √ 1-3x
- 1 x→0
x→∞ 3x
- 2 x→ 0 √ 1-3x
- 1 x→0
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 x + 4, если x
< -1
x + 4, если x
< -1
y = x² + 2 , если –1 ≤ x < 1
2x , если x ≥ 1
Т-3 С-13
1). Вычислить пределы:

 а) lim
а) lim![]() ; б) lim 1+ x
+
; б) lim 1+ x
+
![]() ; в) lim tg2x
; в) lim tg2x
x→0 x→∞ x³ - 3 x→0 х
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:

 ³x-1,
если x ≤ 0
³x-1,
если x ≤ 0
y = x - 1, если 0 < x < 1
1 , если x ≥ 1
x![]()
Т-3 С-14
1). Вычислить пределы:




 а) lim x³
_ x ; б) lim
1 - √1+x ; в) lim
√2x - x
а) lim x³
_ x ; б) lim
1 - √1+x ; в) lim
√2x - x
x→∞ x² - 1 x→0 sin3x x→0 tg√2x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 3 , если x<0
3 , если x<0
x
y = 2х, если 0≤x<1
-х, если x≥1
Т-3 С-15
1). Вычислить пределы:

 а) lim 1 + x –
3 x³ ; б)
lim 4 x ; в) lim sin5x·ctg3x
а) lim 1 + x –
3 x³ ; б)
lim 4 x ; в) lim sin5x·ctg3x
x→∞ 1 + x² + 3x³ x→0 2-√x+4 x→π
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 -x², если x
≤ 0
-x², если x
≤ 0
y = x², если 0 < x ≤ 1
-x + 1, если x > 1
Т-3 С-16
1). Вычислить пределы:

а) lim x³ + 3x² + 2x ; б) lim x² - √x ; в) lim sin(x-1)
 x→ -2 x²
- x - 6 x→1
1-√x x→
1 1 - x²
x→ -2 x²
- x - 6 x→1
1-√x x→
1 1 - x²
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
- x³, если x ≤ 1

y = √x , если 1 < x ≤ 2
2, если x >2
Т-3 С-17
1). Вычислить пределы:

а )
lim 8x³
+ 1 ; б) lim √х-1
- 1 ; в) lim sin4x
)
lim 8x³
+ 1 ; б) lim √х-1
- 1 ; в) lim sin4x
x→ -½ 6x² + 5x + 1 x→2 x - 2 x→0 x + x²
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 1 , если x < 0
1 , если x < 0
2x
у = 1 , если 0≤ x < 1
0,5x, если x ≥ 1
Т-3 С-18
1). Вычислить пределы:
а) lim x² + 2x + 1 ; б) lim 5x² + x + 9 ; в) lim tg х/5
 x→ -1 x
x→ -1 x![]() + x x→∞
x³ + 1 x→0
sin3x
+ x x→∞
x³ + 1 x→0
sin3x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 3x, если x
< 0
3x, если x
< 0
y = -2x, если 0 ≤ x < 1
-x², если x ≥ 1
Т-3 С-19
1). Вычислить пределы:
а) lim x - 6 ; б) lim 1 - 3x² ; в) lim 2arcsin23x
x→ 6 36 - x² x→∞ 7x - 5 x→0 3x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 x -2, если x
< -2
x -2, если x
< -2
y = 1 , если –2 ≤ x < 0
2x
3x , если x ≥ 0
Т-3 С-20
1). Вычислить пределы:
а) lim 4 + 5x ; б) lim 9 - x² ; в) lim tg5·x
x→∞ 1 + 2x x→3 x - 3 x→0 x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
1 + x², если x < 0
y = 4 + x , если 0 ≤ x ≤ 2
(x + 1)² , если x > 2
Т-3 С-21
1). Вычислить пределы:

 а) lim x²
– 3x + 1 ; б) lim
x + 3 x
; в) lim 2x
– 2
а) lim x²
– 3x + 1 ; б) lim
x + 3 x
; в) lim 2x
– 2
 x→∞ 3x²
- x - 4 x→
∞ x + 1 x→1
√2x -
x→∞ 3x²
- x - 4 x→
∞ x + 1 x→1
√2x -
![]()
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 - x, если x
≤ 0
- x, если x
≤ 0
y = √2x , если 0 < x
< 4
= √2x , если 0 < x
< 4
3, если x ≥ 4
Т-3 С-22
1). Вычислить пределы:


 а) lim x5
– x3 + 2
; б) lim 2x
+ 1 x ; в) lim
√2x-1 -
√3
а) lim x5
– x3 + 2
; б) lim 2x
+ 1 x ; в) lim
√2x-1 -
√3
x→∞ 2x5 + 3 x→ ∞ 2x - 1 x→2 x - 2
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 -2 x, если x
≤ 0
-2 x, если x
≤ 0
y = - (x + 1)² , если 0 < x < 2
x – 2, если x ≥ 2
Т-3 С-23
1). Вычислить пределы:


а) lim 4x3 + 1 ; б) lim 4x - 1 2x ; в) lim 1 - √1+ x²
x→∞ x3 + 1 x→ ∞ 4x x→0 x²
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 x - 2, если x
≤ -1
x - 2, если x
≤ -1
y = x² - 1 , если -1 < x ≤ 1
x - 3, если x > 1
Т-3 С-24
1). Вычислить пределы:
а) lim 1 +4x ; б) lim 3 x ; в) lim (1 - 2x)1/x
 x→∞ 3x -
2 x→ 0 √ 1-3x
- 1 x→0
x→∞ 3x -
2 x→ 0 √ 1-3x
- 1 x→0
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 x + 3, если x
< -1
x + 3, если x
< -1
y = x² + 1 , если –1 ≤ x < 1
x , если x ≥ 1
Т-3 С-25
1). Вычислить пределы:
 а) lim
а) lim
![]() ; б) lim 5- x
- 8
; б) lim 5- x
- 8![]() ; в) lim x·ctg8x
; в) lim x·ctg8x
x→0 x→∞ 7x³ + 7 x→0
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 ³x-4,
если x ≤ 0
³x-4,
если x ≤ 0
y = -2x +2, если 0 < x < 2
5 , если x ≥ 2
x
Т-3 С-26
1). Вычислить пределы:





 а) lim x³
_ 4x ; б) lim
1 - √1-x ; в) lim
√2x - 3x
а) lim x³
_ 4x ; б) lim
1 - √1-x ; в) lim
√2x - 3x
x→∞ x² + 1 x→0 sin3x x→0 tg√3x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:

1 , если x<0
x
y = 4х, если 0≤x<1
-3х, если x≥1
Т-3 С-27
1). Вычислить пределы:
 а) lim 9 + x –2
x³ ; б) lim
x ; в) lim sin2x·ctg5x
а) lim 9 + x –2
x³ ; б) lim
x ; в) lim sin2x·ctg5x
 x→∞ 7 - x²
+x³ x→0
3 - √x+9 x→π
x→∞ 7 - x²
+x³ x→0
3 - √x+9 x→π
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 2x², если x
≤ 0
2x², если x
≤ 0
y = -3x², если 0 < x ≤ 1
2x + 1, если x > 1
Т-3 С-28
1). Вычислить пределы:
а) lim x³ + 3x² + 2x ; б) lim x - 4 ; в) lim sin(x-1)
 x→ -2 x²
- x - 6 x→4
√x - 2 x→
1 1 - x²
x→ -2 x²
- x - 6 x→4
√x - 2 x→
1 1 - x²
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:

0,5 x³, если x ≤ 1

y = - √x , если 1 < x ≤ 2
-3, если x >2
Т-3 С-29
1). Вычислить пределы:

а) lim 8x³ - 1 ; б) lim √x-1 - 2 ; в) lim sin9x
x→ ½ 6x² - 5x + 1 x→5 x - 5 x→0 x + x²
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
 - 1, если x < 0
- 1, если x < 0
y = x
4, если 0 x < 1≤1
-2x, если x ≥ 1
Т-3 С-30
1). Вычислить пределы:
а) lim x² - 2x + 1 ; б) lim x² + 3x - 5 ; в) lim tg х/3
 x→ 1 x³
- x x→∞
5x³ + 1 x→0
sin8x
x→ 1 x³
- x x→∞
5x³ + 1 x→0
sin8x
2). Найти точки разрыва функции, если они существуют. Сделать чертёж:
-2x, если x < 0
y = 3x, если 0 ≤ x < 1
-2x², если x ≥ 1
