5). Интегрирование некоторых иррациональных функций

Рассмотрим интеграл вида

(6)

где R - рациональная функция, а, b - постоянные, τ, s - целые положительные числа. Обозначим m - наименьшее общее кратное чисел s₁,…,s_k с помощью подстановки ах+b=t^m интеграл (6) приводится к интегралу от рациональной функции новой переменной t.

Пример З. Сделаем в интеграле замену переменной .

Получаем , и наш интеграл преобразуется следующим образом:

В интегралах вида можно избавиться от иррациональности ответственно подстановками .

Пример 4. В интеграле рационально сделать замену переменной , тогда

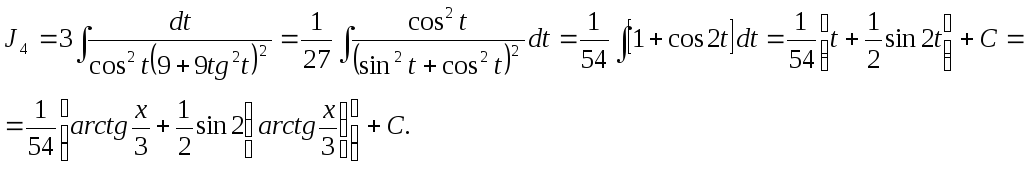
Пример5. Вычислить интеграл .

Сделаем замену переменной ,

Тогда

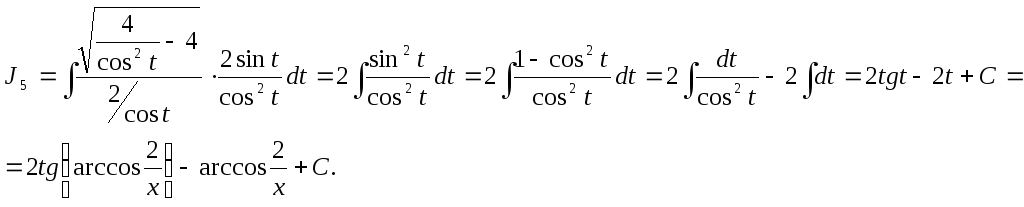
Этот ответ можно еще преобразовать. Так как

то окончательно имеем

Наряду с указанными подстановками можно использовать и другие.

Пример 6. Интеграл

Вычисляется с помощью подстановки .

В этом случае

4. Определенный интеграл.

.

Свойства определенного интеграла

Если функция f(x) интегрируема на отрезке [a, b], то ее интеграл является числом, не зависящим от выбора обозначения для аргумента подынтегральной функции, т.е. от обозначения переменной интегрирования:

Для любой функции f(x), определенной в точке a, положим по определению .

Кроме того, для функции f(x), интегрируемой на [a, b], будем считать по определению, что .

Приведем без доказательства основные свойства определенного интеграла.

Свойство 1 (свойство линейности)

Если функции f(x) и g(x) интегрируемы на отрезке [а, b], то для любых вещественных чисел α и β справедливо равенство:

Свойство 2 (свойство адаптивности)

Если функция f(x) интегрируема на отрезках [a, b] и [с, d], то она интегрируема и на отрезке [a, d]. Причем

Свойство 3 (основная теорема интегрального исчисления)

Если функция f(x), непрерывна на отрезке [а, b] и F(x)- какая-нибудь первообразная для f(x) на этом отрезке. то справедлива формула Ньютона-Лейбница

(1)

Заметим, что такое название формулы (1) условно, т.к. ни у Ньютона, ни у Лейбница такой формулы в точном смысле этого слова нет. Но важно, что именно Ньютон и Лейбниц впервые установили связь между интегрированием и дифференцированием, позволяющую создать правило для вычисления определенных интегралов.

Символ называется знаком двойной подстановки. С его помощью формула (1) записывается так:

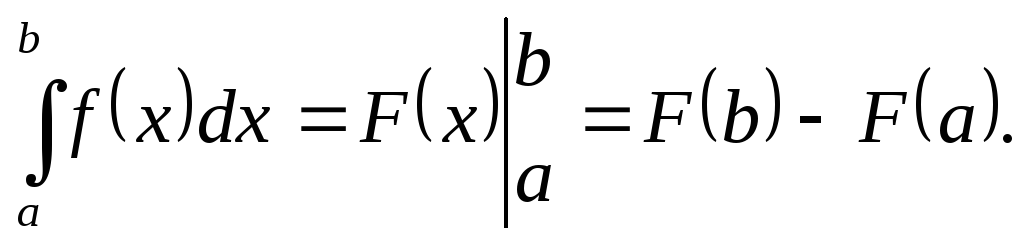
Пример 1. Вычислить следующие определенные интегралы по формуле (1):

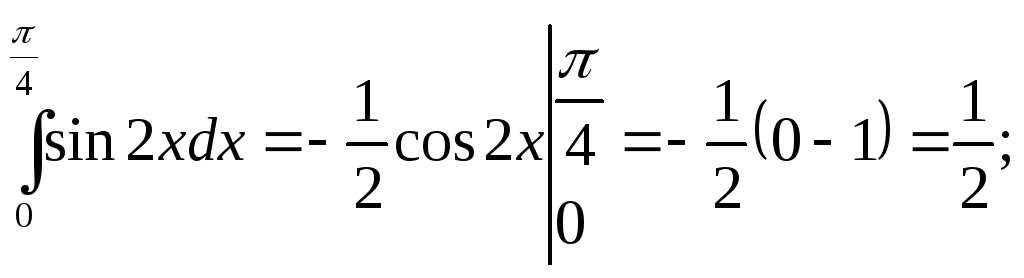
Геометрические приложения определенного интеграла.

1.Вычисление площадей плоских фигур.

a)

у y=f(x) S=

0 a b х

б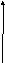) у

f(x) g(x)

S=

0 a c b х

у

в) 0 a b х

S= -

f(x)

г) у

f(x)

S=

g(x)

0 a b х