4.2 Метод Гаусса решения систем линейных уравнений
Рассмотрим
ещё один метод решения систем линейных
уравнений (17). С помощью элементарных
преобразований над строками расширенная
матрица системы (17)
может быть приведена к виду
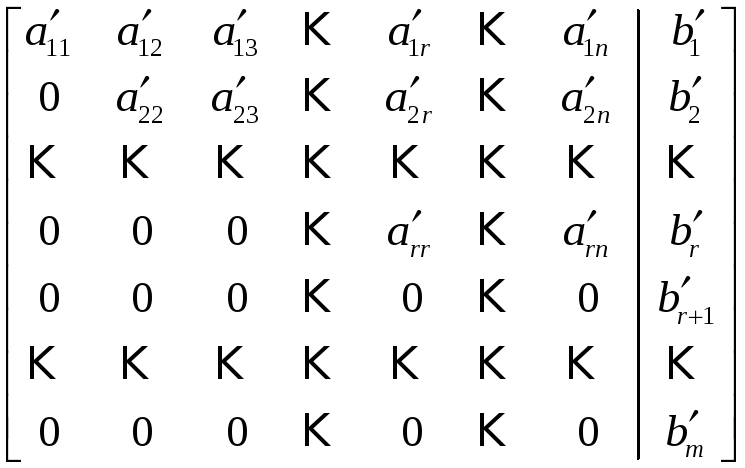. (21)
Эта матрица является расширенной матрицей системы
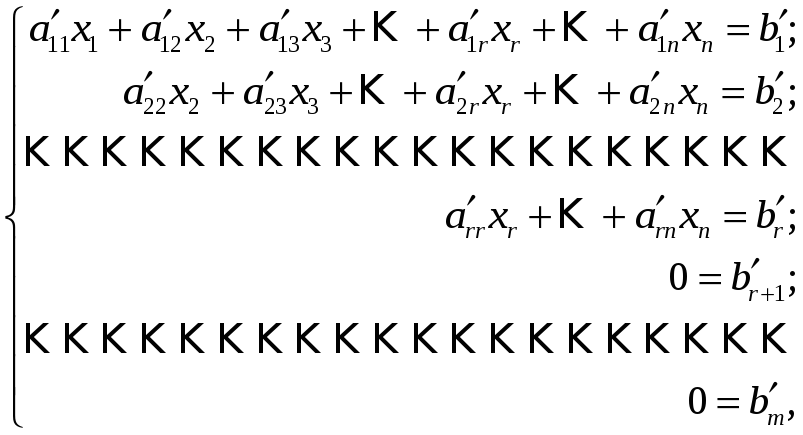(22)
которая эквивалентна исходной системе (17). Проанализируем систему уравнений (22).
Если
хотя бы одно из чисел
,…,
отлично от нуля, то система (22), а
следовательно, и система (17) несовместны,
так как
.
Если
же
…
,
то система совместна, так как
,
и из системы (22) можно выразить базисные
неизвестные, в данном случае
через свободные неизвестные
.
4.2.1 Пример. Методом Гаусса исследовать совместность и найти общее решение системы (20).
Решение.
С
помощью элементарных преобразований
строк расширенную
матрицу
системы уравнений (20)
приведём к
виду, подобному (21):
.
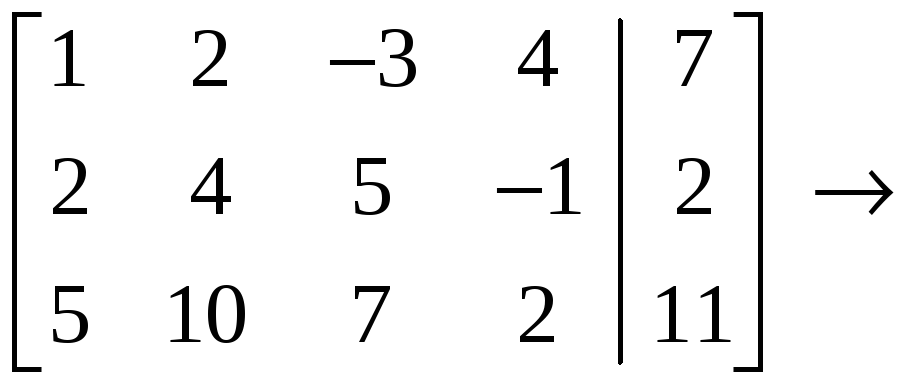
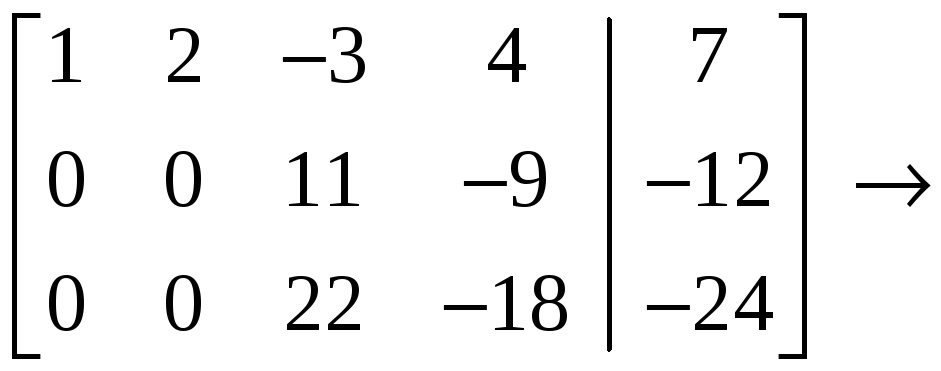
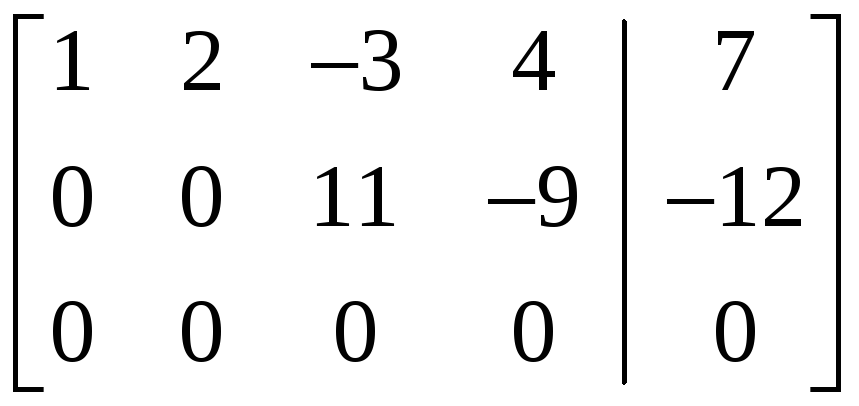Очевидно,
что
(система уравнений (20) совместна). Выберем
какой-нибудь не равный нулю минор второго
порядка полученной матрицы
,
например, минор
.
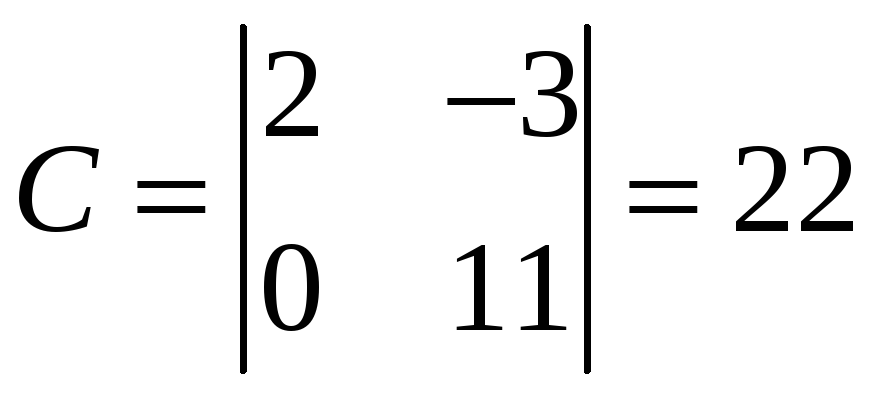Тогда
,
– базисные неизвестные,
и
– свободные неизвестные. Запишем систему
уравнений, которая является эквивалентной
исходной и соответствует полученной
расширенной матрице:
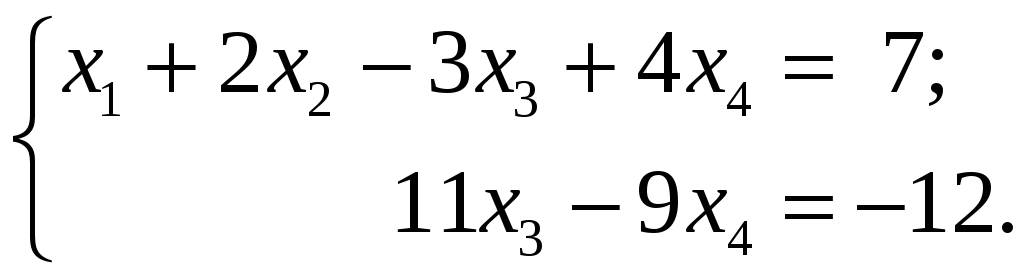
Выразим
из второго уравнения системы базисную
переменную
через свободную
и аналогичным образом из первого
уравнения найдём базисную переменную
как функцию свободных переменных
и
:
,
.
Теперь
пусть
,
,
где
.
Тогда общее решение исходной системы
уравнений имеет вид:
.
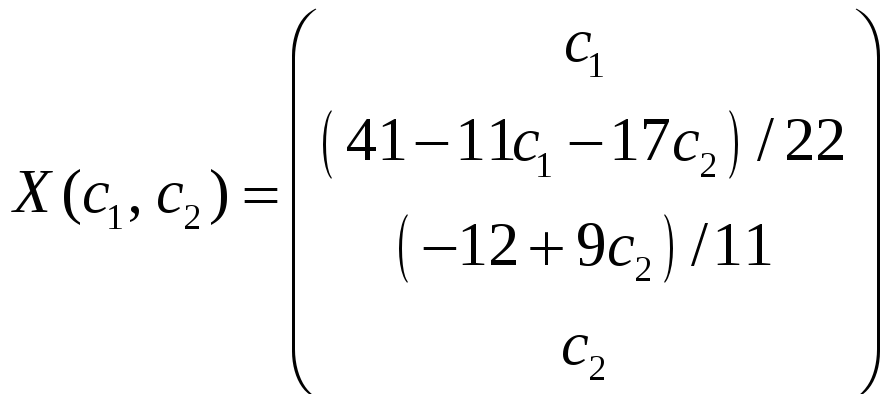4.2.2 Пример. Методом Гаусса исследовать совместность и найти общее решение системы
Решение.
С
помощью элементарных преобразований
строк расширенную матрицу
приведём к
виду
.
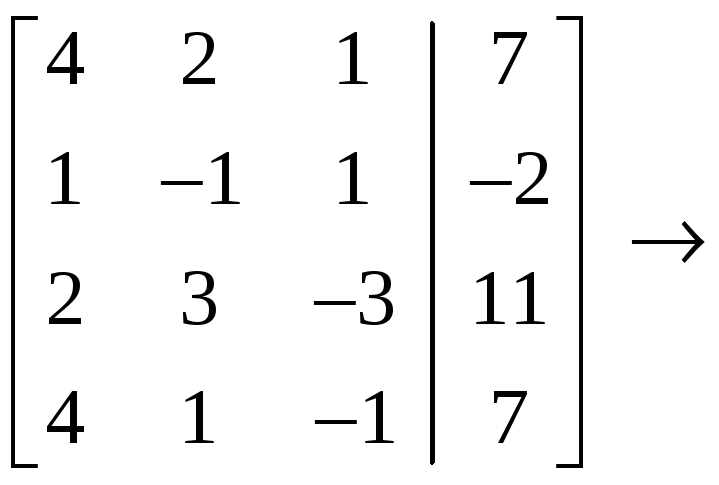
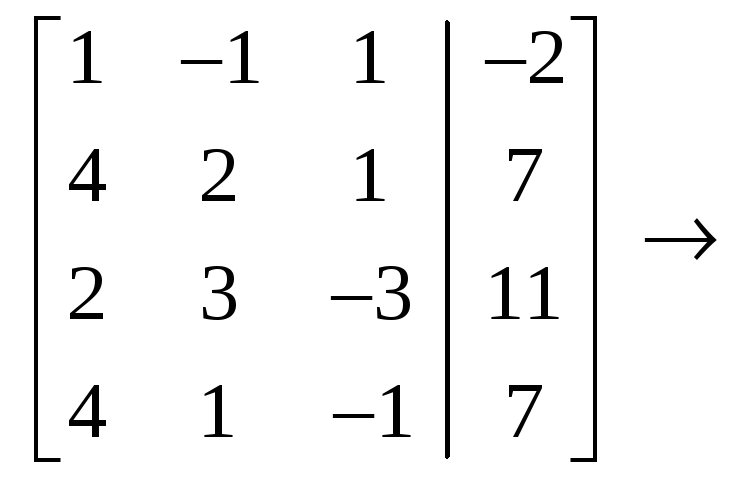
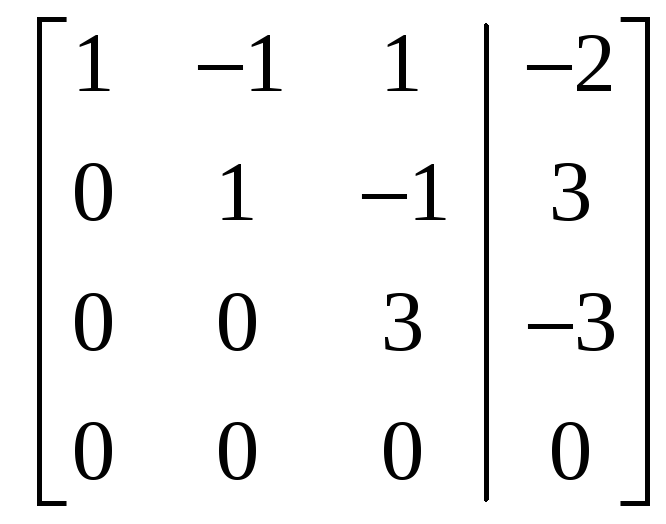Итак,
(система уравнений совместна и имеет
единственное решение, так как
).
Полученной
матрице соответствует система
которая
эквивалентна исходной. Из данной системы
следует, что
,
,
.
Итак, общее решение
.
4.3 Упражнения
4.3.1 Исследовать следующие системы уравнений и в случае совместности найти общее и одно частное решение:
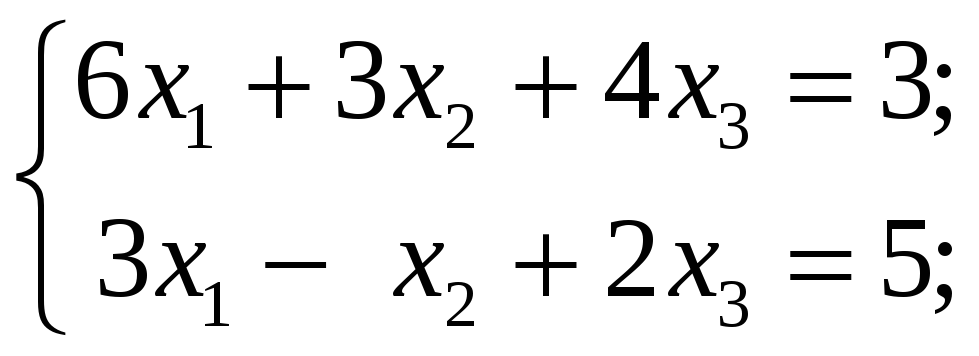
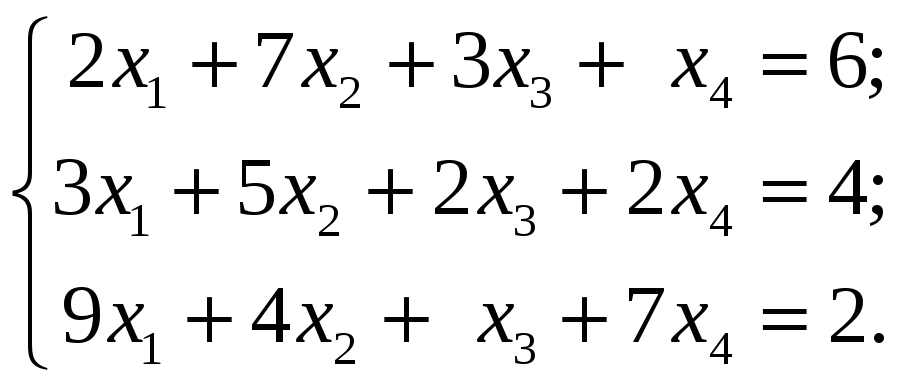
4.3.2 Методом Гаусса исследовать следующие системы уравнений и в случае совместности найти общее решение:
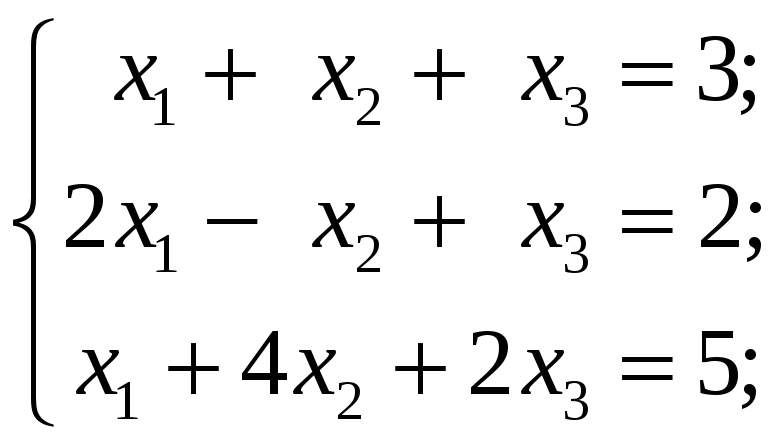
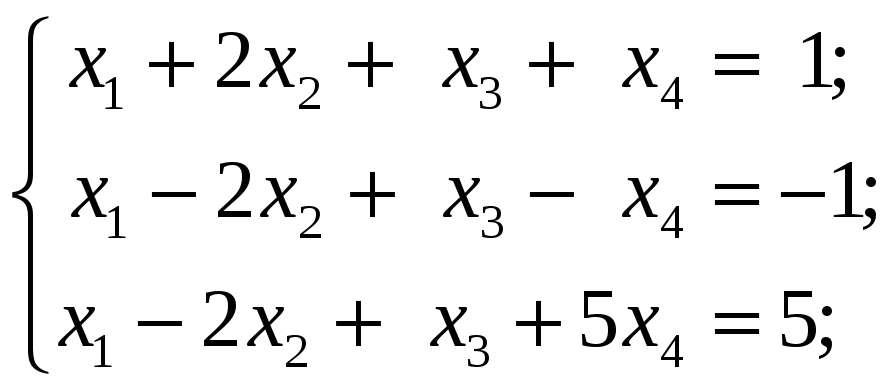
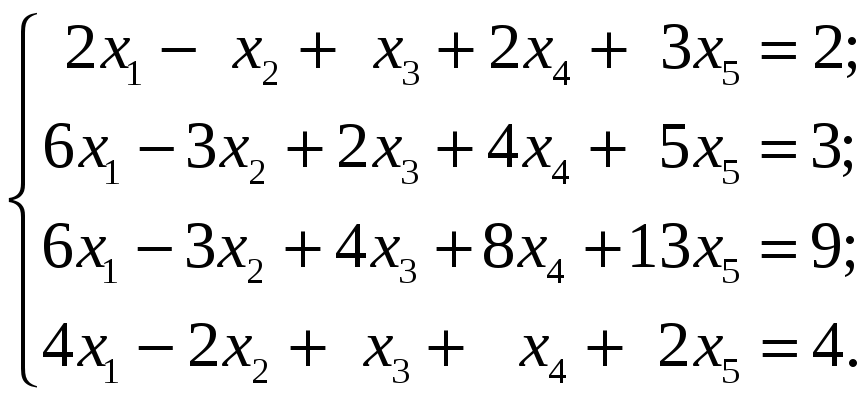
4.4 Контрольные задания
Рекомендуемая литература [1, гл. 5, § 4], [2, гл. 1, § 1.11, § 1.16 – 1.17], [3, гл. 3, § 3.4, § 3.7].
4.4.1 Исследовать следующие системы уравнений и в случае совместности найти общее решение:
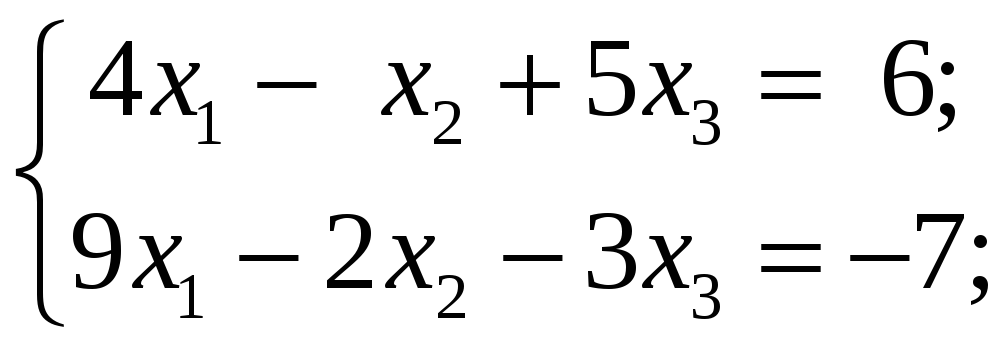
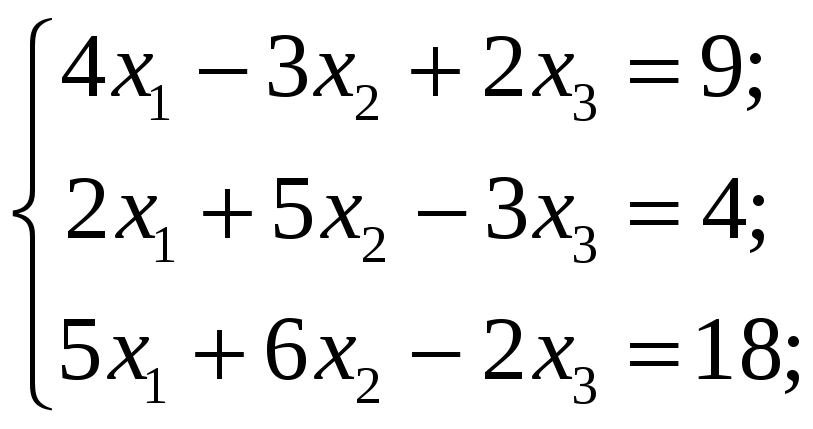
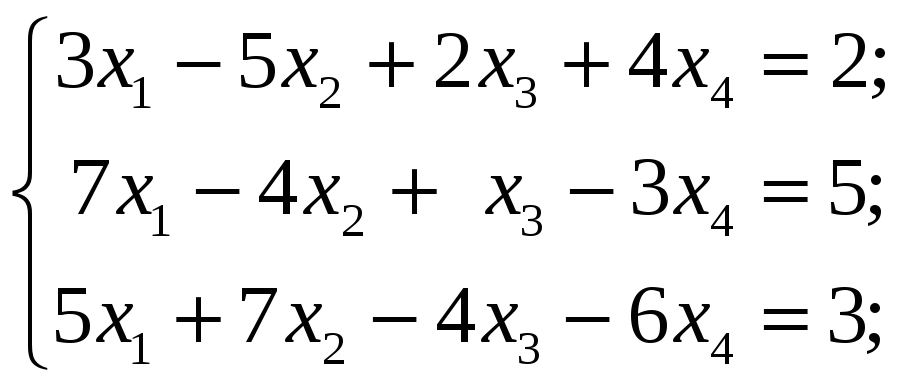
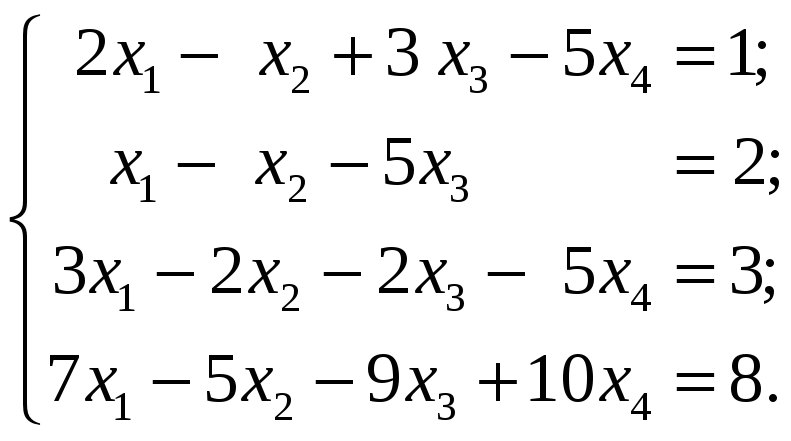
5 Однородные и неоднородные системы линейных уравнений
Цель занятия: выработка навыков построения фундаментальной системы решений и общих решений однородной и неоднородной систем уравнений.
5.1 Структура общего решения однородных и неоднородных систем
5.1.1
Определение.
Если в (17)
,
то система уравнений называется
однородной и имеет вид:
(23)
Система
(23) всегда совместна, т. к. она имеет
нулевое (тривиальное) решение
.
Приведём условия, при которых система
(23) имеет ненулевые решения.
5.1.2 Теорема. Для того чтобы система (23) имела ненулевые решения, необходимо и достаточно, чтобы ранг её основной матрицы был меньше числа неизвестных.
Отсюда
следует, что если
,
то нулевое решение будет единственным
решением системы (23). Если же
,
то система (23) в соответствии с (п. 4.1.2.4)
имеет бесконечно много решений.
Предположим, что
и
– базисные неизвестные системы (23),
– свободные неизвестные. Тогда общее
решение системы (23) будет иметь вид (19).
Выберем
решений (23), полученных из общего решения
так: одно из значений свободных переменных
полагаем равным 1, а остальные – равными
0:
,
,
…,
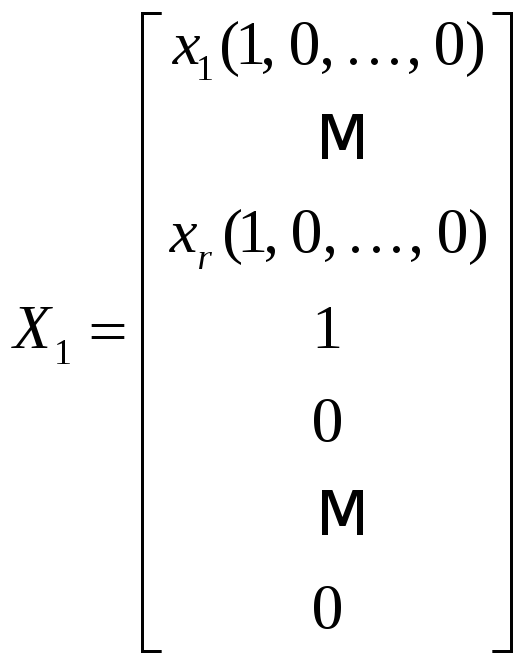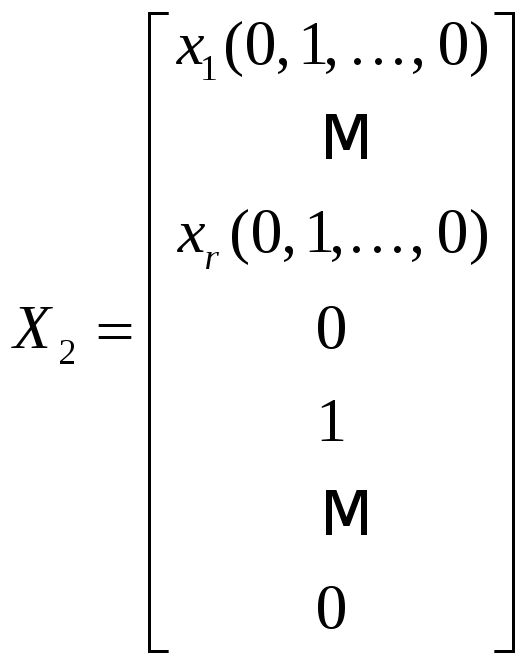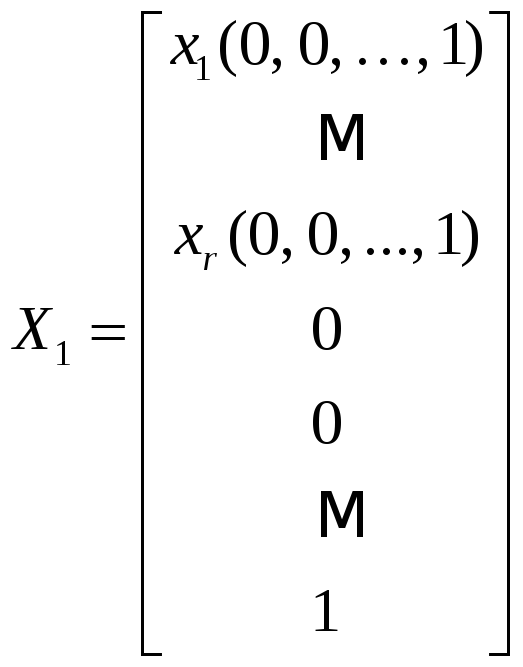. (24)
Эти решения образуют систему решений однородной системы (23), обладающую следующим свойством: произвольное решение системы (23) может быть единственным образом представлено в виде
, (25)
где
некоторые числа.
5.1.3
Определение.
Любой набор из
решений однородной системы (23), обладающих
указанным свойством, называется
фундаментальной системой решений
системы (23).
Формула (25) определяет структуру общего решения однородной системы (23).
5.1.4
Определение.
Если в (17) среди свободных членов
(
)
хотя бы один отличен от нуля, то система
уравнений называется неоднородной.
Структура общего решения неоднородной системы уравнений определяется следующей теоремой.
5.1.5 Теорема. Общее решение неоднородной системы может быть представлено в виде
, (26)
где
– частное решение неоднородной системы
уравнений,
– общее
решение соответствующей однородной
системы.
5.1.6 Пример. Найти общее решение и фундаментальную систему решений однородной системы линейных уравнений:
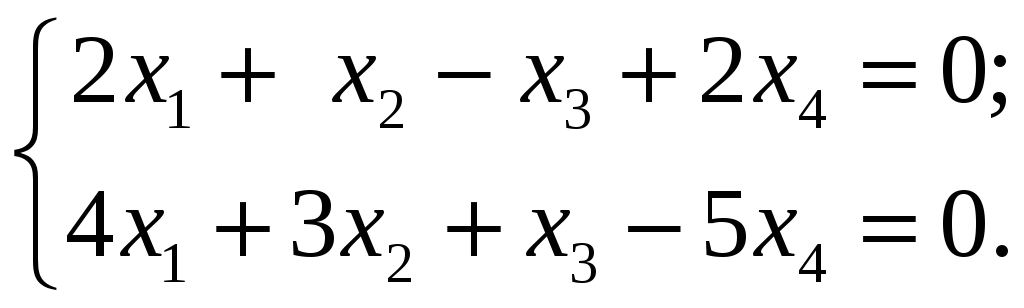
Решение.
Имеем
,
.
В качестве
базисного минора возьмём
.
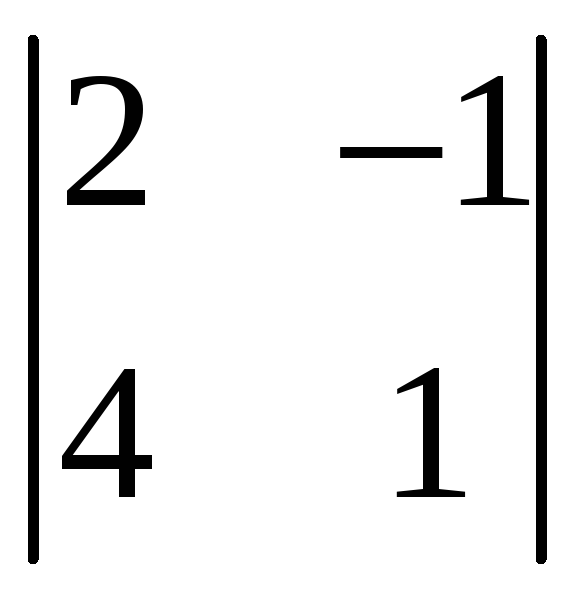Наша система эквивалентна следующей:
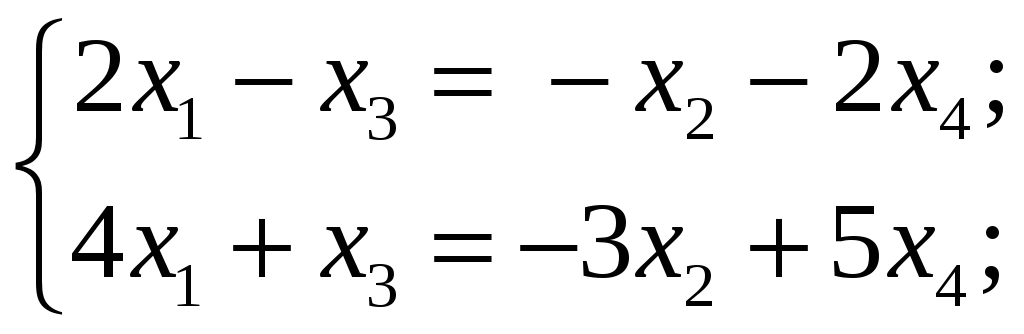
где
,
– базисные
неизвестные;
,
– свободные неизвестные.
Откуда
;
.
Теперь
пусть
,
,
где
.
Тогда общее решение исходной системы
уравнений имеет вид:
.
Из общего решения находим фундаментальную систему решений:
,
.
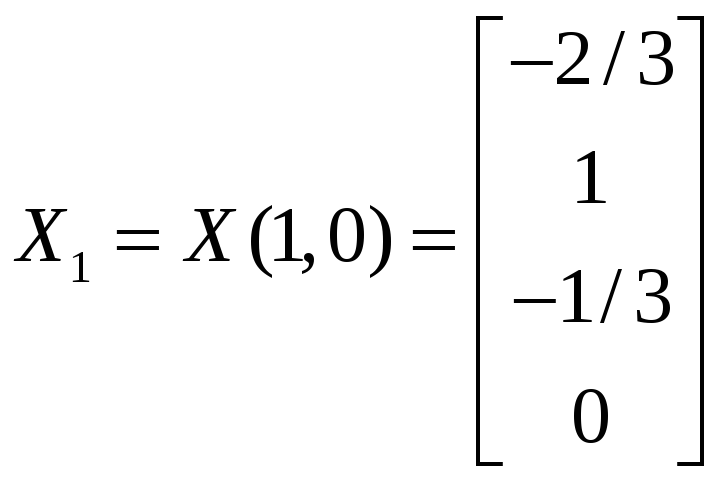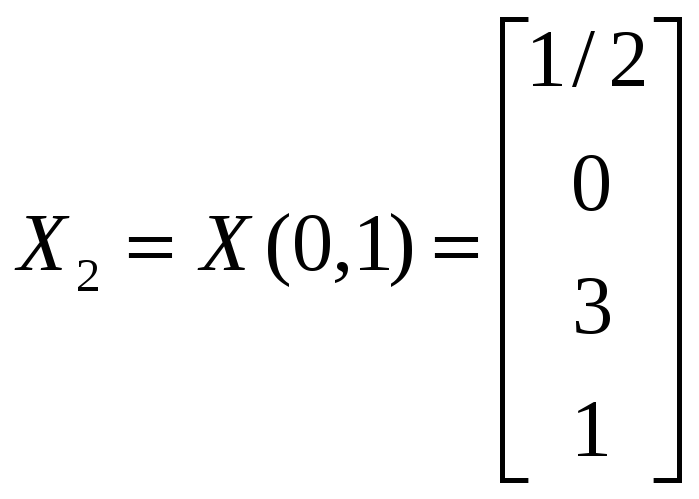С
использованием фундаментальной системы
общее решение может быть записано в
виде
.
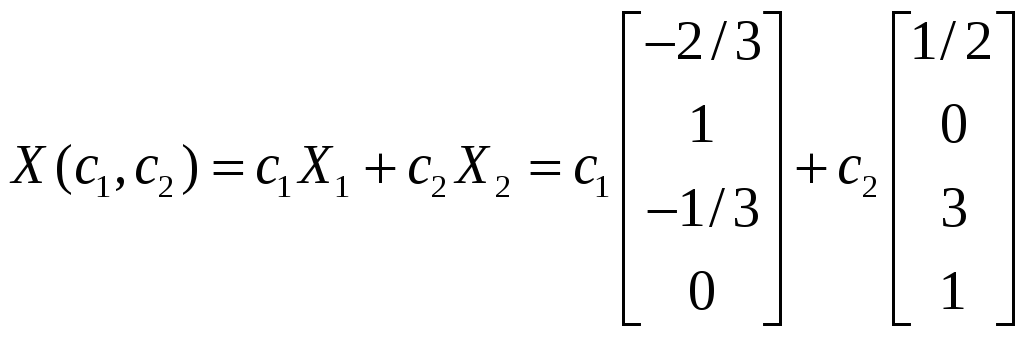5.1.7 Пример. Найти общее решение неоднородной системы уравнений, используя фундаментальную систему решений соответствующей однородной:
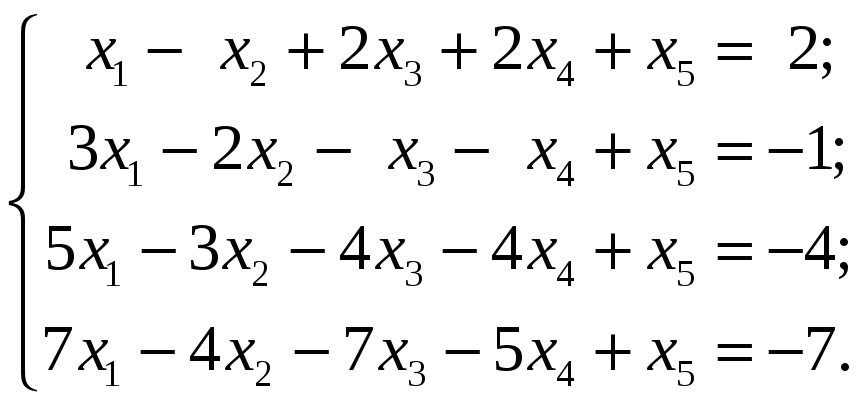
Решение.
С
помощью элементарных преобразований
строк расширенную матрицу
приведём к
виду
.
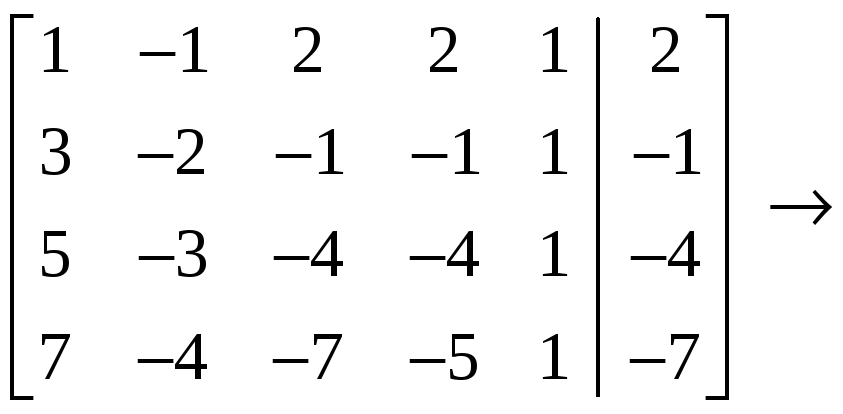
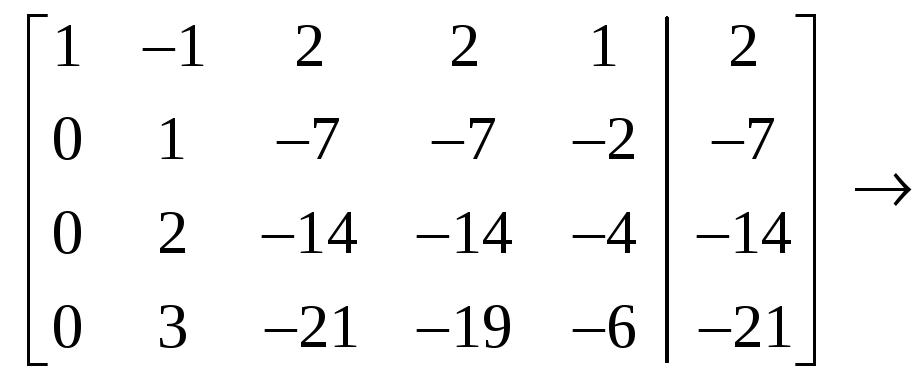
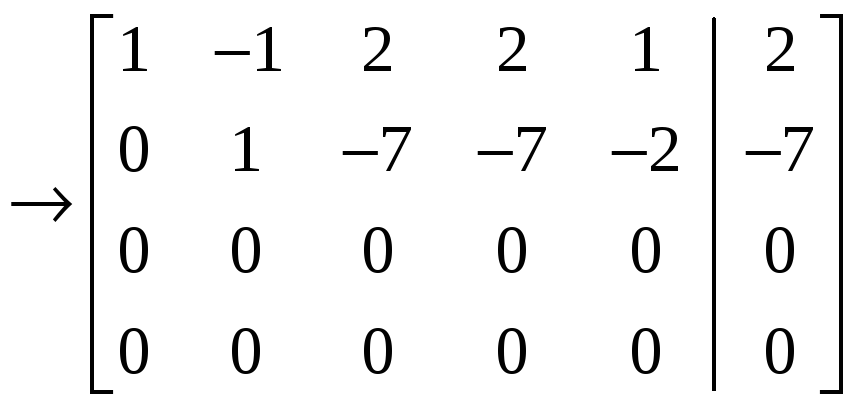Имеем
,
.
В качестве базисного минора возьмём
.
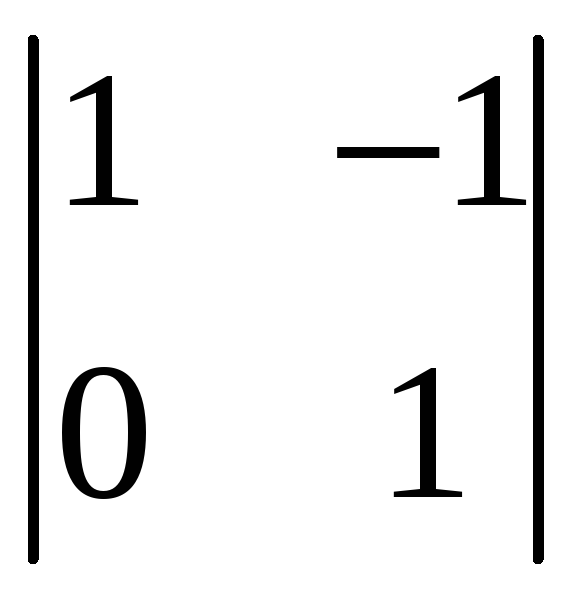Наша система эквивалентна следующей:
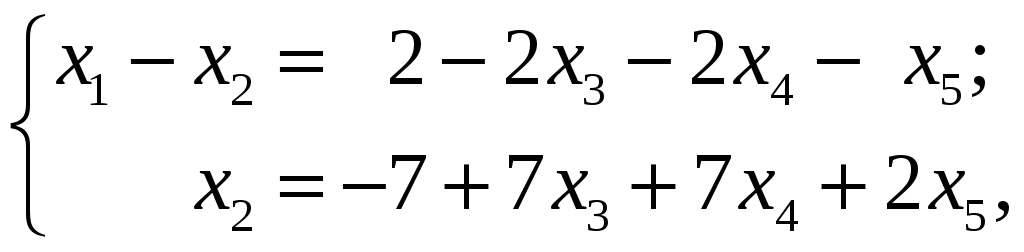
где
– базисные
неизвестные;
– свободные
неизвестные.
Откуда
;
.
Теперь
пусть
,
где
.
Тогда общее решение исходной системы
уравнений имеет вид:
,
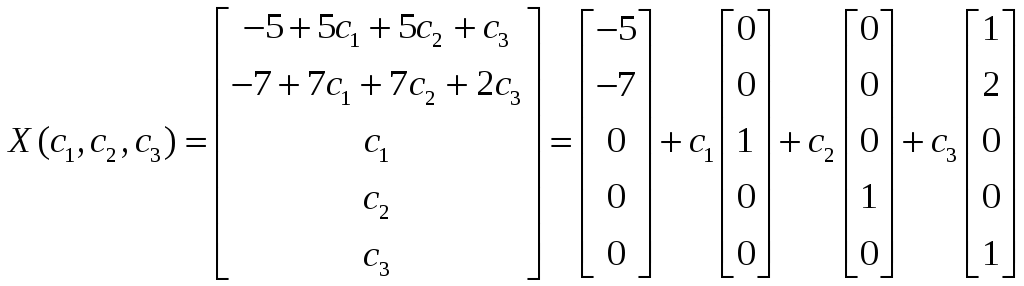т. е.
,
где
– частное решение, а столбцы
,
,
образуют фундаментальную систему
решений соответствующей однородной
системы.