1.3 Упражнения
1.3.1
Найти
,
если
,
.
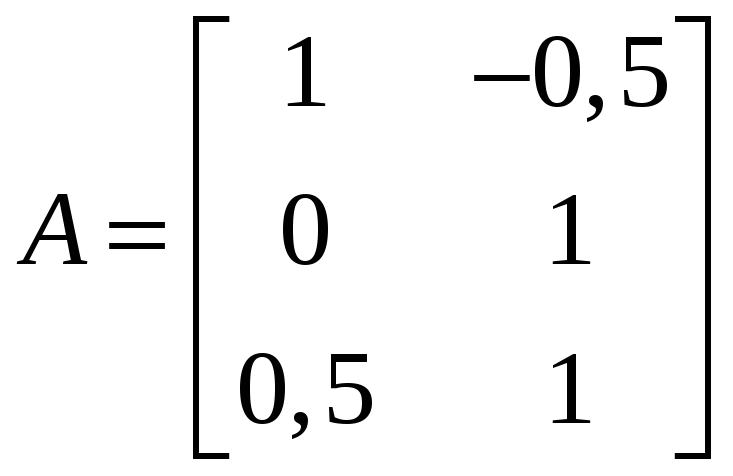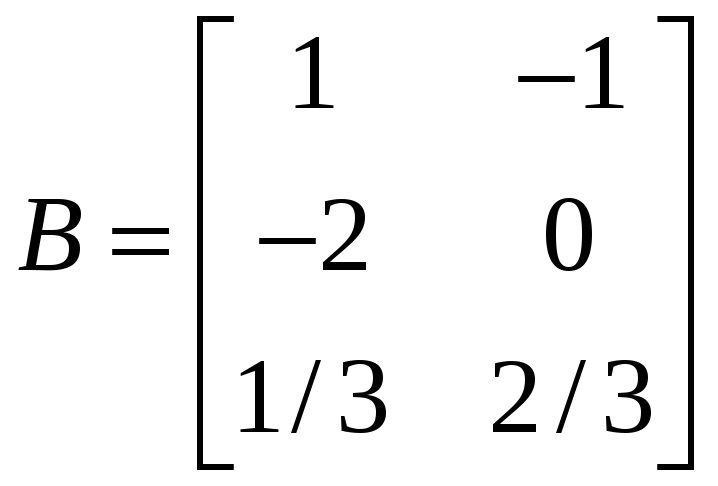1.3.2
Найти
,
если
,
.
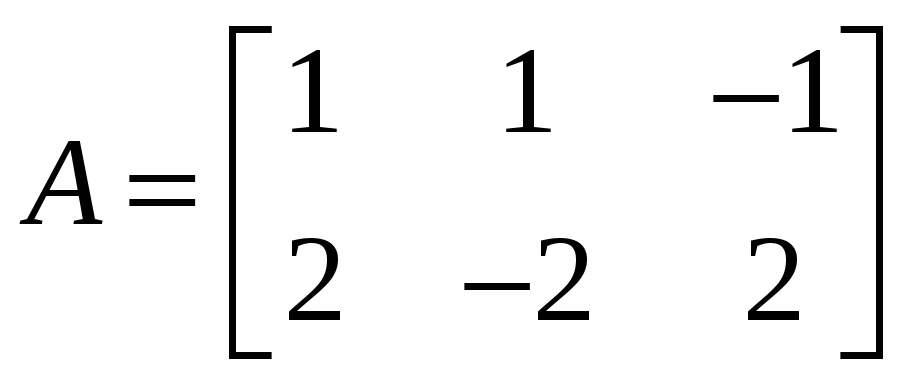1.3.3 Вычислить
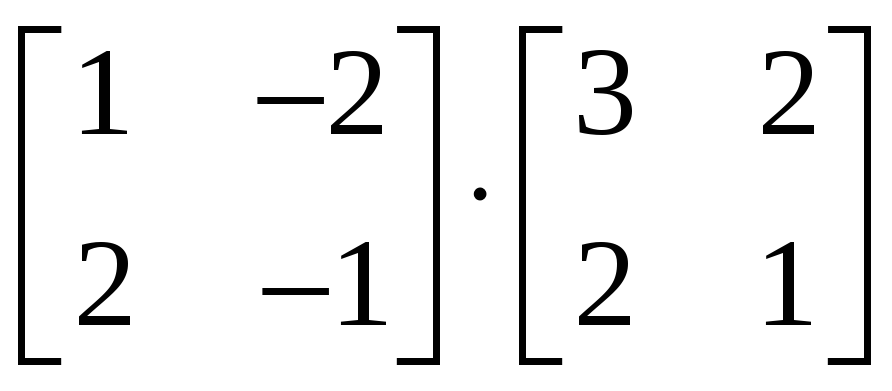и
.
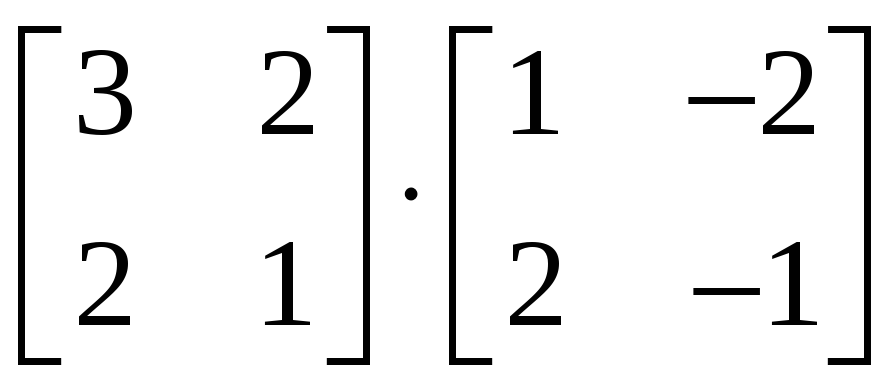1.3.4 Вычислить
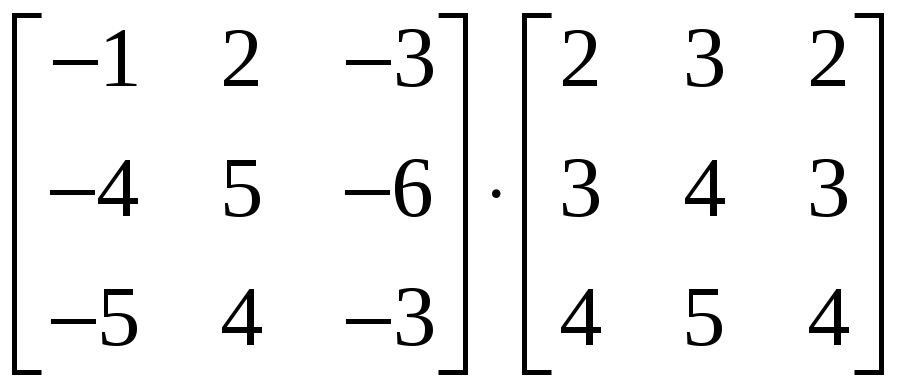и
.
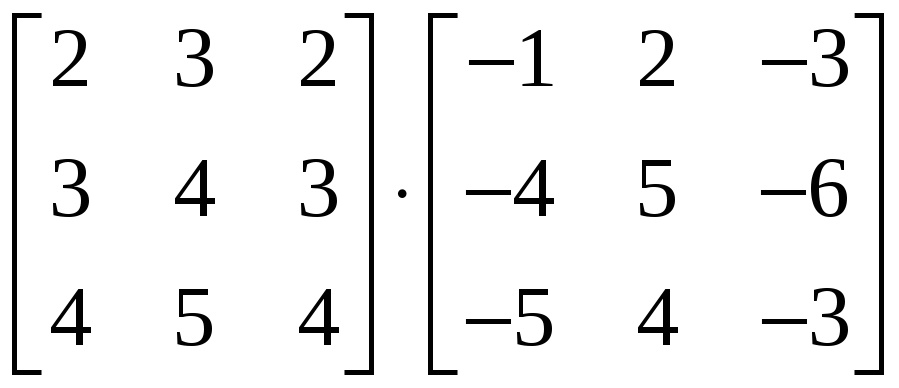1.3.5 Вычислить
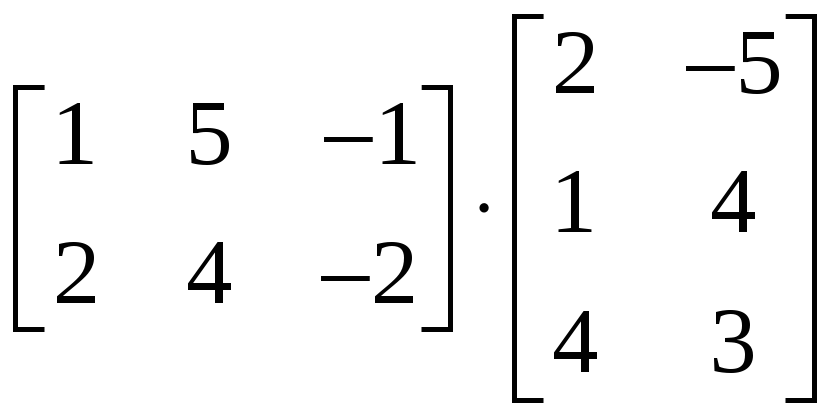и
.
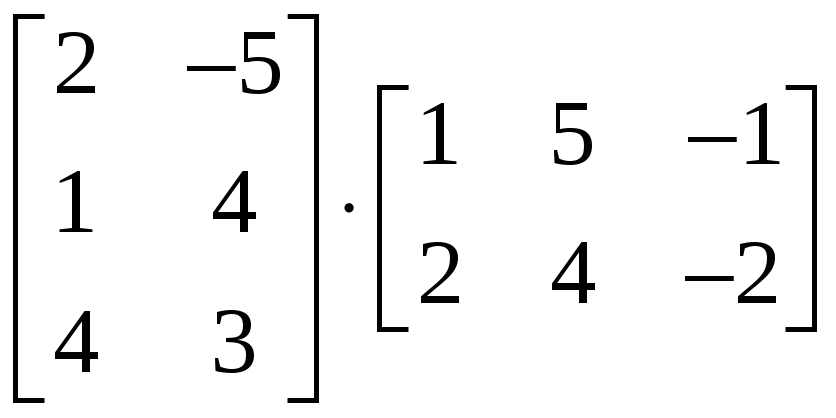1.3.6
Вычислить
,
если
.
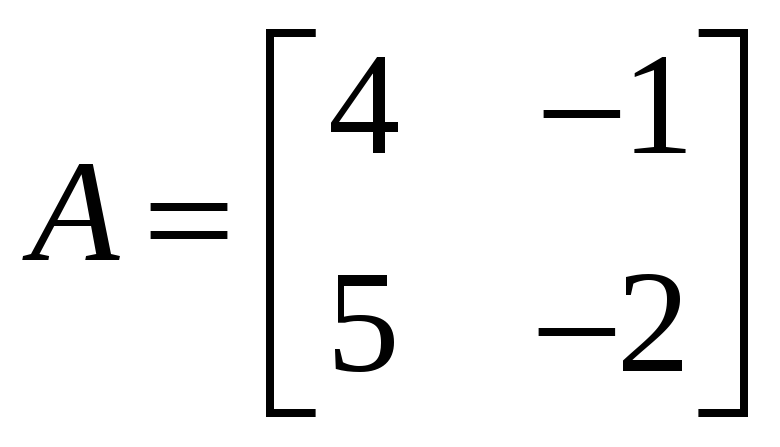1.3.7
Найти
,
если:
,
.
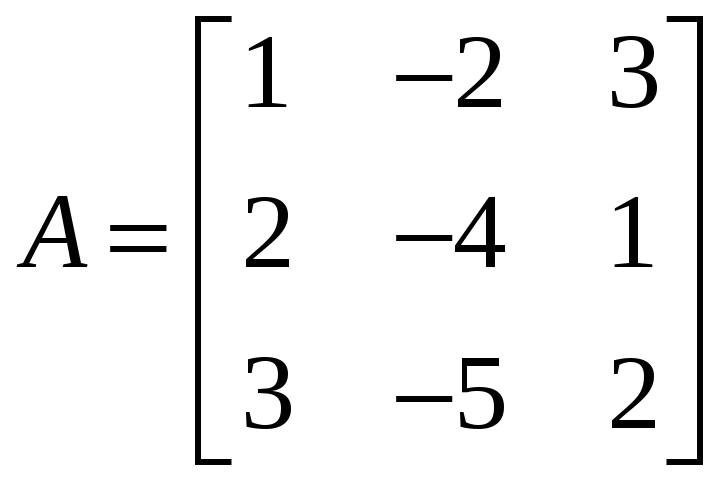1.3.8 Вычислить следующие определители:
,
,
,
,
,
,
,
,
,
,
.
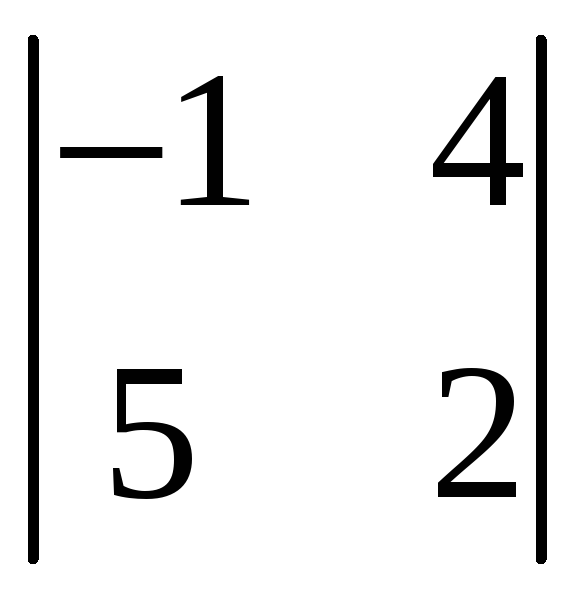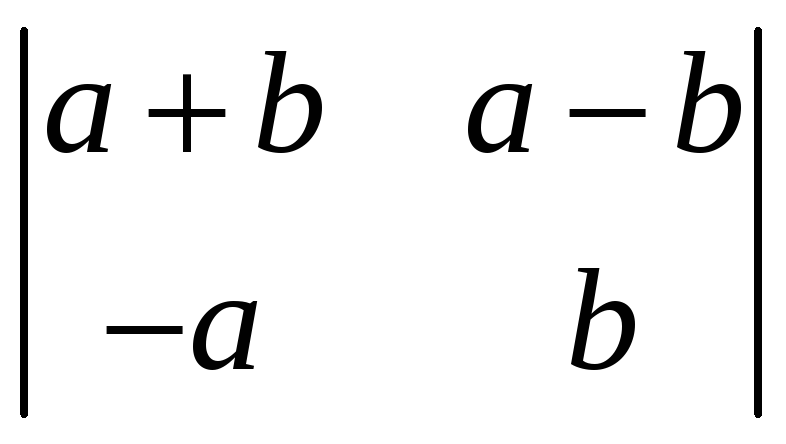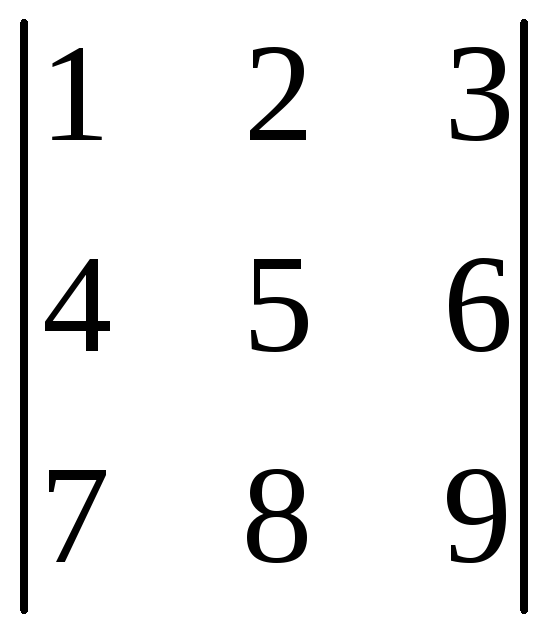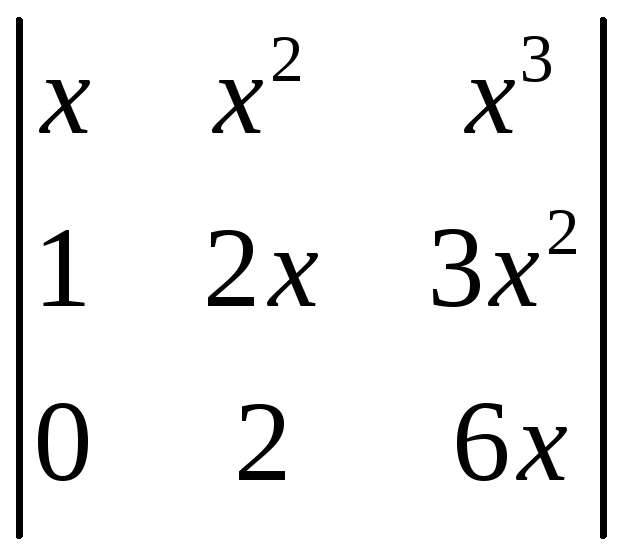1.3.9 Решить уравнения:
,
,
,
.
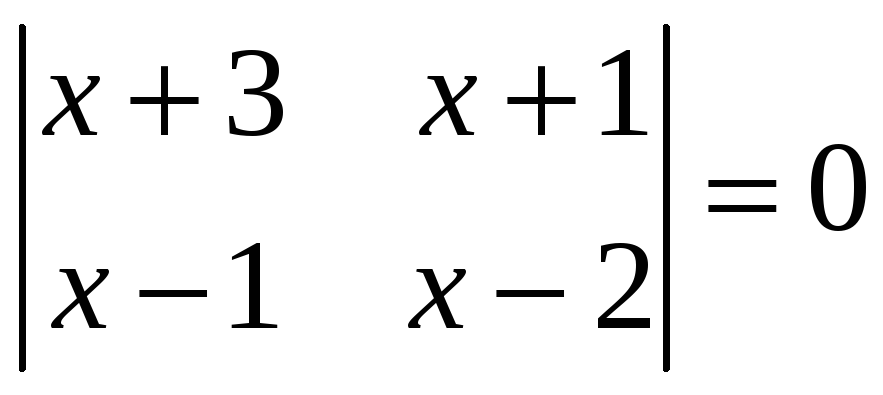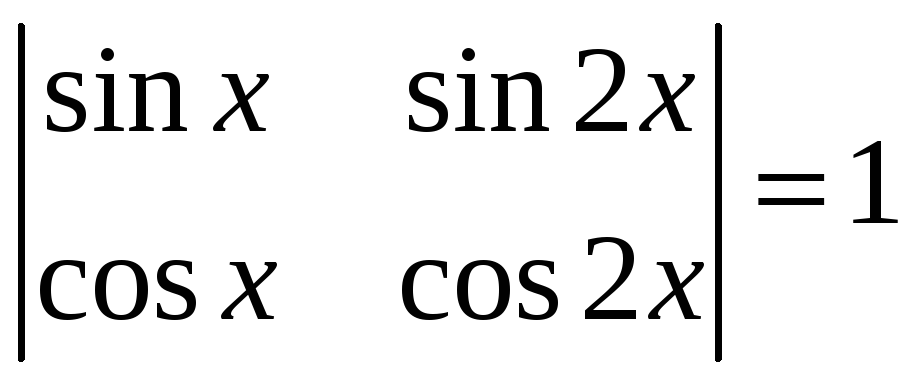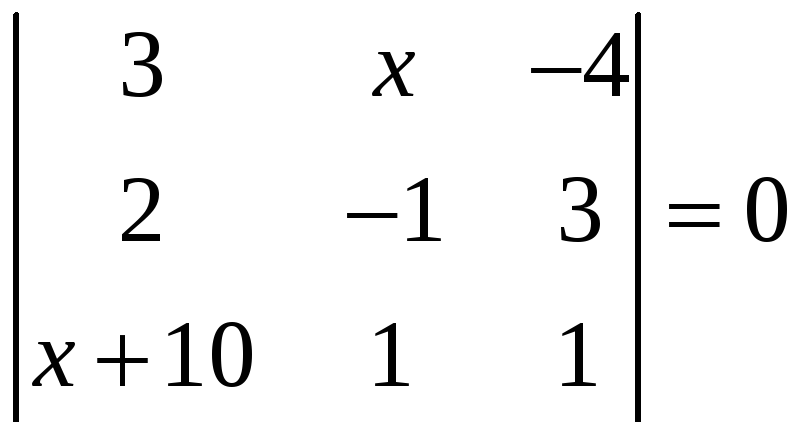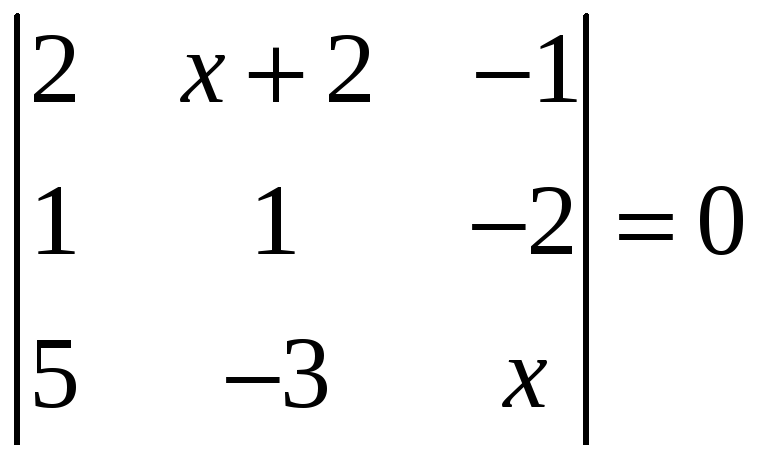1.4 Контрольные задания
Рекомендуемая литература [1, гл. 1, § 1], [2, гл. 2, § 1.6, § 1.13], [3, гл. 3, § 3.1, § 3.2].
1.4.1 Вычислить
.
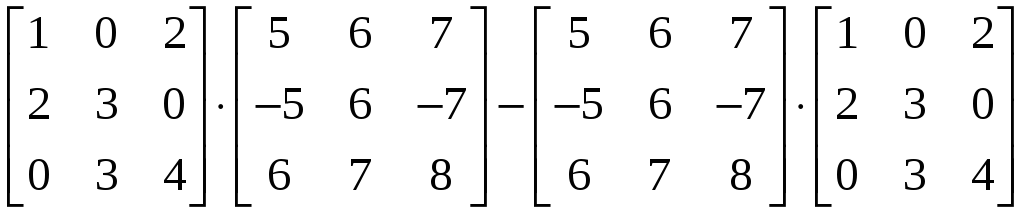1.4.2
Вычислить
,
если:
,
,
.
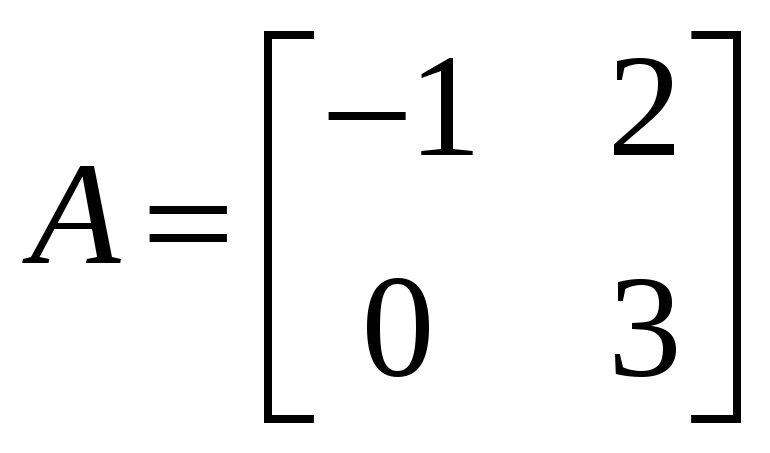1.4.3 Решить уравнения:
,
,
,
.
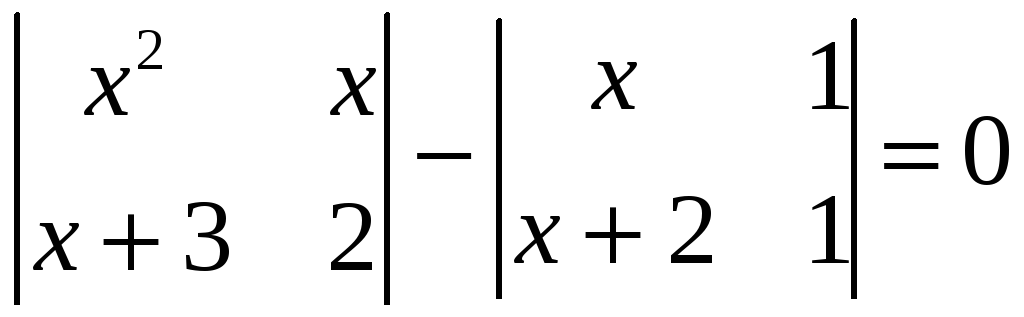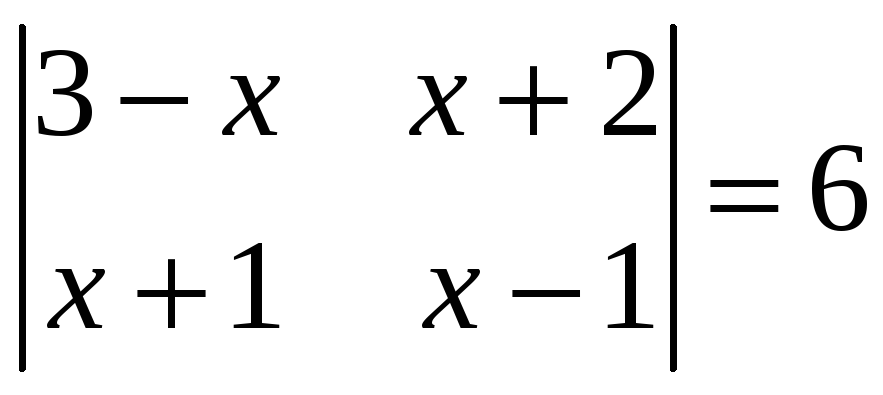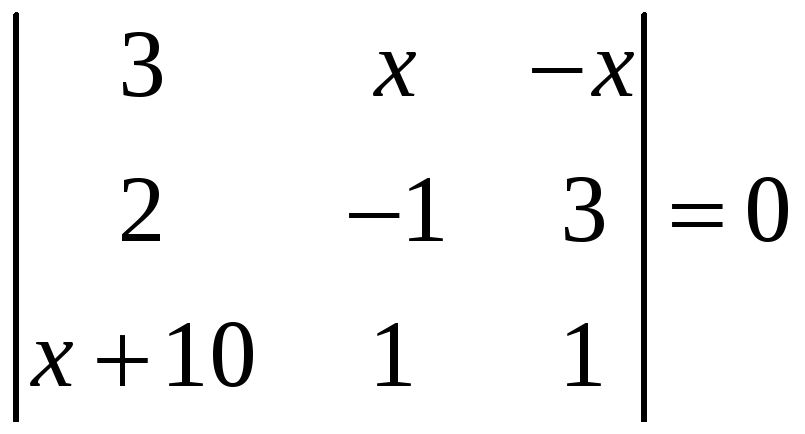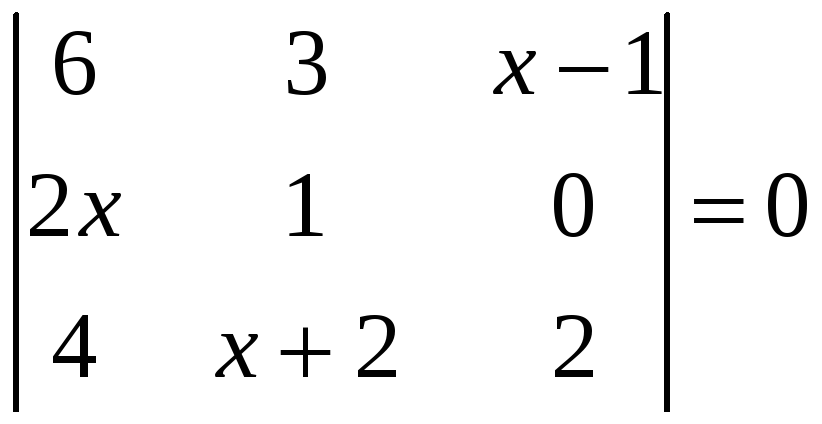1.4.4 Вычислить следующие определители:
,
,
,
,
,
.
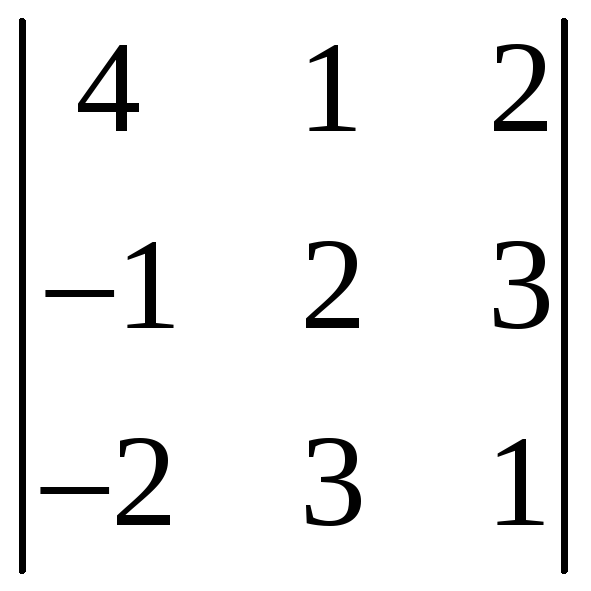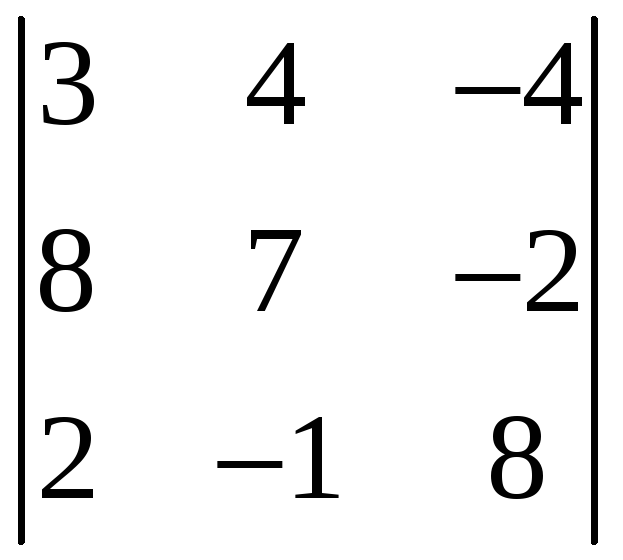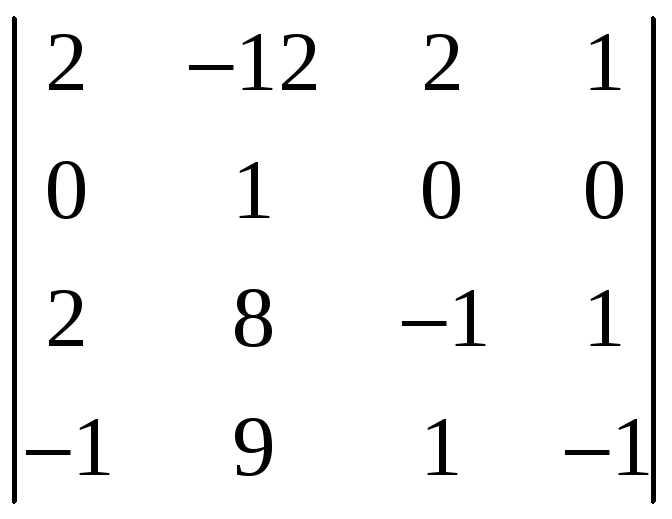2 Обратная матрица. Ранг матрицы
Цель занятия: усвоение понятий обратной матрицы и ранга матрицы, выработка навыков построения обратной матрицы и вычисления ранга матрицы.
2.1 Обратная матрица
Квадратная
матрица
называется невырожденной, если
и вырожденной, если
.
2.1.1
Определение.
Пусть
– матрица порядка
.
Матрица
называется
обратной для
,
если
,
где
– единичная матрица порядка
.
2.1.2
Теорема.
Матрица
имеет обратную матрицу
тогда и только тогда, когда она невырождена.
Обратная матрица
для матрицы
,
,
имеет следующий вид:
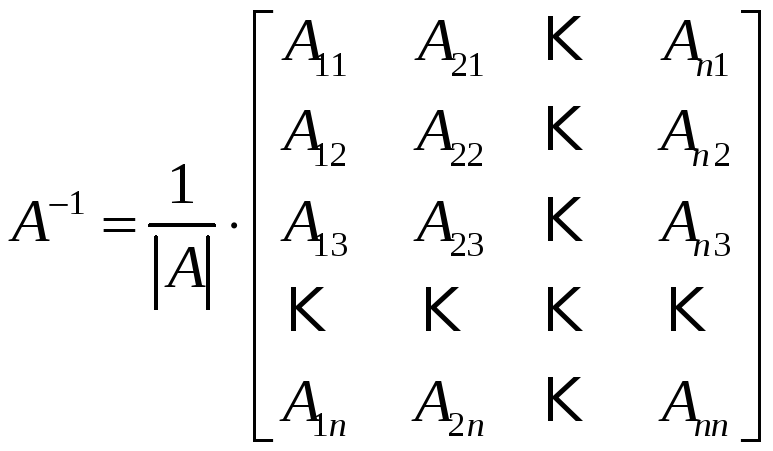, (10)
где
– алгебраические дополнения элементов
матрицы
.
Матрицу, стоящую в правой части выражения (10), называют присоединённой матрицей. В применении выражения (10) состоит метод присоединённой матрицы вычисления обратной матрицы.
Кроме того, для вычисления обратной матрицы используется метод элементарных преобразований.
2.1.3 Определение. Элементарными преобразованиями матрицы называются следующие:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число, отличное от нуля;
3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.
Суть
метода элементарных преобразований
состоит в следующем. Приписывая справа
к данной матрице
размера
единичную матрицу размера
,
получают прямоугольную матрицу
размера
.
Далее, используя элементарные
преобразования над строками, приводят
матрицу
к виду
:
.
2.1.4
Пример.
Методом присоединённой матрицы найти
обратную маирицу для данной матрицы
.
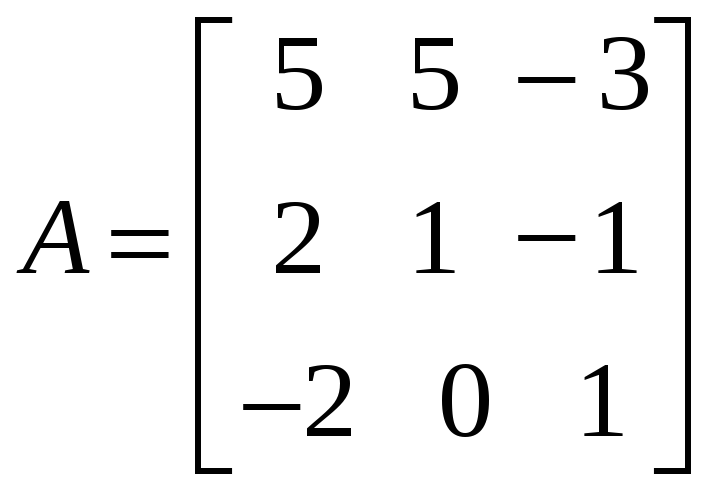Решение.
Имеем:
,
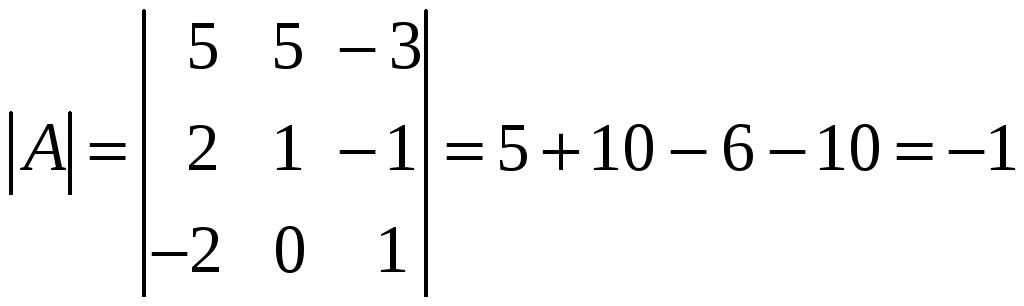значит
невырождена и матрица
существует. Находим алгебраические
дополнения ко всем элементам матрицы
:
;
;
;
;
;
;
;
;
.
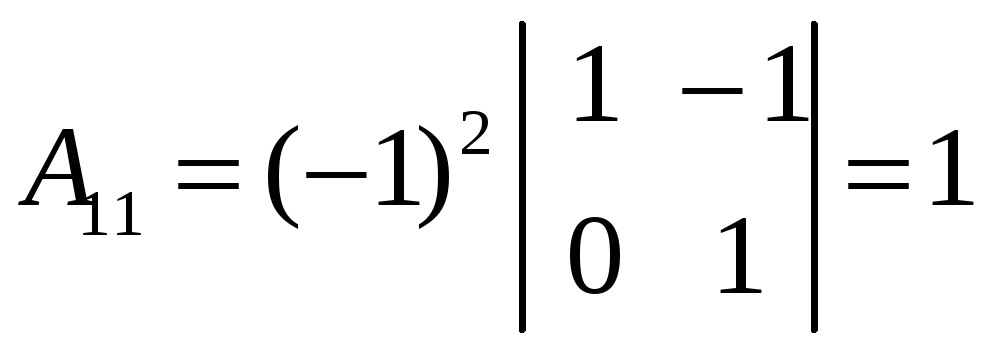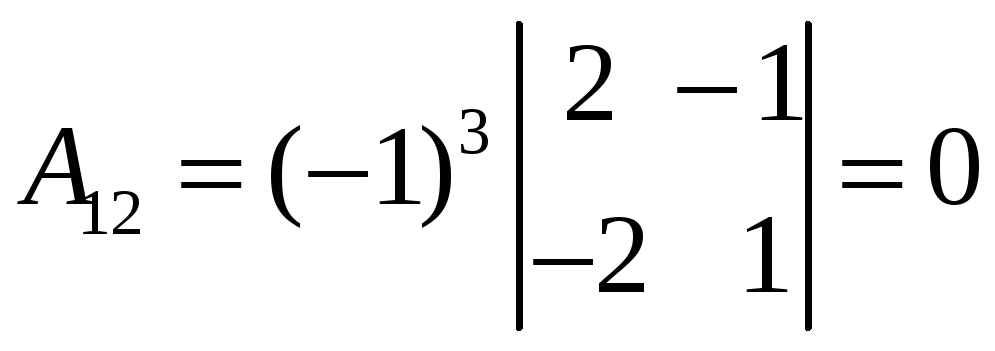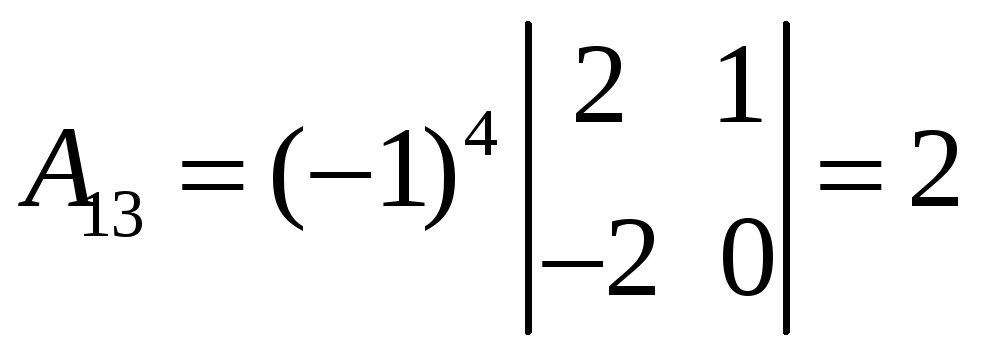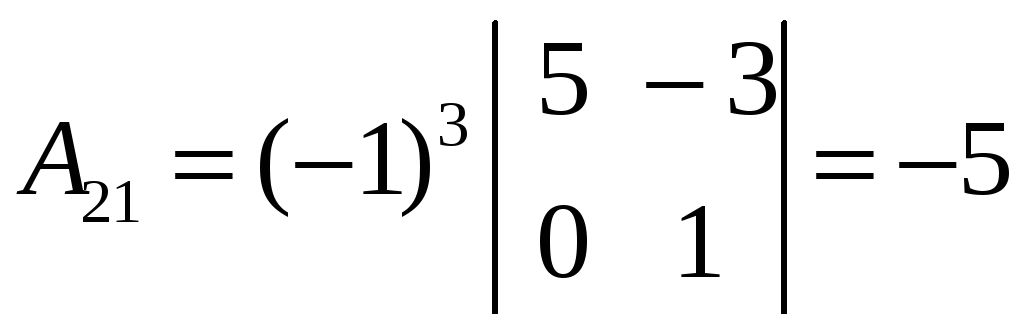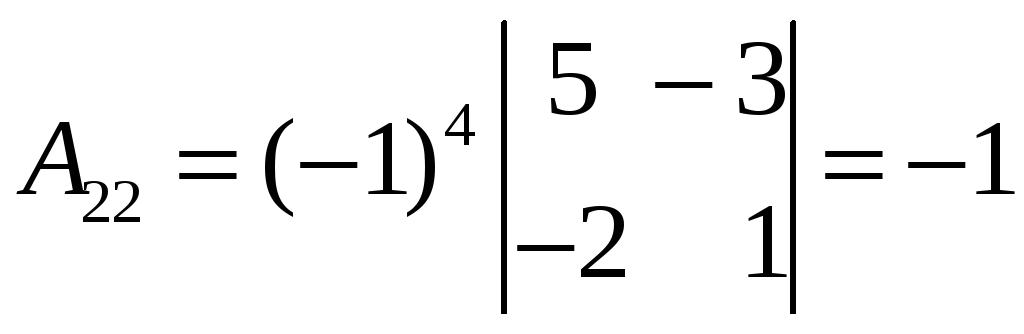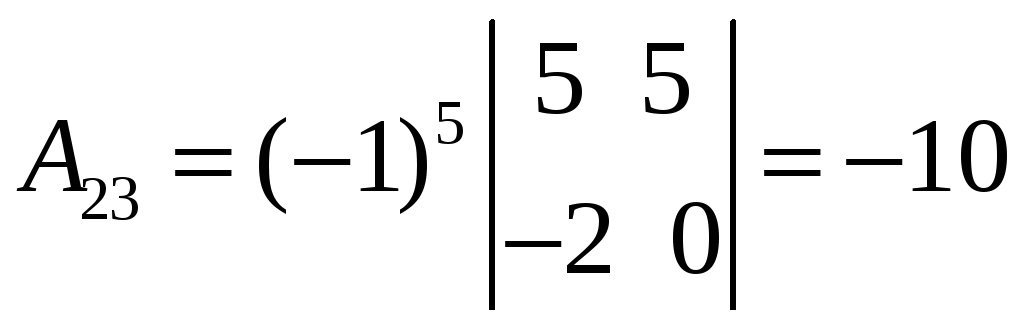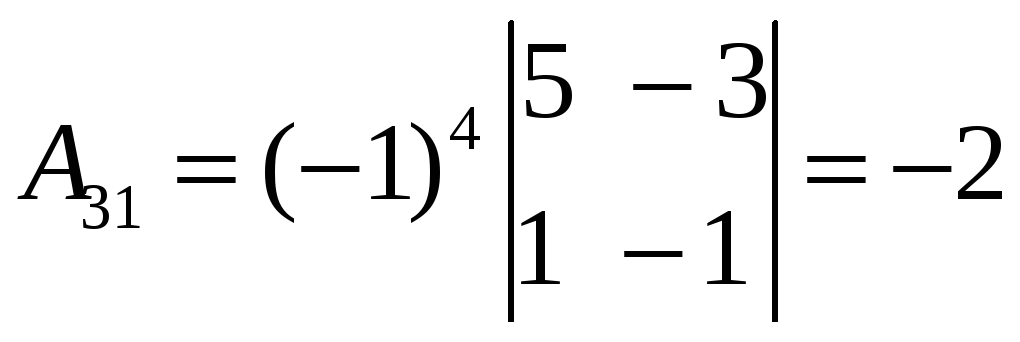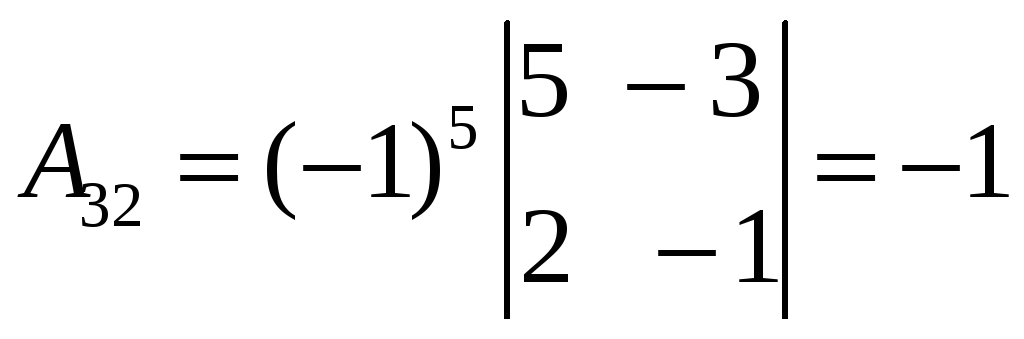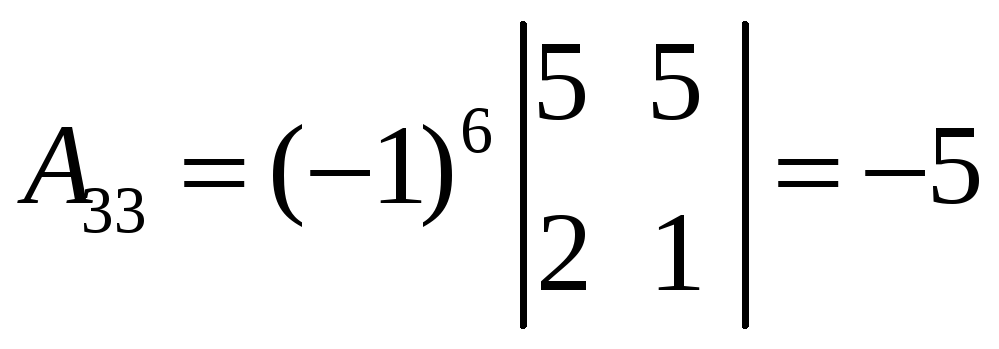Итак,
.
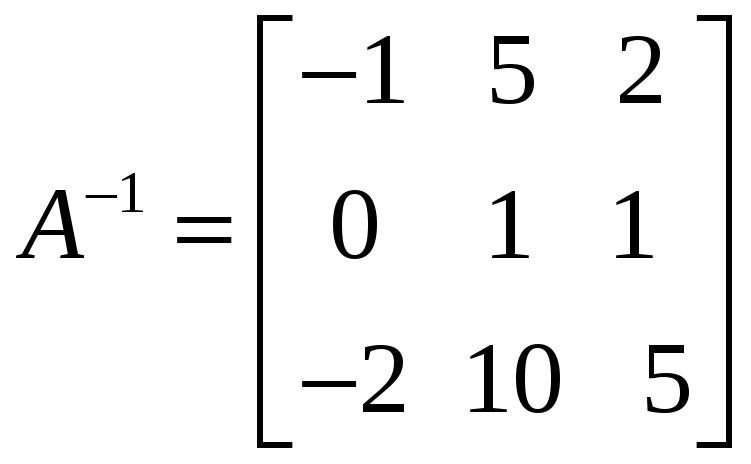2.1.5
Пример.
Методом элементарных преобразований
найти обратную для данной матрицы
.
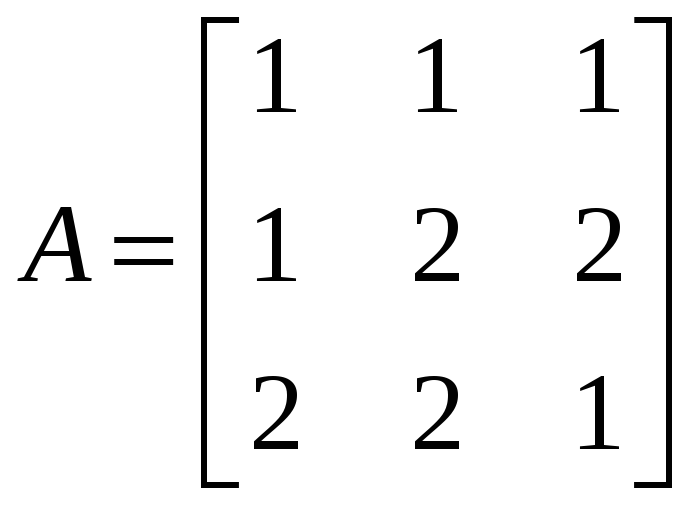Решение.
Составляем
матрицу
размера
и преобразуем её, приведём к виду
:
,
.
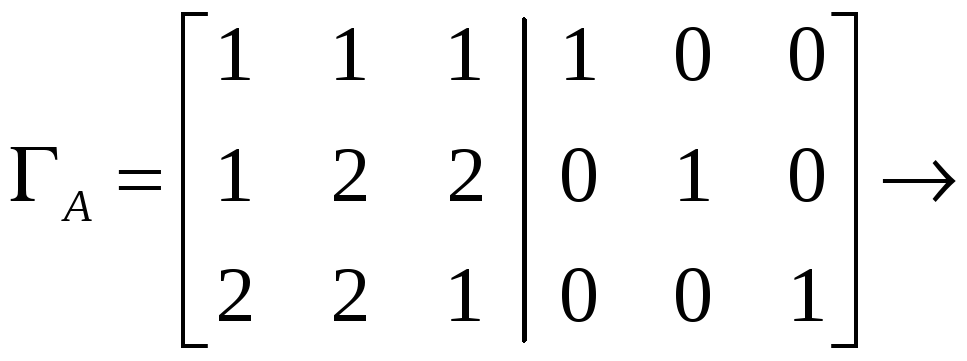
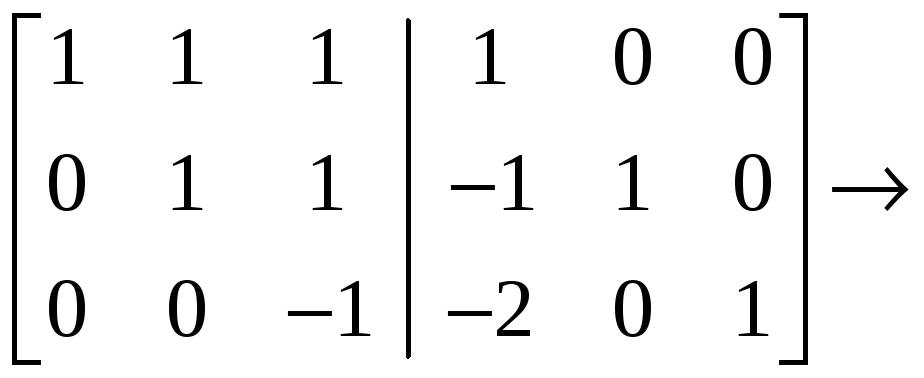
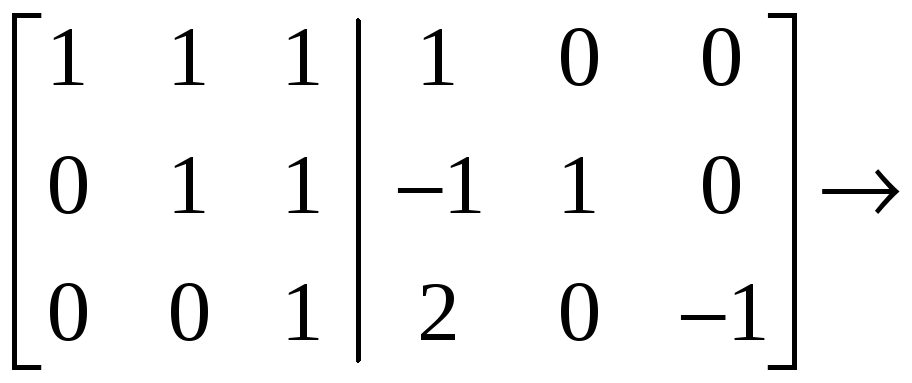
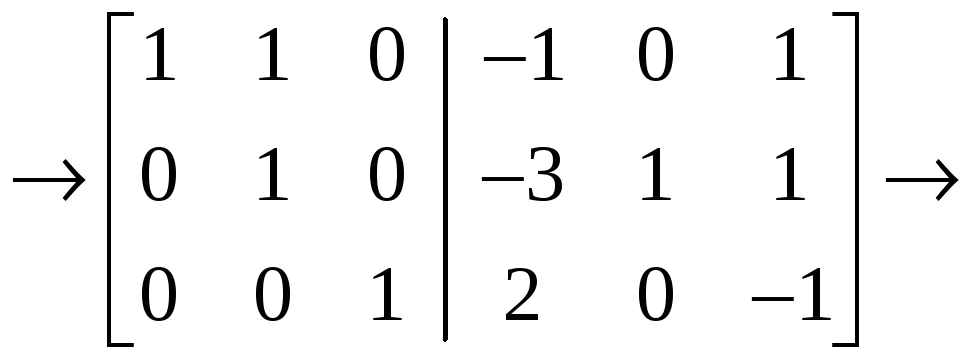
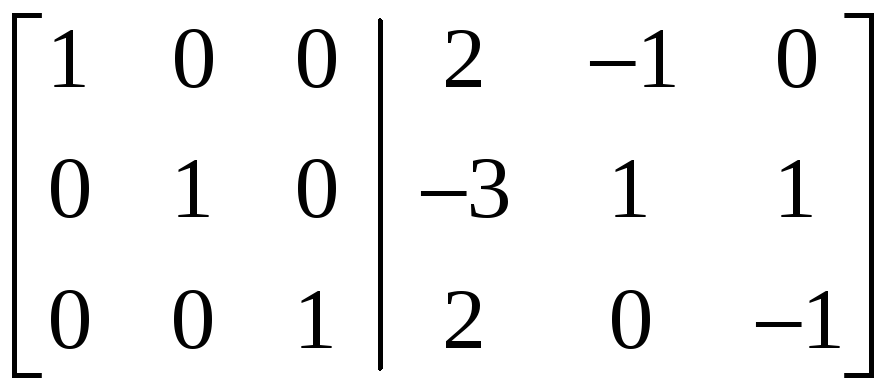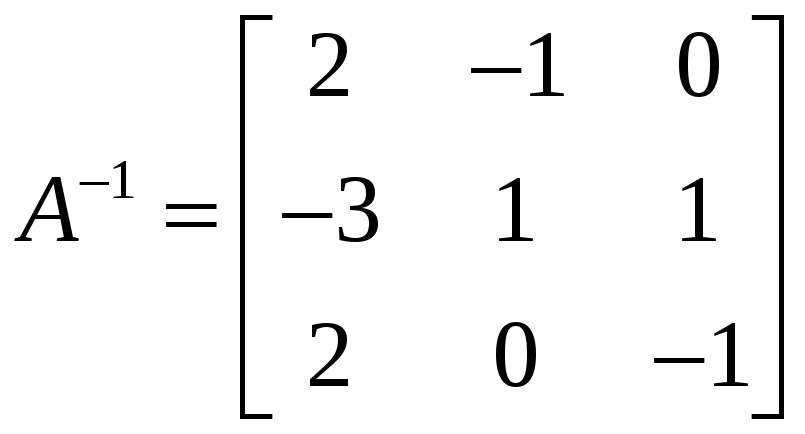Вторая
матрица получена из первой в результате
следующих элементарных преобразований:
элементы первой строки умножены на (
)
и сложены с элементами второй строки,
элементы первой строки умножены на (
)
и сложены с элементами третьей строки.
Умножив последнюю строку второй матрицы
на (
),
получим третью матрицу. Умножая третью
строку на (
)
и прибавляя её ко второй, а затем к первой
строке, получаем четвёртую матрицу.
Умножая её вторую строку на (
)
и прибавляя к первой строке, получаем
пятую матрицу: слева от черты − единичная
матрица, справа − матрица
,
обратная исходной матрице
.