2.3 Упражнения

2.3.1 Методом присоединённой матрицы найти обратные матрицы для следующих матриц:

, , , , ,

, , , .

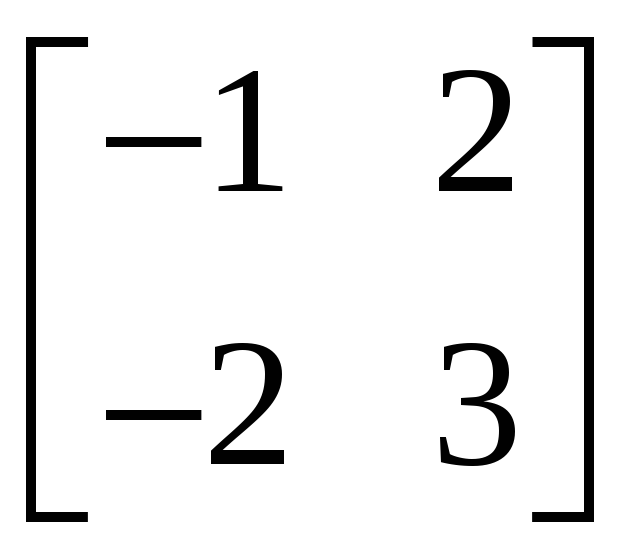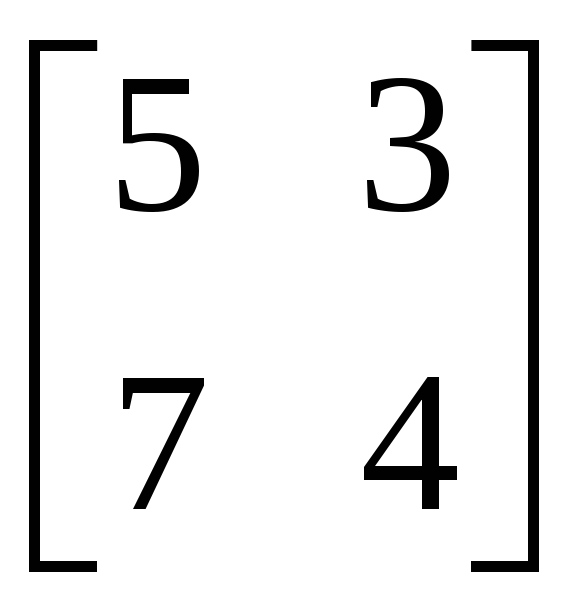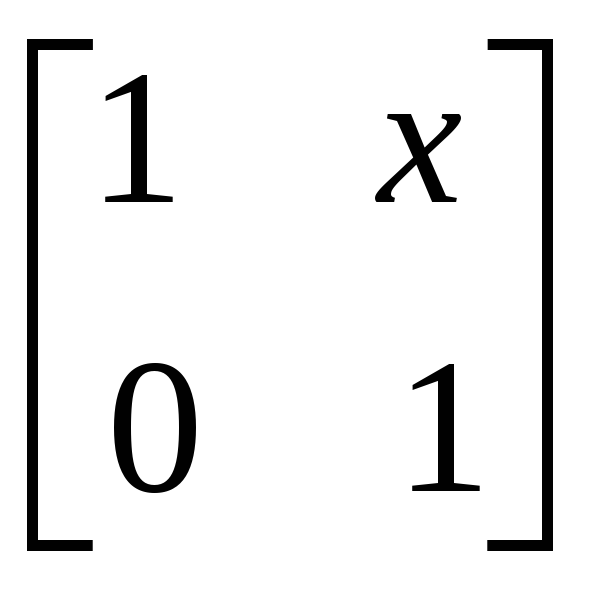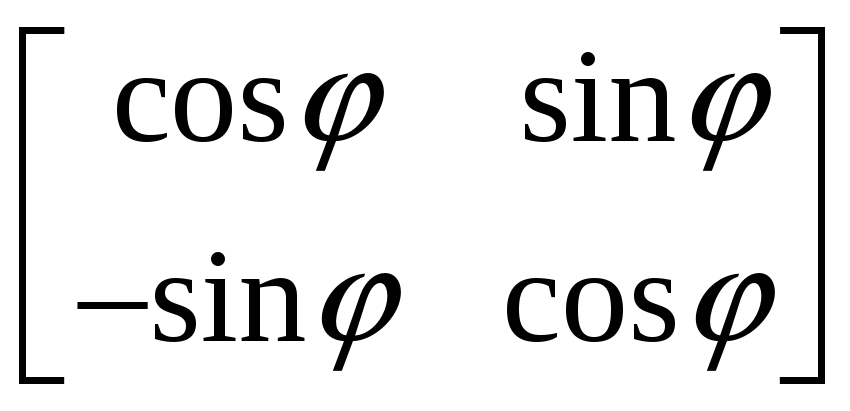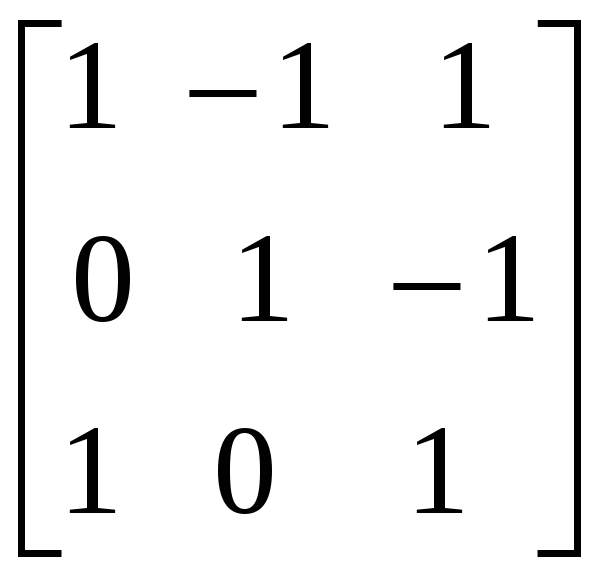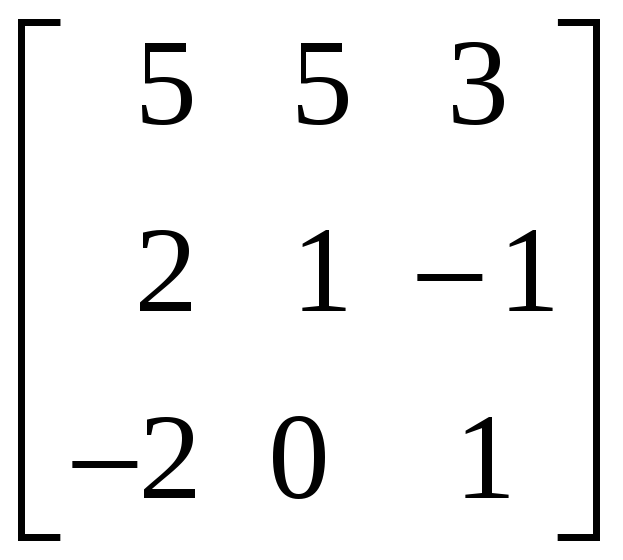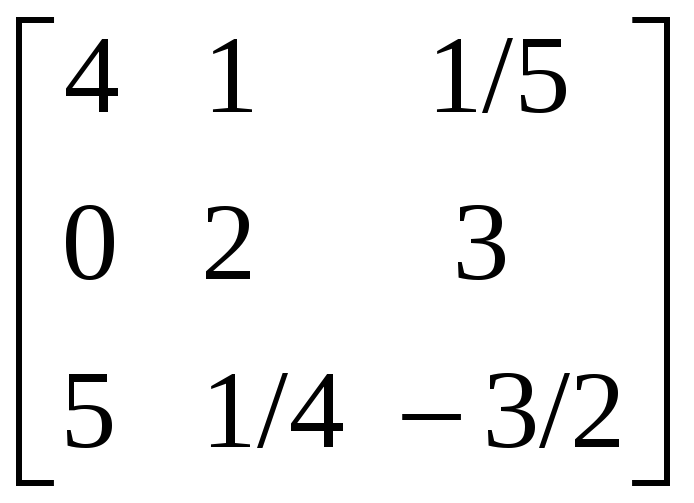2.3.2 Методом элементарных преобразований найти обратные матрицы для следующих матриц:

, , , , .

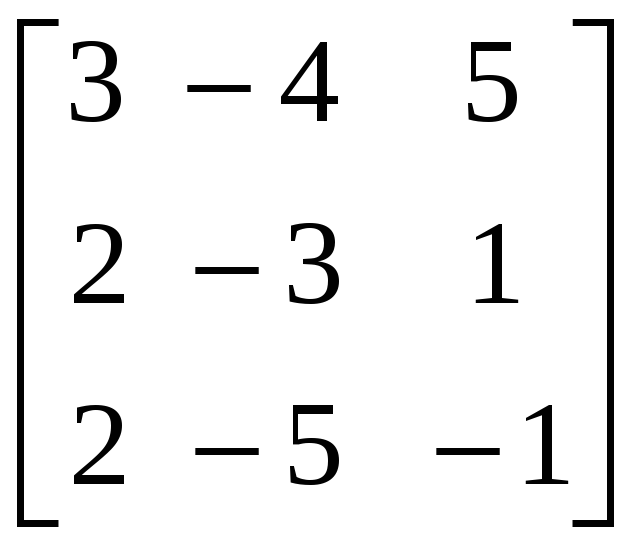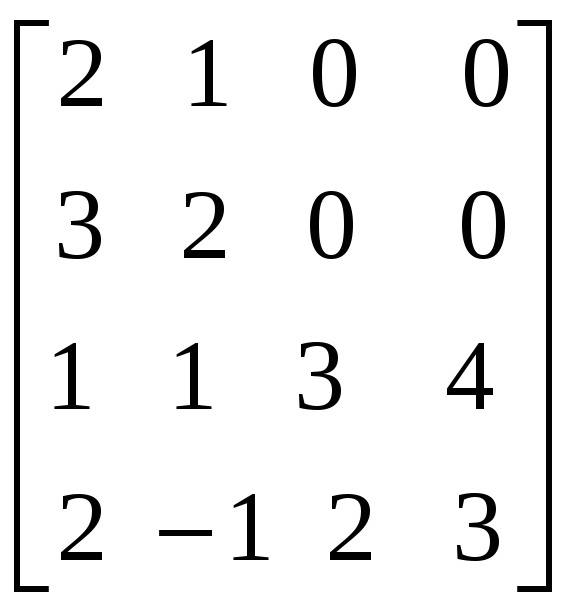2.3.3 Найти ранг матрицы методом окаймляющих миноров и указать какой-либо базисный минор:

, , , .

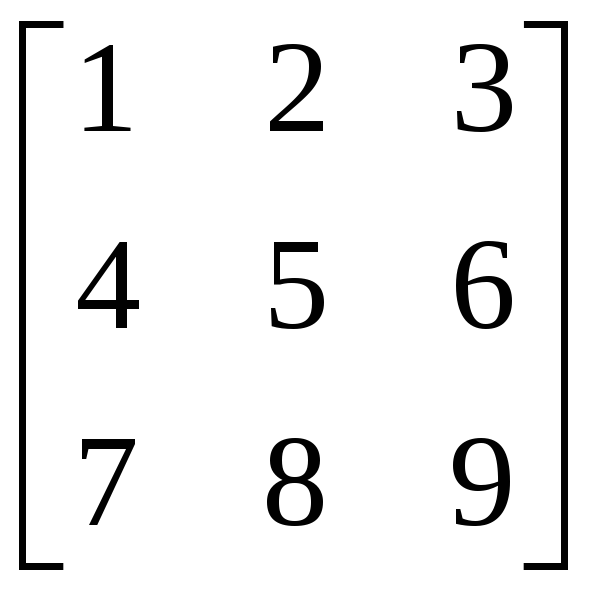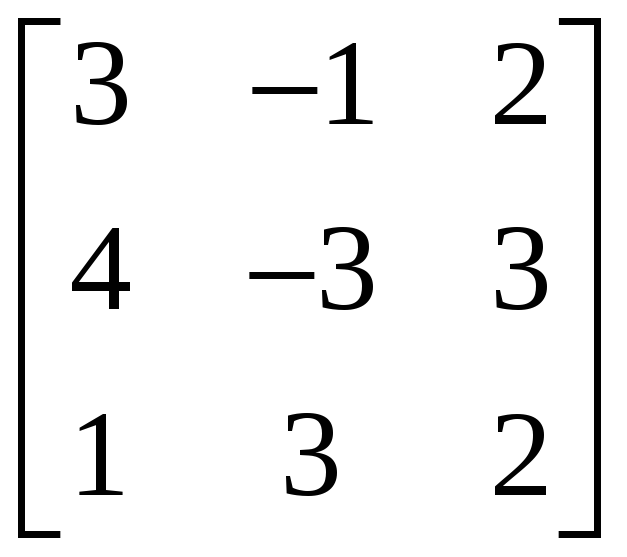2.3.4 Найти ранг матрицы методом элементарных преобразований:

, , .

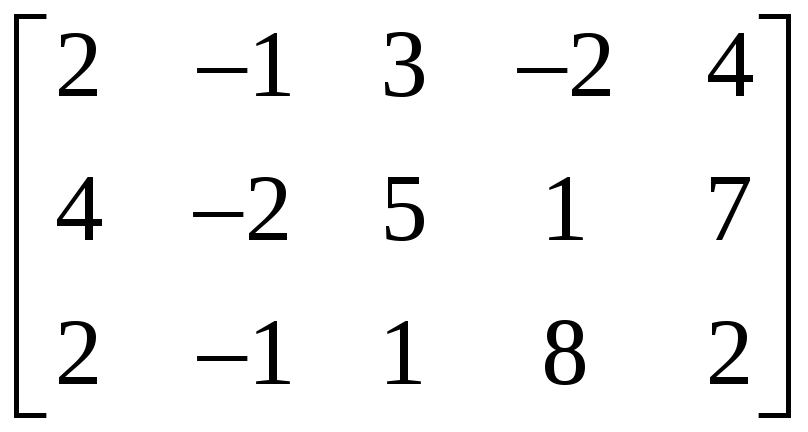2.4 Контрольные задания

Рекомендуемая литература [1, гл. 5, § 3, § 5], [2, гл. 1, § 1.9, § 1.13, § 1.16], [3, гл. 3 § 3.3, § 3.6].

2.4.1 Построить обратные матрицы для следующих матриц:

, , , .

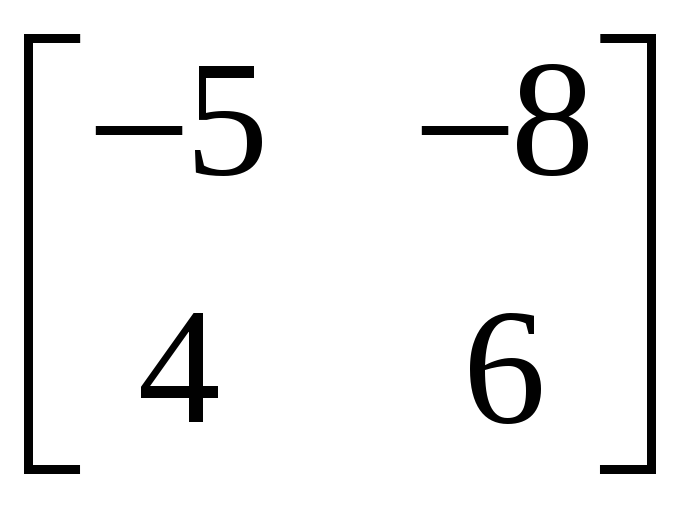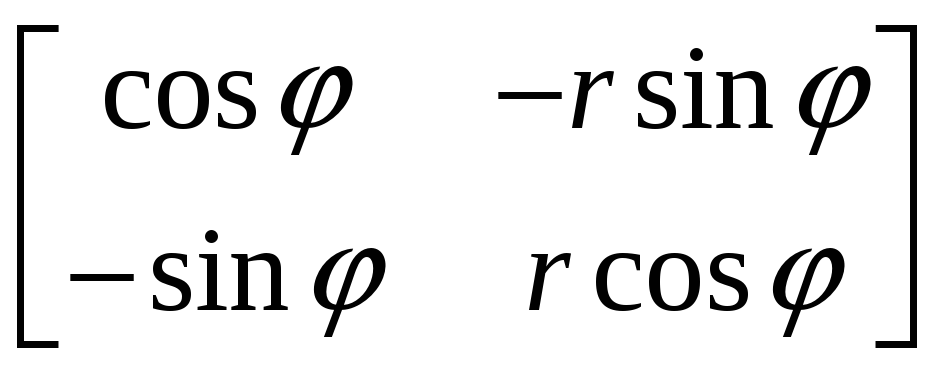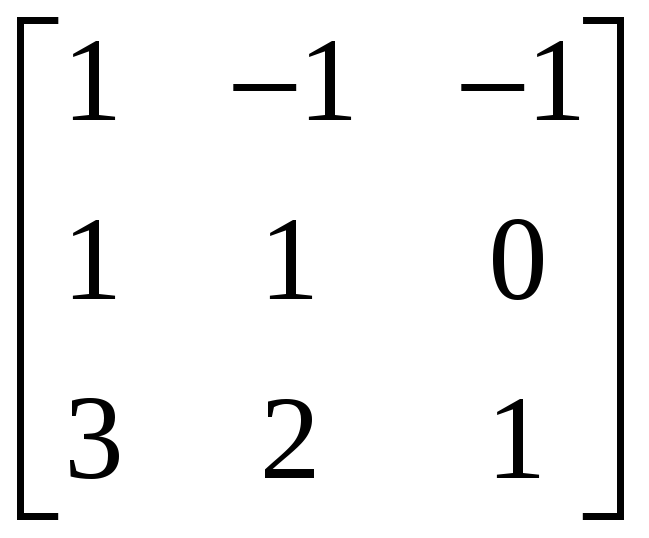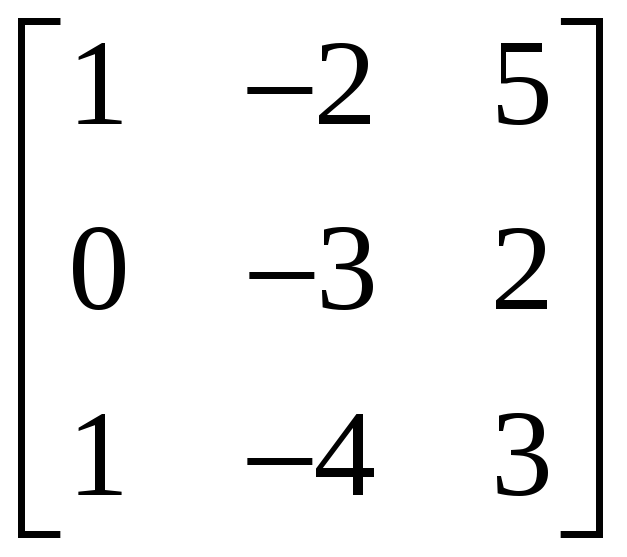2.4.2 Найти ранг матрицы и указать какой-либо базисный минор:

, , .

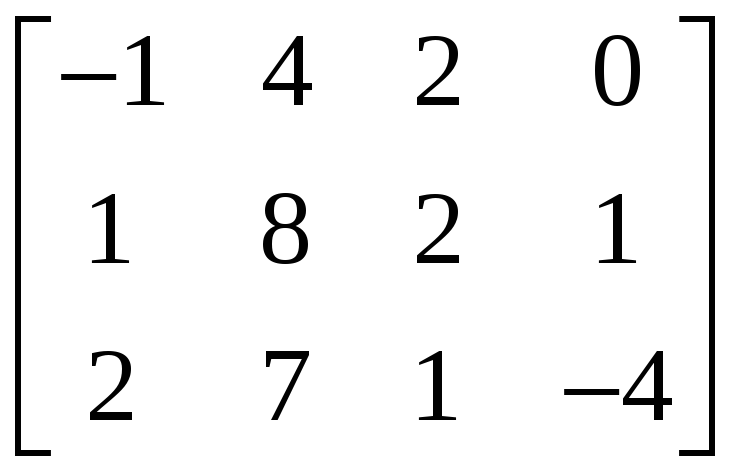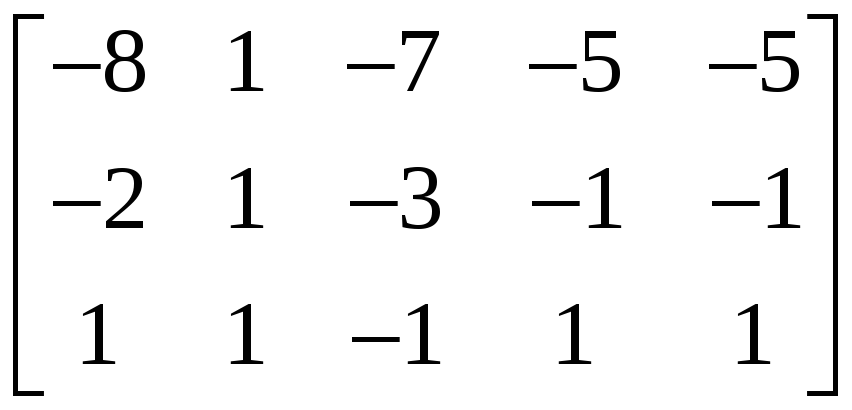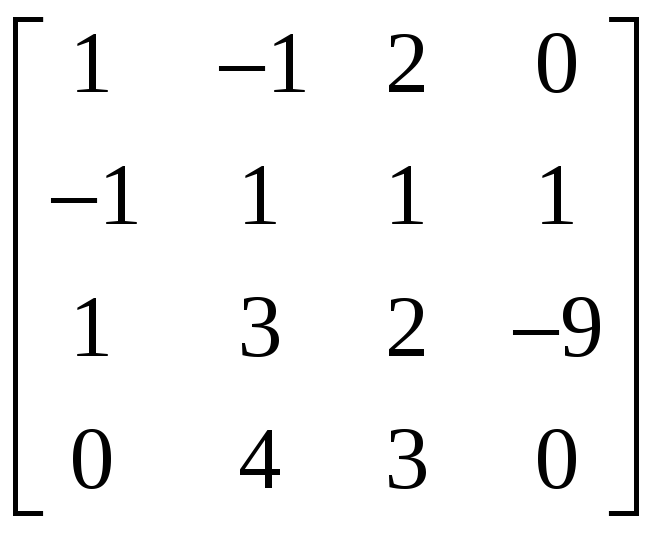3 Невырожденные системы линейных уравнений

Цель занятия: выработка навыков решения невырожденных систем линейных уравнений матричным методом и по формулам Крамера.

3.1 Матричный метод решения систем, формулы Крамера

3.1.1 Определение. Системой линейных алгебраических уравнений с неизвестными называется система вида

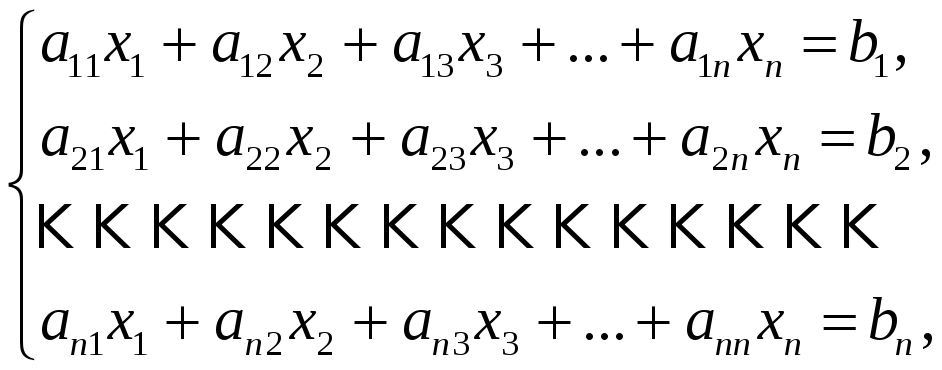(12)

где , – коэффициенты системы (12);

– неизвестные;

– свободные члены;

, .

Такую систему удобно записать в матричной форме

, (13)

где – матрица коэффициентов системы, называемая основной матрицей системы (12):

;

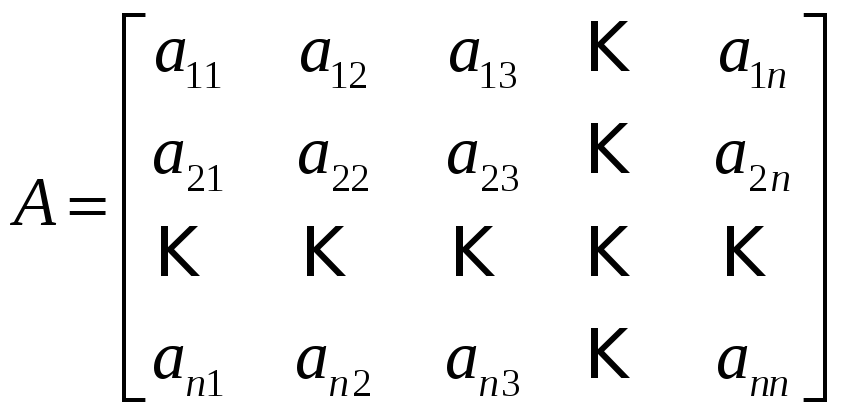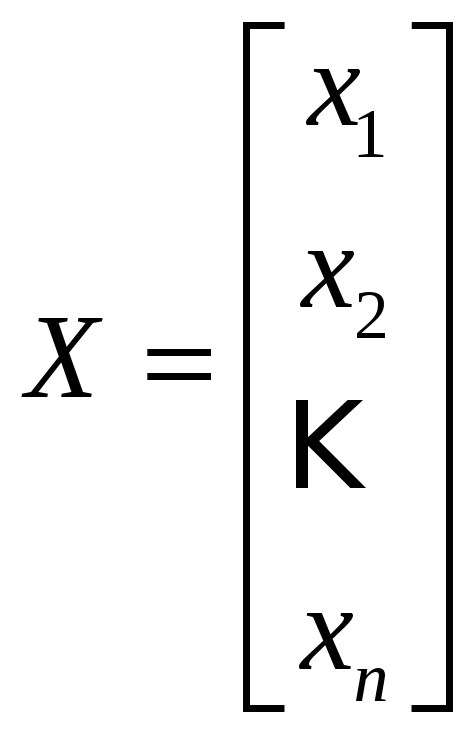– столбец неизвестных ,

– столбец свободных членов .

Если , то система (12) называется невырожденной.

Упорядоченный набор чисел называется решением системы (12), если каждое уравнение системы (12) обращается в верное числовое равенство после подстановки этих чисел вместо соответственно. Вектор с координатами называют вектор-решением системы (12).

Если система (12) невырождена, то матрица невырождена и имеет обратную матрицу . Тогда, умножая обе части матричного равенства (13) на слева, получаем

и, ввиду того, что , ,

. (14)

Выражение (14) даёт решение системы (12) в матричном виде. Метод нахождения решения системы (12) с использованием выражения (14) называется матричным.

При указанных условиях решение системы уравнений (12) единственно и может быть записано также с помощью формул Крамера:

, , …, , (15)

где – определитель, который получается из определителя путём замены -го столбца столбцом свободных членов:

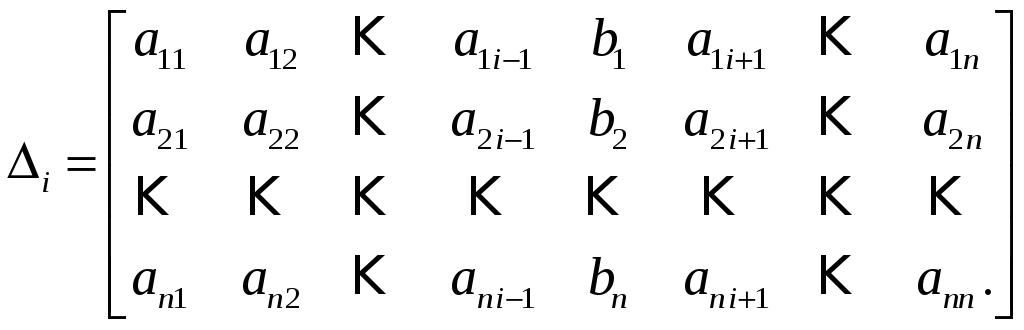(16)

3.1.2 Пример. Дана система уравнений

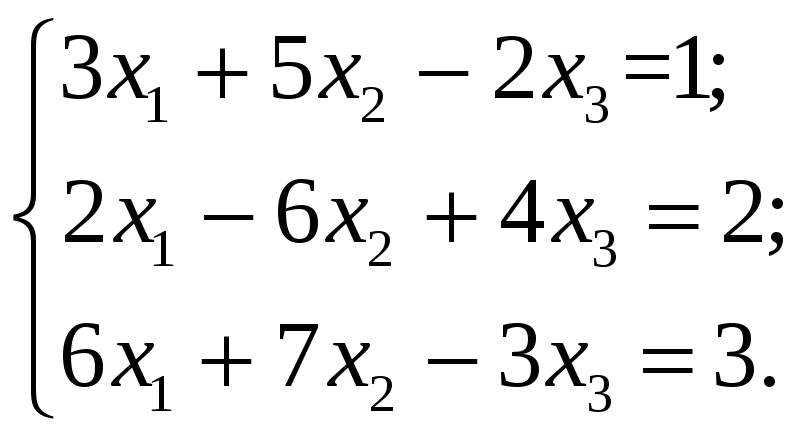
Решить её матричным способом и по формулам Крамера.

Решение.

1 Имеем:

, ,

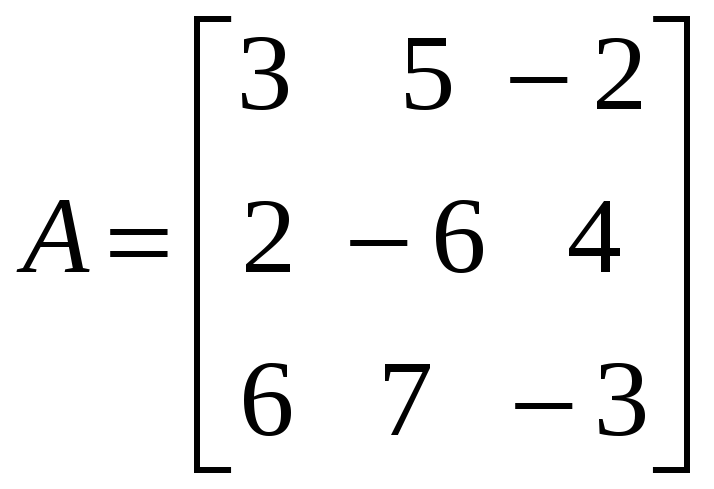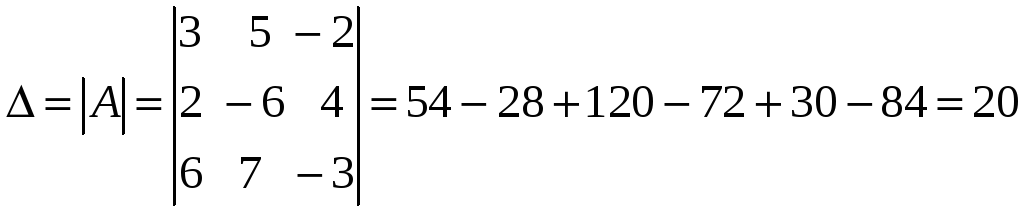т. е. матрица имеет обратную матрицу , которую мы построим согласно (10):

, , ,

, , ,

, , .

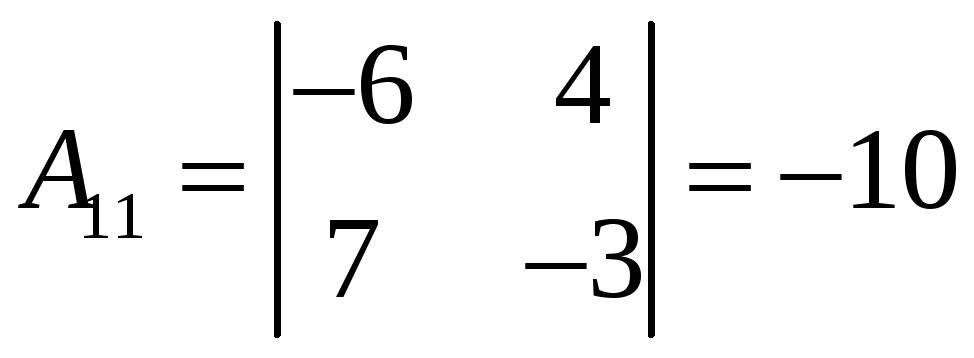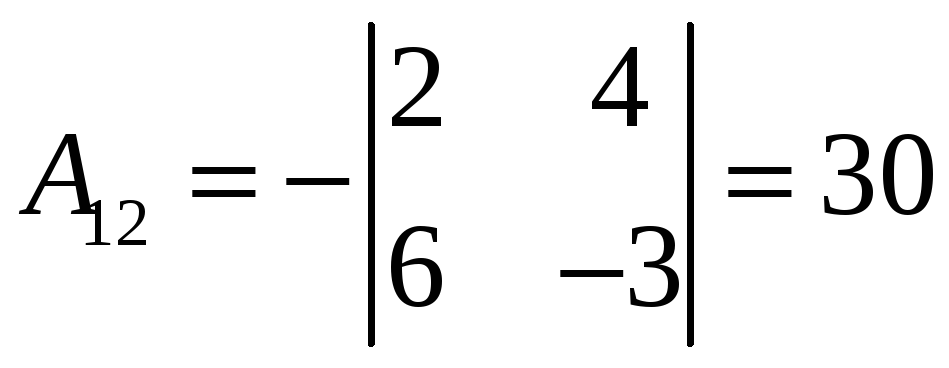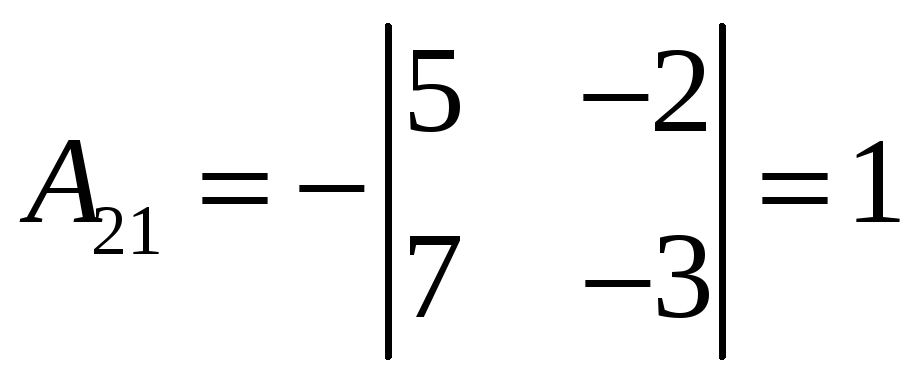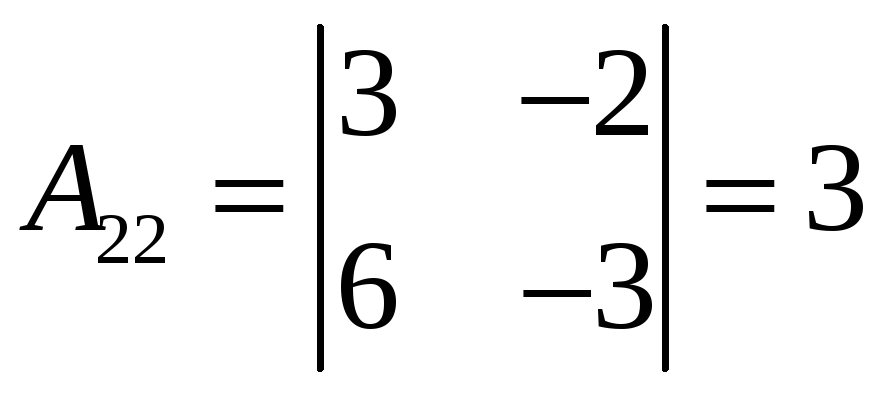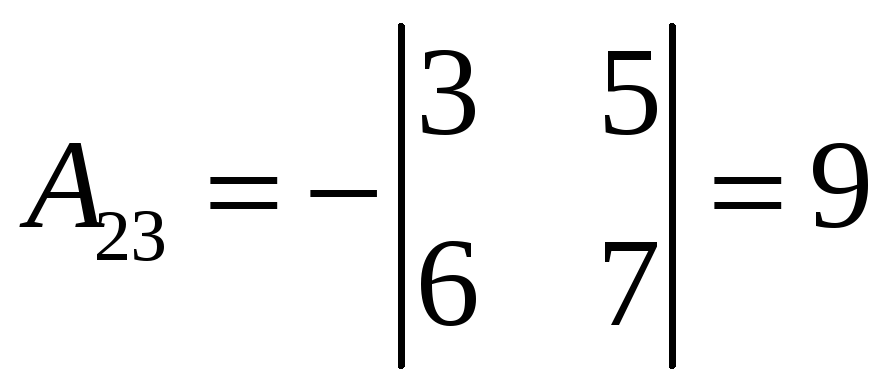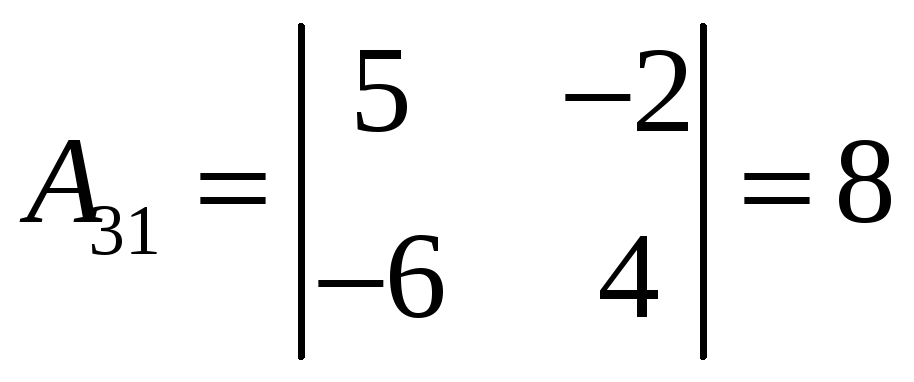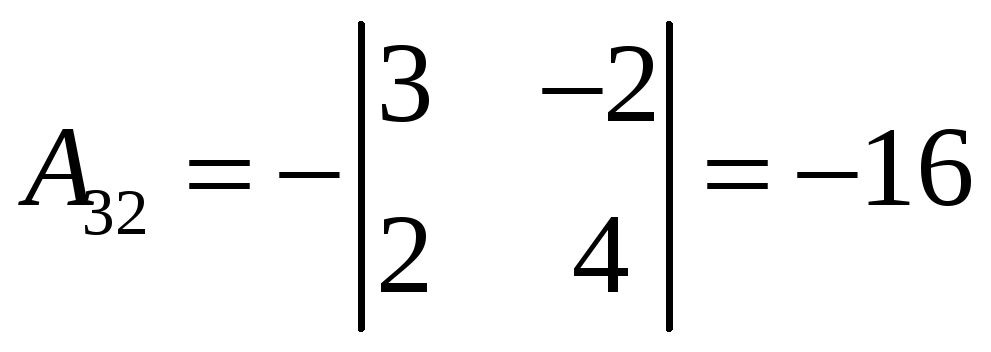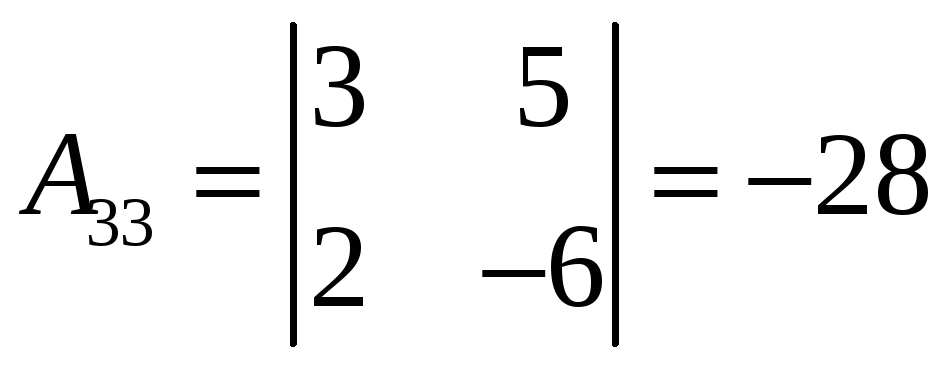Итак,

_.

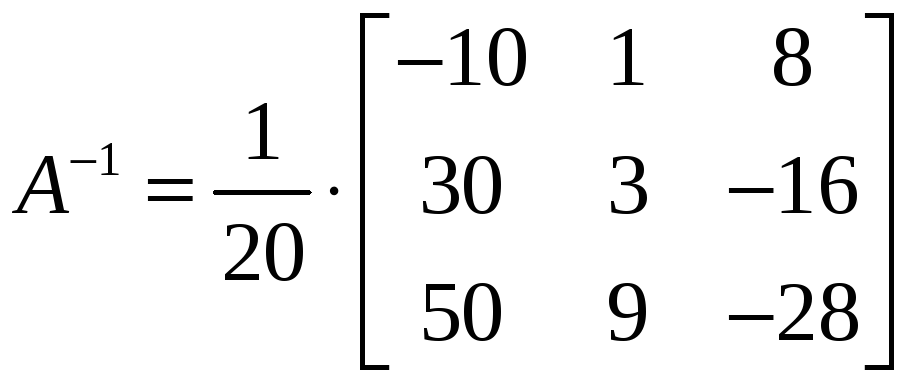По (14) получаем

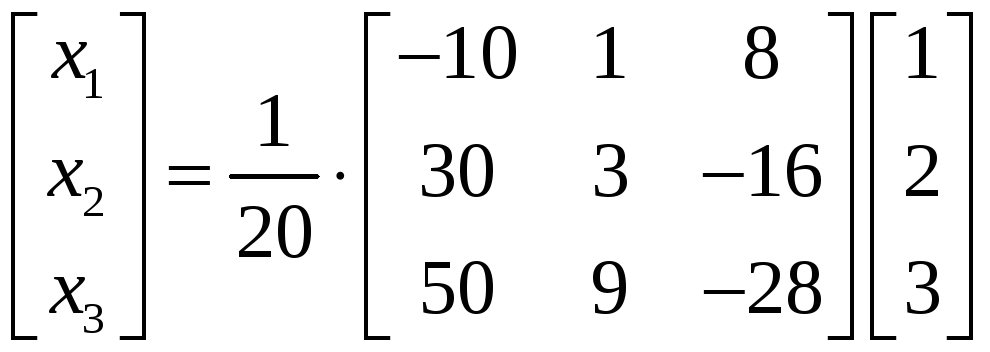, откуда

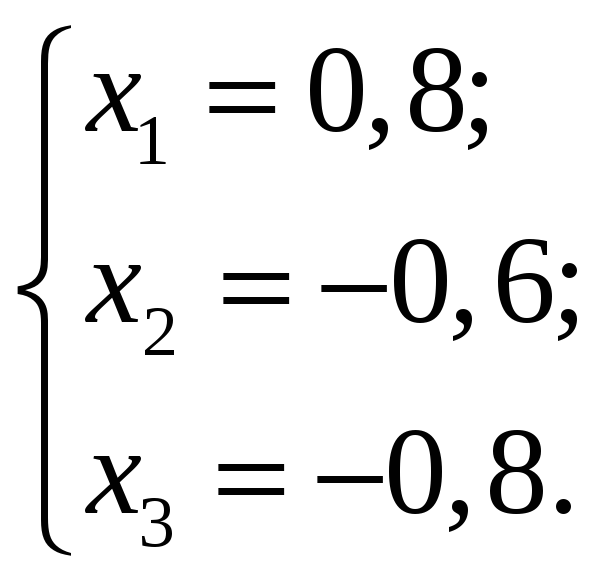
2 Вычислим: , , .

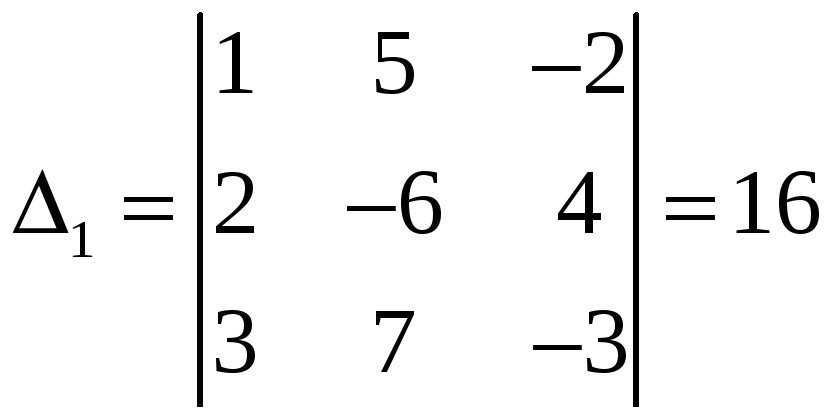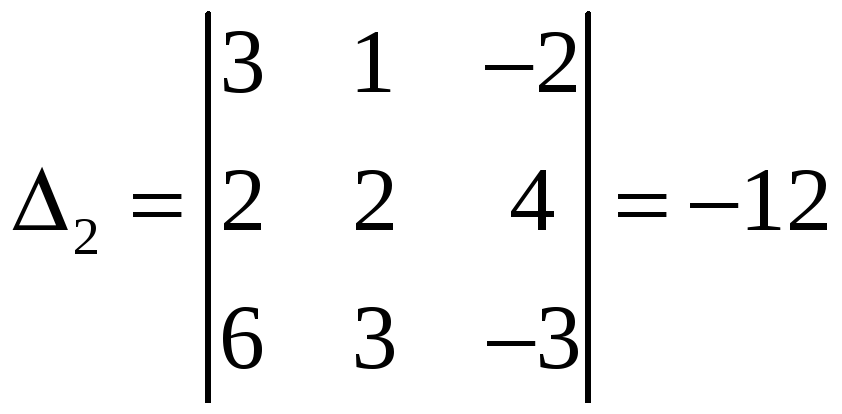По формулам Крамера имеем: , , .

3.2 Упражнения

3.2.1 Проверить, является ли система линейных уравнений невырожденной и решить её по формулам Крамера и матричным методом:

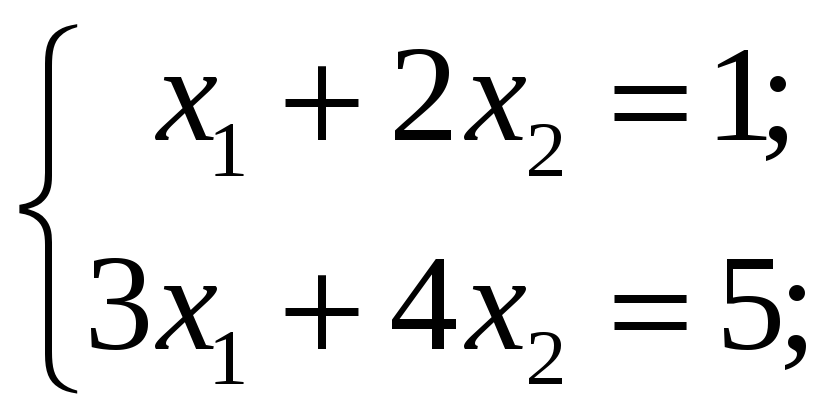
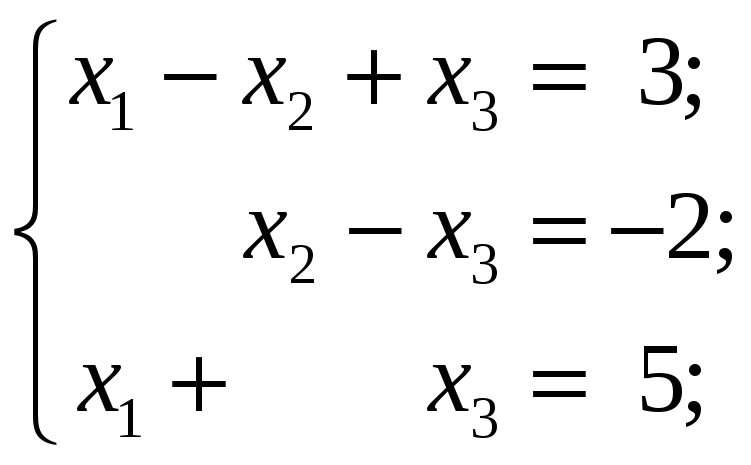
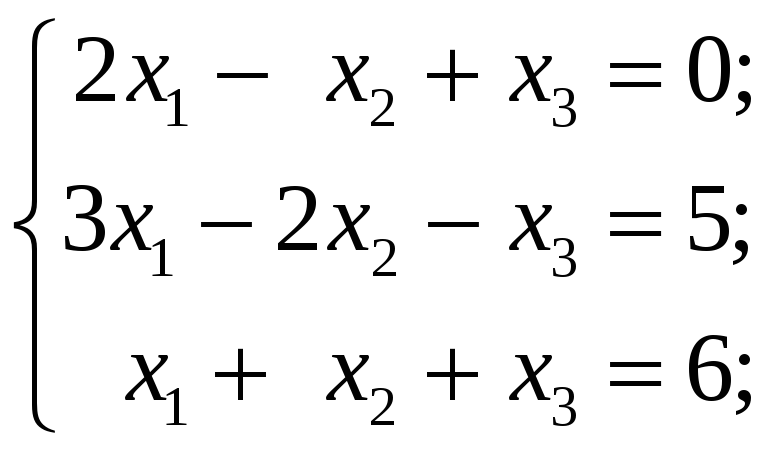
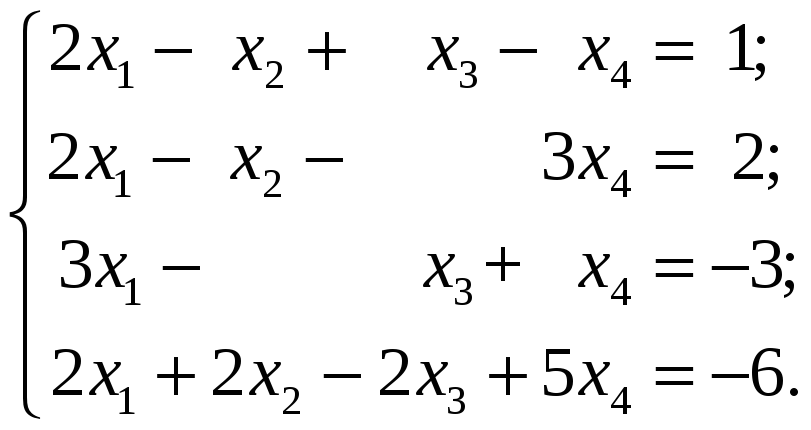
3.3 Контрольные задания

Рекомендуемая литература [1, гл. 5, § 2], [2, гл. 1, § 1.14], [3, гл. 3, § 3.4].

3.3.1 Решить следующие системы уравнений по формулам Крамера:

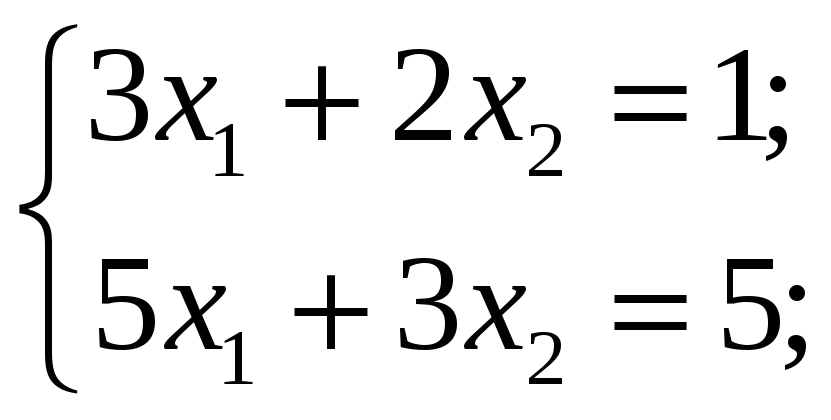
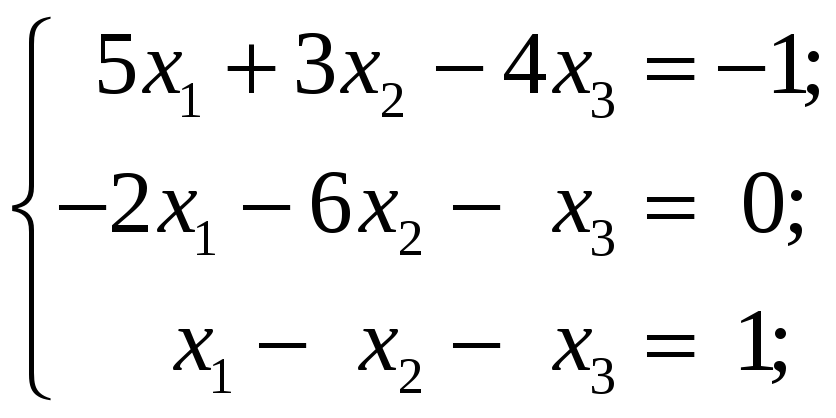
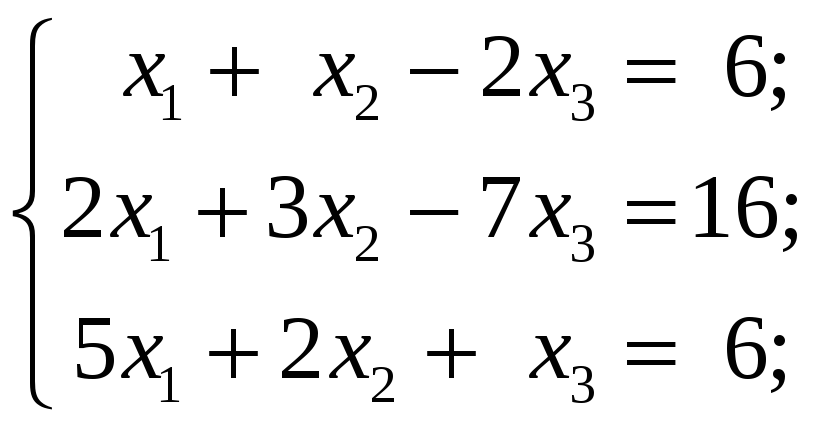
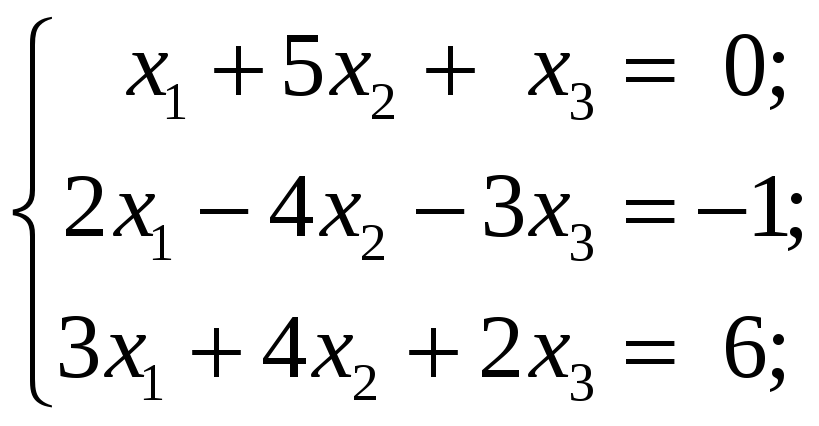
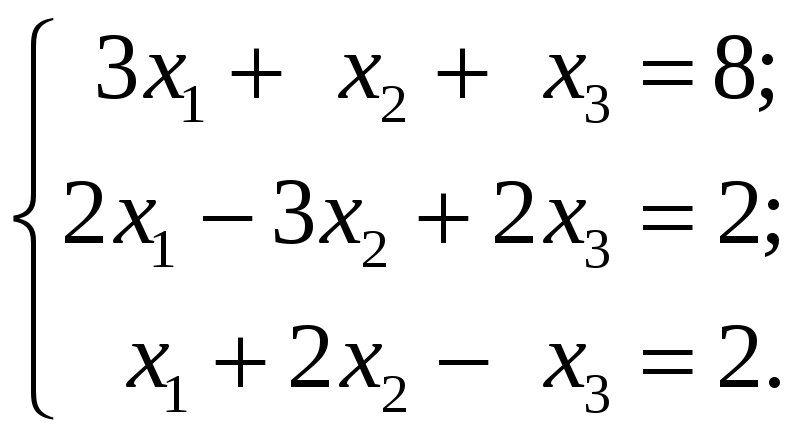
4 Решение произвольных систем

Цель занятия: выработка навыков исследования и решения систем линейных уравнений с неизвестными.

4.1 Основные понятия. Теорема Кронекера-Капелли

Рассмотрим систему линейных алгебраических уравнений с неизвестными:

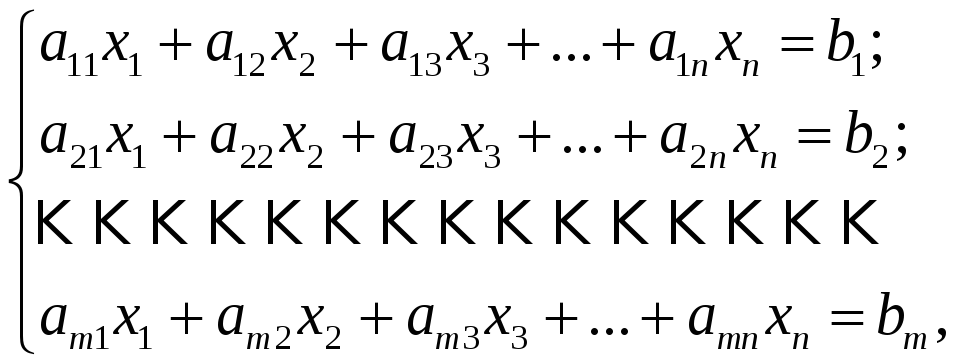(17)

где , – коэффициенты системы (17);

– неизвестные;

– свободные члены;

, .

Матрицы

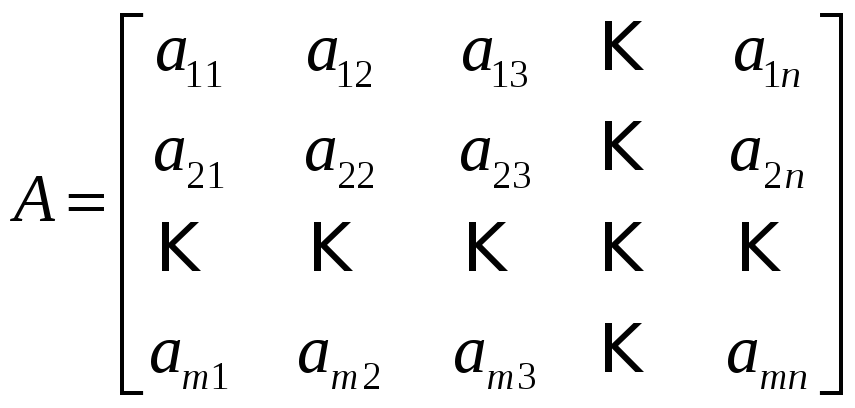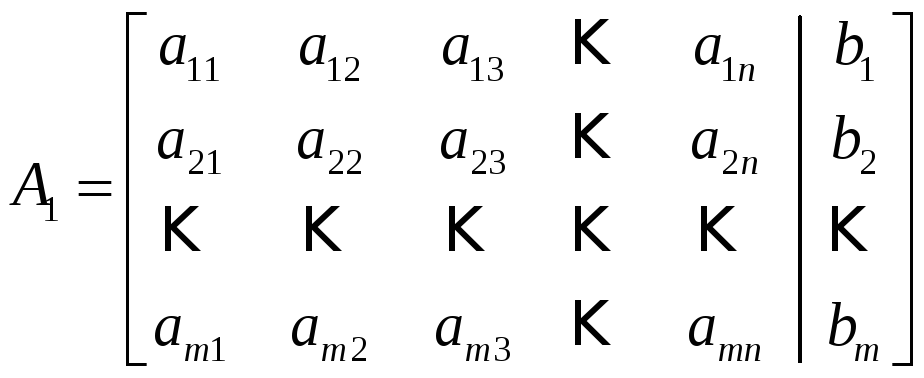, (18)

называются соответственно основной и расширенной матрицами системы (17). В матричном виде система (17) имеет вид (13).

Упорядоченный набор чисел называется решением системы (17), если каждое уравнение системы (17) обращается в верное числовое равенство после подстановки этих чисел вместо соответственно. Вектор с координатами называют вектор-решением системы (17).

Если система (17) имеет хотя бы одно решение, она называется совместной; система, не имеющая ни одного решения, называется несовместной. Система называется определённой, если она имеет единственное решение, и неопределённой, если она имеет более одного решения. Две системы уравнений называются эквивалентными или равносильными, если они имеют одно и то же множество решений.

4.1.1 Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений (17) была совместной, необходимо и достаточно, чтобы ранги основной и расширенной матриц системы (17) были равны.

4.1.2 Схема исследования и решения системы линейных уравнений.

4.1.2.1 Находим ранги и основной и расширенной матриц системы (18). Если , то система уравнений (17) несовместна и процесс заканчивается.

4.1.2.2 Пусть . Выделяем базисный минор матрицы . Те неизвестных системы, коэффициенты которых входят в базисный минор , называют базисными неизвестными, а остальные неизвестные системы уравнений называют свободными. Как правило, выбор базисного минора может быть осуществлён не единственным способом.

4.1.2.3 Заменяем систему (17) равносильной системой, состоящей из тех уравнений, которые содержат базисный минор. Свободные неизвестные переносим в правые части этих уравнений.

4.1.2.4 Решаем полученную систему уравнений, например по формулам Крамера, выражая базисных неизвестных через свободных неизвестных. Придавая свободным неизвестным произвольные значения, получаем бесконечное множество решений исходной системы уравнений. Например, в случае базисного минора, расположенного в первых () строках и столбцах матрицы , базисные неизвестные ,,…, однозначно выражаются для каждого фиксированного набора значений свободных переменных , , …, в виде выражений:

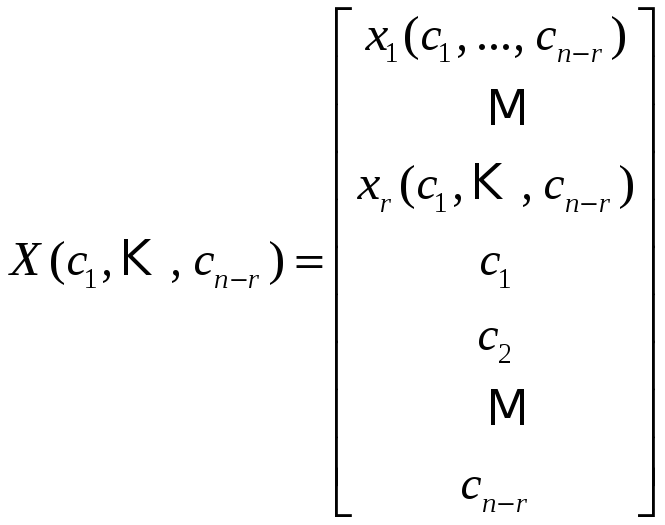. (19)

4.1.3 Определение. Общим решением системы (17) называется множество всех её решений, записанных в виде формулы (19), выражающей произвольное решение системы в виде функций от неизвестных. При этом каждое из решений указанного множества называется частным решением системы. Отметим, что если свободных неизвестных не будет (), то система уравнений имеет единственное решение.

4.1.4 Пример. Исследовать на совместность систему линейных уравнений

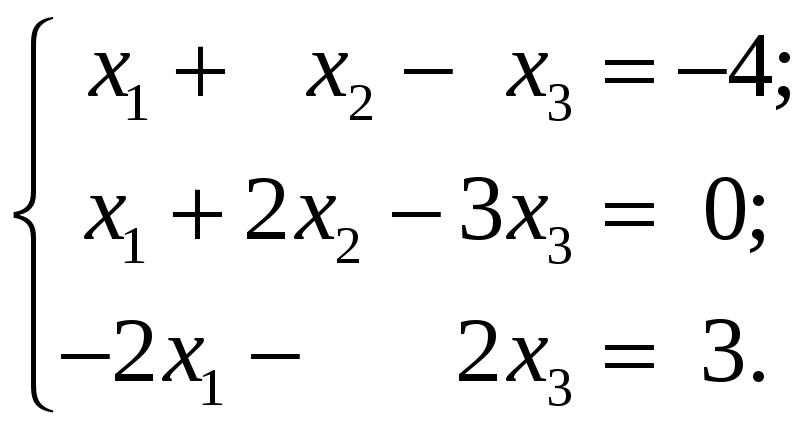
Решение.

Находим ранги матриц и с помощью элементарных преобразований строк:

.

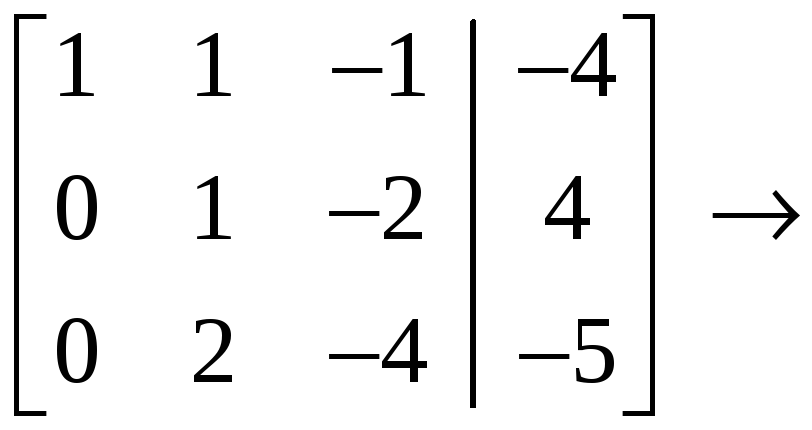
Отсюда следует, что , а значит система несовместна.

4.1.5 Пример. Исследовать на совместность систему линейных уравнений; если она совместна, то найти её общее и одно частное решение:

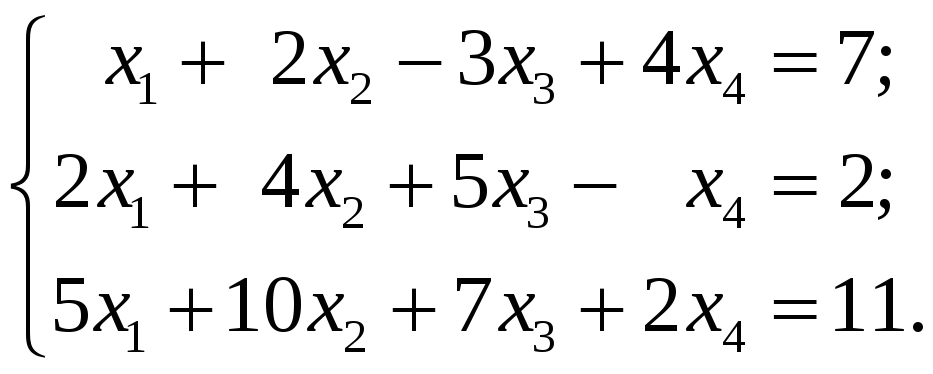(20)

Решение.

Анализ матриц и с помощью метода окаймляющих миноров показывает, что (значит система уравнений (20) совместна). Действительно, все миноры третьего порядка, окаймляющие ненулевой минор второго порядка 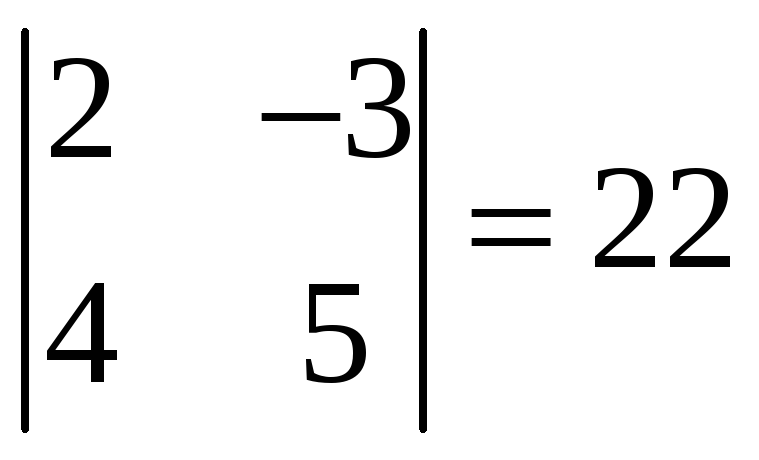, равны нулю:

, , .

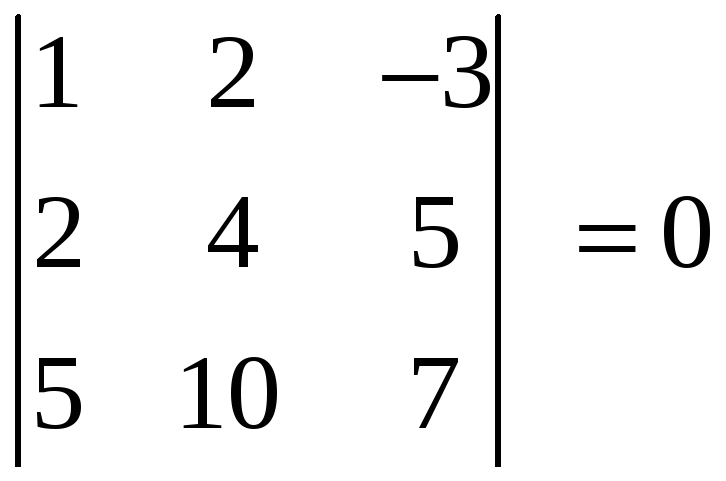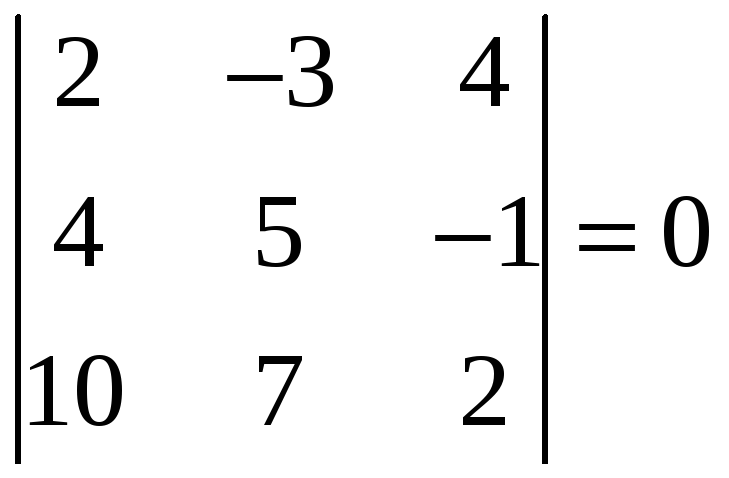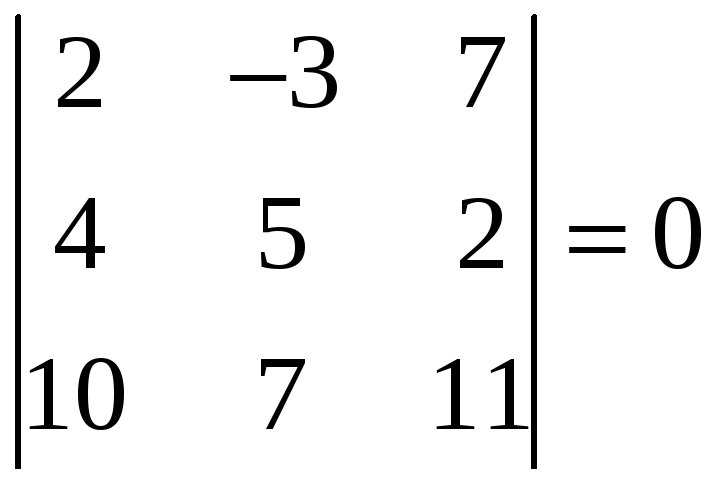Число базисных переменных равно , число свободных переменных . В качестве базисного минора возьмём рассмотренный 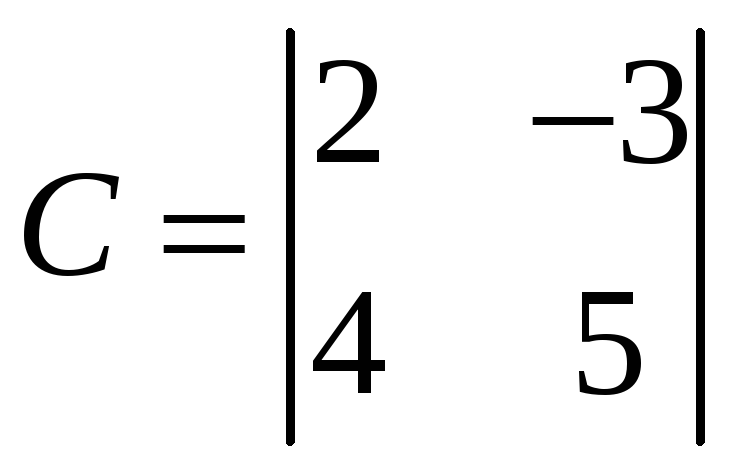. Тогда , – базисные неизвестные, и – свободные неизвестные. Записываем эквивалентную систему из двух уравнений:

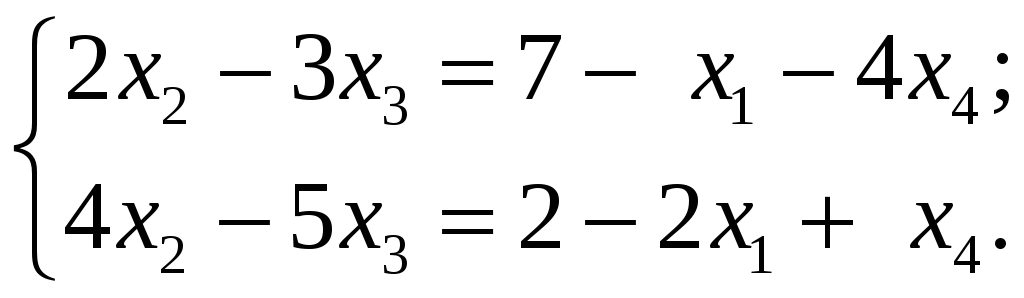
Находим решение данной системы по формулам Крамера:

, , .

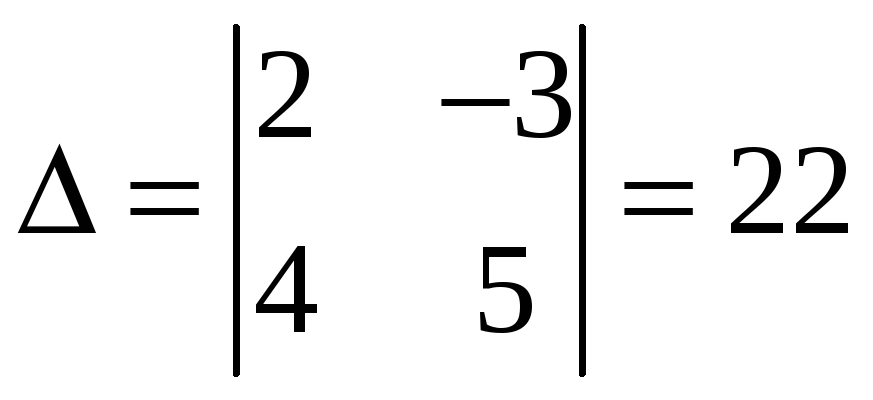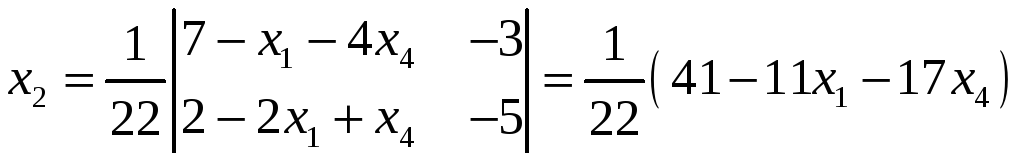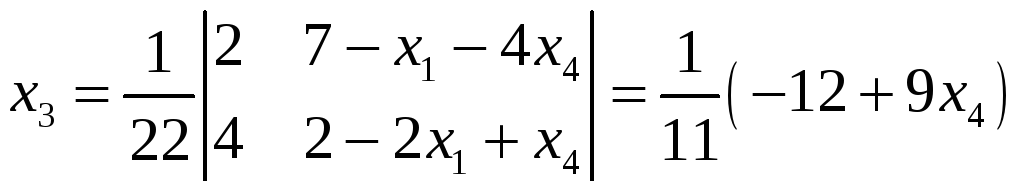Пусть , , где . Тогда общее и частное (при , ) решения исходной системы уравнений имеют вид:

, .
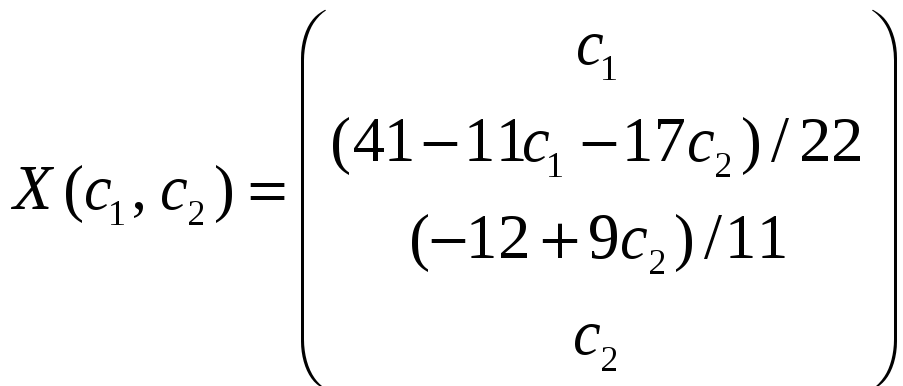
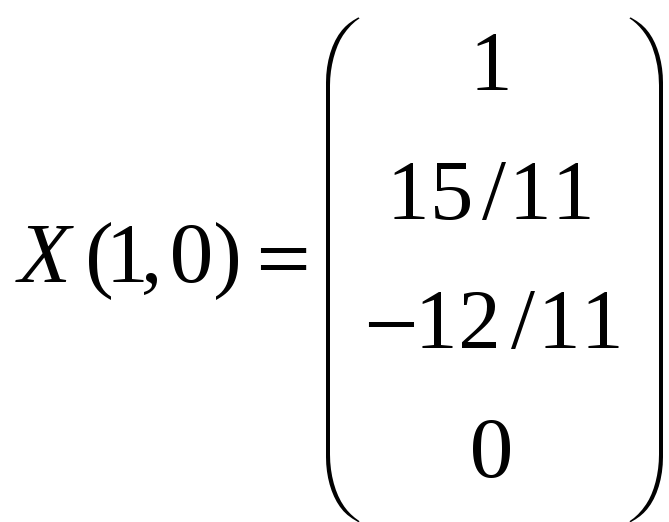