2.2 Ранг матрицы
В
матрице
размеров
выделим
произвольных строк и
произвольных столбцов:
,
.
2.2.1
Определение.
Минором
-го
порядка матрицы
называется определитель
-го
порядка, составленный из элементов
матрицы, расположенных на пересечении
выделенных
строк и
столбцов.
2.2.2
Определение.
Рангом матрицы
:
называется наибольший порядок отличных
от нуля миноров этой матрицы.
2.2.3
Определение.
Базисным минором матрицы
называется ненулевой минор порядка
,
где
– ранг матрицы
.
Рассмотрим два основных метода вычисления ранга матрицы.
Метод
окаймляющих миноров нахождения ранга
матрицы
состоит в следующем. Необходимо:
1)
найти какой-нибудь минор
первого порядка (т. е. элемент матрицы),
отличный от нуля. Если такого минора
нет, то
;
2)
вычислять миноры второго порядка,
содержащие
(окаймляющие
)
до тех пор, пока не найдётся минор
,
отличный от нуля. Если такого минора
нет, то
,
если есть, то
.
И т. д.
…
к)
вычислить (если они существует) миноры
-го
порядка, окаймляющие минор
.
Если таких миноров нет или они все равны
нулю, то
;
если есть хотя бы один такой минор
,
то
и процесс продолжается.
Метод элементарных преобразований основан на следующей теореме.
2.2.4 Теорема. Элементарные преобразования (см. п. 2.1.3) матрицы не меняют её ранга.
Используя
эти преобразования, матрицу
можно привести к так называемой
трапецевидной форме
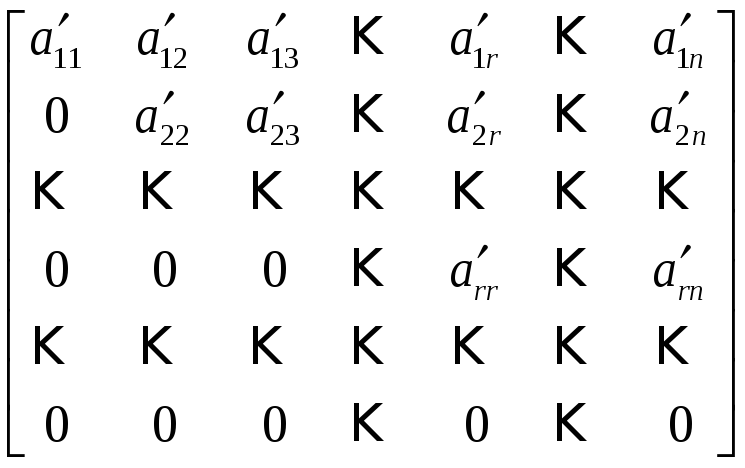, (11)
где
,
,
…,
отличны от нуля. В этом случае ранг
полученной матрицы равен
,
так как минор
=
,
а миноры более высоких порядков равны
нулю. Следовательно, ранг исходной
матрицы
также равен
.
2.2.5
Пример.
Найти ранг матрицы
методами окаймляющих миноров и
элементарных преобразований. Указать
какой-либо базисный минор.
Решение.
1
Так как у матрицы
есть ненулевые элементы, то
.
Найдём какой-либо ненулевой минор
второго порядка (если он существует).
Таким минором является, например,
.
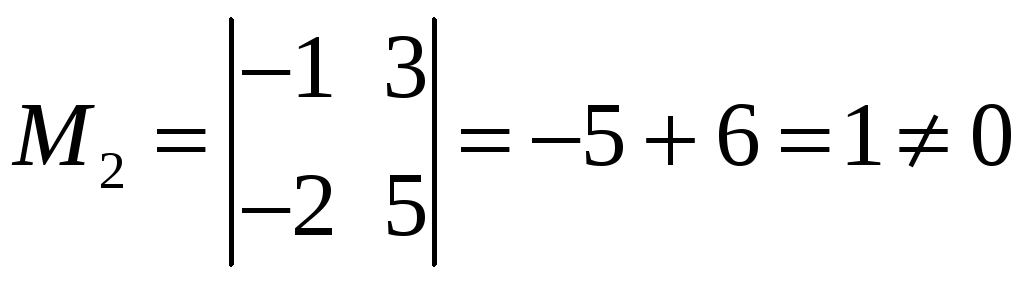Значит,
.
Вычислим окаймляющие его миноры третьего
порядка:
;
;
.
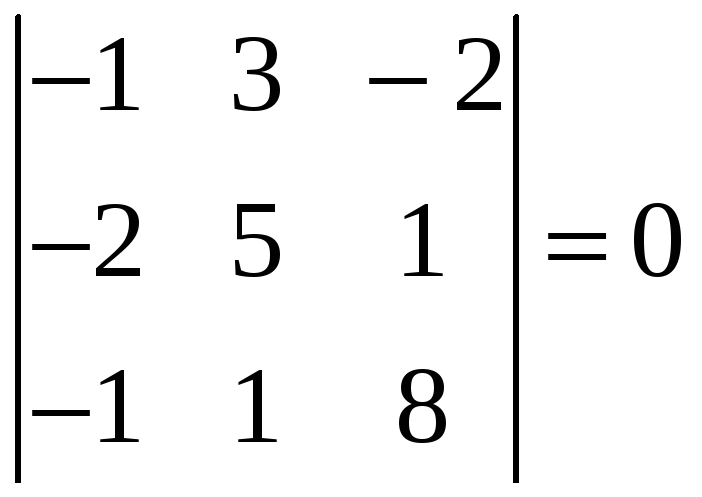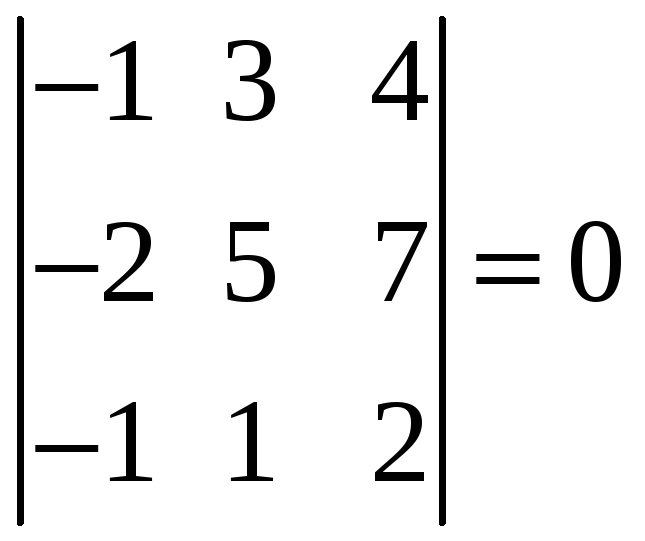Так
как не существует окаймляющих миноров
третьего порядка, отличных от нуля, то
.
Одним
из базисных миноров является указанный
ранее
.
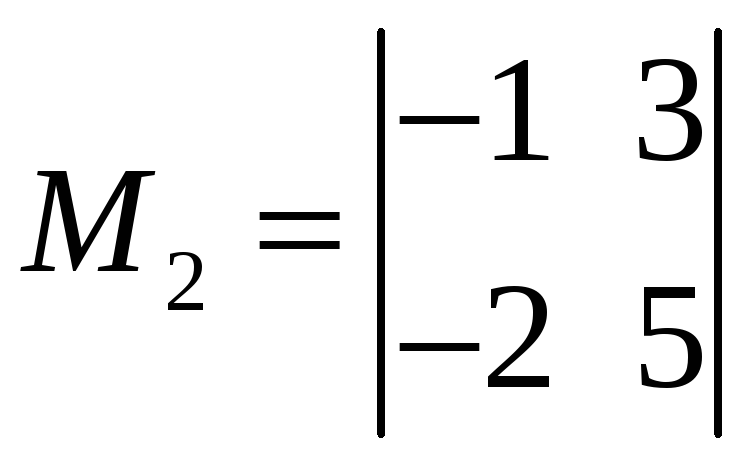2 Производя последовательно элементарные преобразования, будем иметь:
.
Здесь
вторая матрица получена из первой путём
поочерёдного умножения первой строки
на (
)
и (
)
и прибавления ко второй и третьей
строкам; третья матрица получена из
второй путём прибавления второй строки,
умноженной на (
),
к третьей. Ранг последней матрицы равен
двум, так как имеется отличный от нуля
минор второго порядка этой матрицы
,
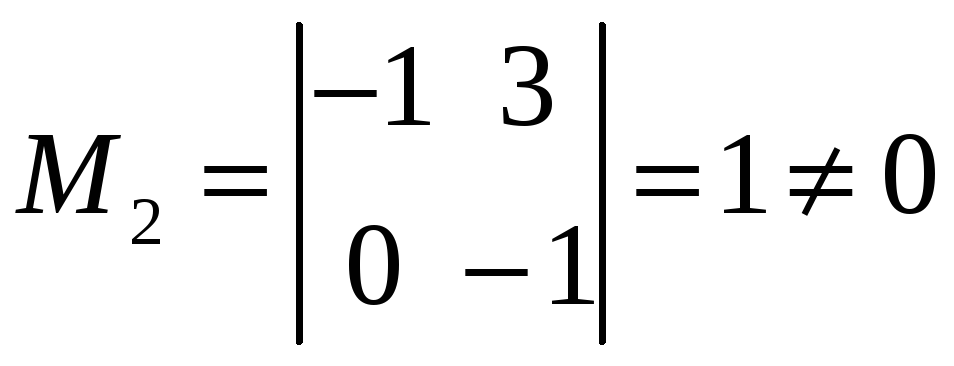а любой минор третьего порядка равен
нулю, поскольку содержит нулевую строку.
Следовательно
.
2.2.6
Пример.
Найти методом элементарных преобразований
ранг матрицы
.
Решение.
Производя последовательно элементарные преобразования, будем иметь:
.
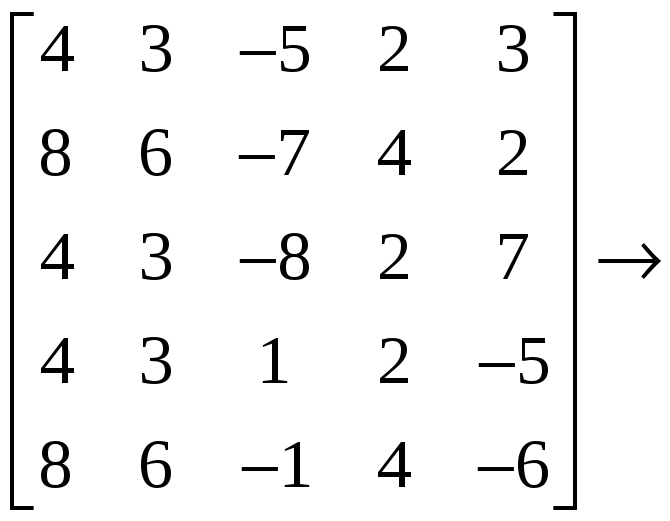
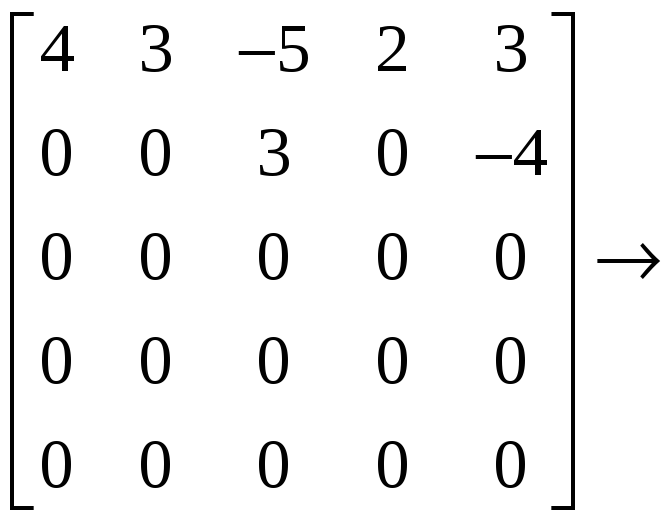
Получили
матрицу типа (11), у которой две ненулевые
строки. Из этого следует, что
.
Отметим также, что вывод
можно сделать, проанализировав уже
предпоследнюю (третью) матрицу.
Из неё видно, что отличны от нуля только
миноры первого и второго порядков,
например,
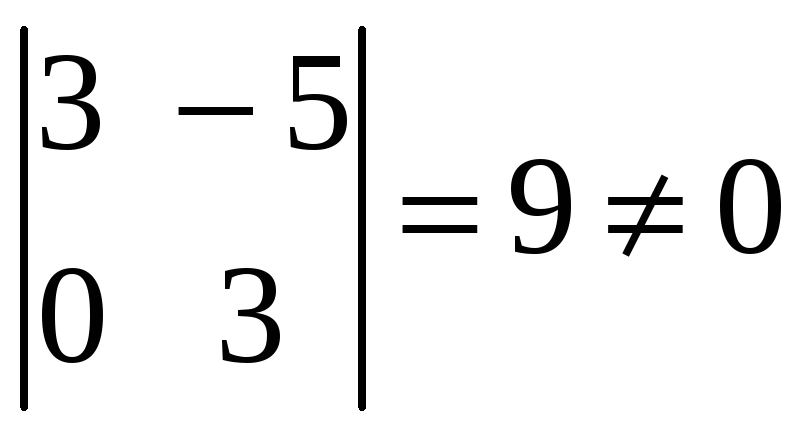(все миноры более высоких порядков равны
нулю).