Метод частичных областей. (процесс Трефтца)
Пусть имеется
область
,
которую можно представить в виде суммы
подобластей.
–
номер подобласти.
Обычно в каждой
из подобластей
и
постоянны. Пусть в каждой из подобластей
задача может быть легко решена (подобласти
простой формы).
Например, смотри рис.3.
Рис.3 Разбиение сложной области на простые.
Представления для полей в каждой из подобластей ищутся в виде:
,
(52)
где каждая пара
,
удовлетворяет уравнению Максвелла
поставленной задачи во всех внутренних
точках некоторой области
.
Поскольку представления
и
уже удовлетворяют уравнениям задачи,
остается лишь подчинить их краевым
условиям, что и делается путем
проецирования. Такой процесс называют
методом Трефтца. Выражения ( 52 ) – базис
Трефтца.
Пусть имеются такие границы
и
(
и
),
на которых требуется удовлетворить условиям непрерывности касательных электрических и соответственно магнитных компонент решения:
на
на
(
и
могут совпадать).
Тогда используя проекционные аналоги этих краевых условий
,
где фигурируют
полные (часто ортонормированные) системы
и
,
составленные из двумерных векторных
функций, заданных на соответствующих
границах. Метод частичных областей
(МЧО) приводит к проекционной модели
электродинамического объекта в виде
системы алгебраических уравнений
относительно коэффициентов
из
(52). Подчеркнем, что система функций
не
должна обладать полнотой в
или какой либо частичной области
,
однако существенна полнота на «границе
сшивания»
и
.
Если бы задача
решалась методом Бубнова – Галеркина
проекционная форма записывалась бы
для объема. Базисы
,
должны
содержать наборы гармоник по всем трем
направлениям (x,y,z).
При той же степени аппроксимации поля
количество базисных функций в процессе
Бубнова – Галеркина окажется значительно
больше.
Интегральные уравнения электродинамики.
Собственные волны волновода.
Так как собственные волны могут быть двух направлений,
+ направление + z (i – номер(тип) волны).
- направление – z
При этом
если
, если
;
здесь
– критическая частота для волны типа
;
потери в стенках отсутствуют.
Поперечные компоненты
,
где
– волновые сопротивления:
,
.
При
они
положительны
,
если же
,
то
,
.
Функции
и
образуют полные ортогональные системы
функций двумерного оператора Лапласа.
Ортонормировка этих функций
;
.
Вывод интегральных уравнений
Выше было показано, что располагая базисами Трефтца, уже не думают об удовлетворении уравнения во внутренних точках рассматриваемых областей. Все операции проводятся на их границах. Поэтому часто задачи электродинамики формулируют в такой форме, в которой фигурирует только эта граница.
Для простоты рассмотрим задачу дифракции электромагнитной волны для волновода с диафрагмой (Рис. 4).
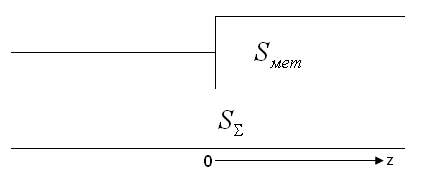
Рис.4. Диафрагма на стыке двух различных волноводов.
Пусть некоторая
волна первого
,
из первого волновода падает слева на
стык со вторым (z=0). Построим представление
поля в обеих полубесконечных подобластях:
(+ движение влево, – движение вправо).
, для
, для
Здесь использованы следующие обозначения:
и
–
комплексные амплитуды векторов поля
(точки сняты для простоты).
Электромагнитное поле в плоскости диафрагмы должно удовлетворять следующим граничным условиям
на
( 53 )
на
на
( 54 )
Первое из них ( 53 ) возьмем в проекционной форме:
( 55 )
Отсюда подставляя
и
получим
,
.
Подставляя в (55), получим
.
Пользуясь условием ортонормировки, найдем связь между коэффициентами
и
Найдем теперь
коэффициенты
.
Для этого обозначим тангенциальную
составляющую электромагнитного поля
в плоскости z=0
Введем обозначение
.
Для этого представим
ее в базисе
умножим скалярно
на
,
в результате получим
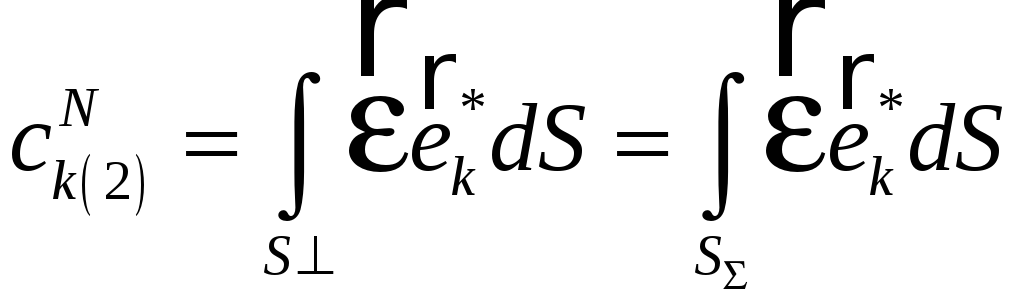
Теперь наложим граничные условия ( 54 ).
Для этого приравняем
выражения
и
.
При этом, входящие в них коэффициенты
и
,
мы уже нашли. В результате имеем
на
Упростим, для этого
умножим векторно на
и учтем
,
в результате получим:
Это интегральное
уравнение относительно неизвестной
функции
на отверстии
в плоскости диафрагмы.
Перепишем его в форме.
где
и
координаты в плоскости
,
причем
меняются в процессе интегрирования.
Ядро интегрального уравнения
равно
.
Оно имеет размерность проводимости, и такое интегральное уравнение называется админтансным.
Если изменить порядок наложения граничных условий ( 53 ) и ( 54 ) так, что сначала использовать ( 54 ) в проекционной форме, а затем наложить граничное условие ( 53 ), то получится интегральное уравнение относительно плотности тока на диафрагме
.
В этом случае интегральное уравнение будет иметь вид:
,
где
.
Ядро
– имеет размерность сопротивления, и
это уравнение называется импедансным.
Как адмитансное, так и импедансное интегральные уравнения могут быть решены методом Бубнова-Галеркина.