Интегральное уравнение Фредгольма.

Таким образом, для неизвестного распределения электрического поля (тока) в плоскости диафрагмы получим интегральное уравнение следующего вида:

.

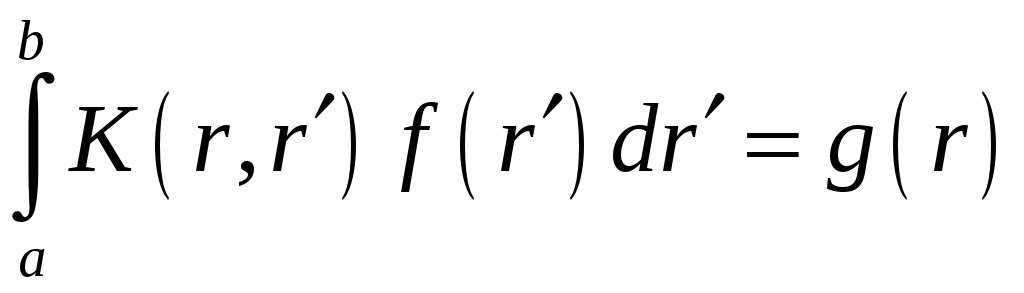Это интегральное уравнение Фредгольма 1-го рода.

Уравнение Фредгольма 2-го рода имеет вид

.

Переменные и меняются в одном и том же промежутке . Член - называется ядром интегрального уравнения. Он должен удовлетворять неравенству

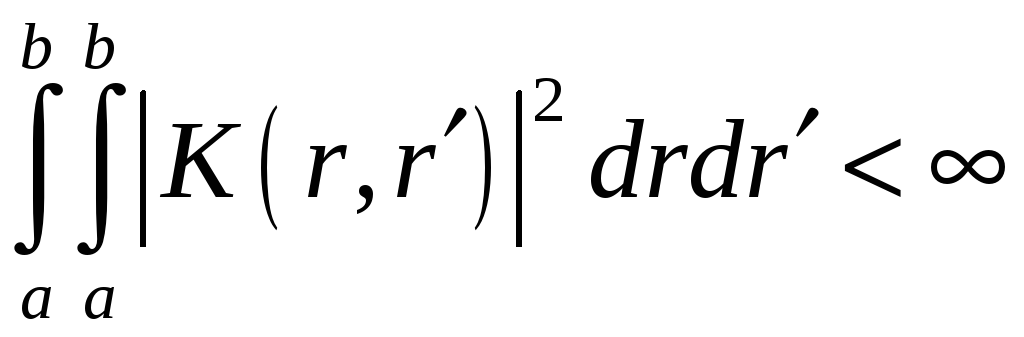
Ядро удовлетворяющее этому неравенству называется Фредгольмовым.

- свободный член уравнения Фредгольма должен удовлетворять неравенству

Выражение

определяет интегральный оператор, действующий в пространстве , он называется оператором Фредгольма. Этот оператор переводит любую функцию принадлежащую пространству в функцию того же пространства; он ограничен.

Решение интегрального уравнения

Как адмитансное, так и импедансное интегральное уравнение будем решать методом Бубнова-Галеркина . Запишем их в виде:

, где

, ,

, ,

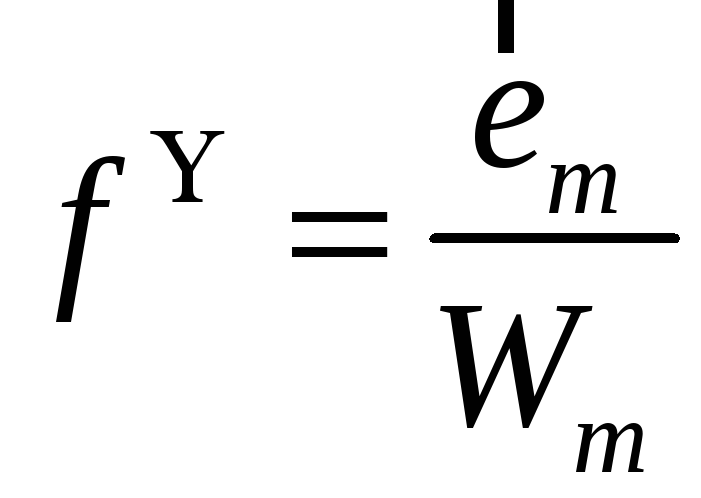а интегральные операторы имеют вид:

,

.

Выбрав какой-то базис на или, соответственно, на , запишем проекционное соотношение:

(56)

и представим решение в том же базисе:

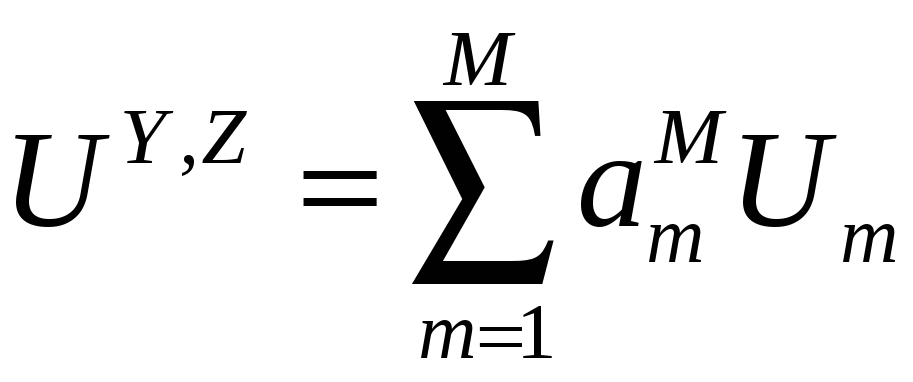(57)

Подстановка ( 57 ) в ( 56 ) приводит к системе линейных алгебраических уравнений.

,

где – вектор коэффициентов ( 57 ) ; матрица – имеет элементы

– сопряженная матрица,

так что

матрица , диагональная, причем

Вектор правой части имеет компоненты:

.

Решение интегрального уравнения для диафрагмы в плоском волноводе.

Геометрия рассматриваемой задачи изображена на рис.5. Волна распространяется вдоль оси Z.

Рис.5 Диафрагма в плоском волноводе.

Обозначим через (либо на, либо на металле )

.

Теперь необходимо выбрать систему функций . Из общих соображений, система функций по которой ведётся разложение, должна быть полной и ортогональной на отрезке . Кроме того, функции должны удовлетворять граничным условиям в точках 0 и c. таким условиям удовлетворяет, например, система

.

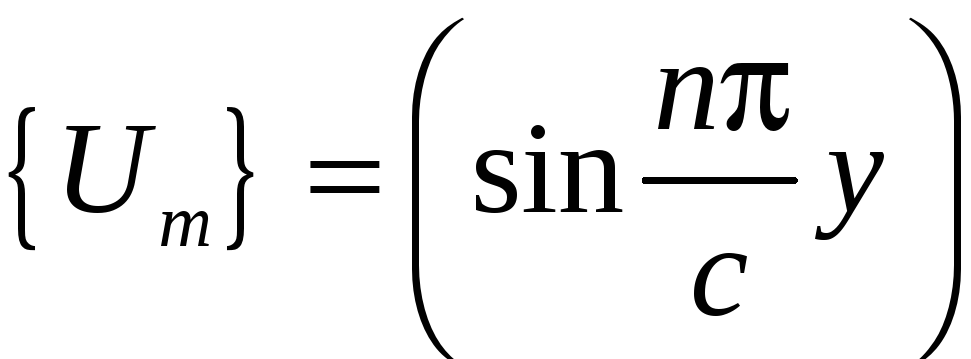Тогда наше интегральное уравнение перейдёт в систему линейных алгебраических уравнений (СЛАУ).

Каждый из матричных элементов представляется суммой где число мод в волноводе , то есть ядро выражено в виде ряда по модам волновода. Их в общем случае бесконечное число. Предположим, что при суммировании учитывается мод, то есть членов ряда.

Предположим, что при решении используется N базисных функций (N алгебраических уравнений системы) и Р членов в рядах ядра интегрального уравнения (Р число членов в рядах входящих в матричные элементы СЛАУ ).

Возникает естественный вопрос: зависит ли, и каким образом, приблизительное решение от выбора чисел N и Р. На примере различных задач для неоднородностей диафрагменного типа было показано, что решение для таких задач критично к выбору относительных значений N и Р. В частности, при решении матричного уравнения СЛАУ при фиксированных Р и переменных N, оказалось наилучшее приближение к точному решению достигается при некотором критическом значении , просто зависящем от выбранного значения Р и геометрии структуры.

Например, рассмотрим такую задачу: диафрагма перекрывает половину высоту волновода. Для этого случая известно точное решение задачи.

Нормированная входная проводимость связана с коэффициентом отражения продольной волны соотношением:

нормирована на проводимость подводящего волновода.

Точное значение шунтирующей проводимости для , полученное методом Винера-Хопфа, равно

;

.

Рис.6 Эквивалентная схема шунтирующей проводимости.

Рассмотрим зависимость при различных значениях .

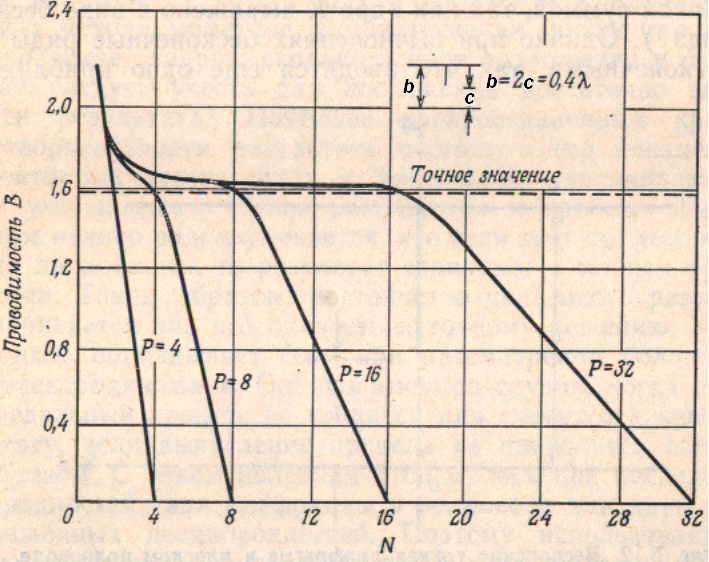
Рис.7 Зависимость шунтирующей проводимости при фиксированных значениях Р.

В частности из графика видно, что при некотором критическом значении , просто зависящем от , и .

Ясно видно, что численные результаты быстро ухудшаются, по мере того как N превышает критическое значение. В частности, при N=Р, полученное численным методом значение проводимости оказывается равным нулю, то есть действие неоднородностей как бы исчезает, то есть результат заведомо ошибочный.

Рис.8. Зависимость шунтирующей проводимости при фиксированных значениях N.

На этом рисунке представлены аналогичные зависимости, вычисленные при фиксированных значениях и меняющемся . Видно, что проводимости вначале меняется с ростом , а после превышения некоторого критического числа , определяемого формулой

достигает предельного постоянного уровня. Из графиков видно, что при приближение тем лучше, чем больше N.

Как показывают результаты расчетов, вычисленные значения проводимости быстрее всего сходится к точному значению, если

( 58 )

Принятие надлежащего значения обеспечивает улучшение скорости расчётов. Это явление получило название "относительная сходимость". Соотношение ( 58 ) носит название соотношение Митры.