Проблема устойчивости решения.

Очень важно исследование устойчивости системы. Решение плохо обусловленной системы (т.е. системы, детерминант матрицы которой близок к нулю), может быть не устойчивым.

В качестве примера рассмотрим сначала хорошо обусловленную систему

Она имеет единственное решение x=1, y=1.

Решение возмущённой системы: (значение одного из коэффициентов изменим на 1%)

имеет вид:

.

Т.о. изменение коэффициента на 1% приводит к изменению решения на 1%.

Теперь рассмотрим плохо обусловленную систему:

Она также имеет решение x=1, y=1.

А теперь возьмём три системы, полученные из исходной малым изменением коэффициентов:

;

;

;

Эти системы имеют решения:

, ;

, ;

, .

Мы видим, что при изменении коэффициентов на доли процента относительные изменения решений могут составлять сотни процентов.

Такое поведение решения плохо обусловленной системы уравнений следует всегда иметь в виду, так как при применении численных методов решения, через СЛАУ вероятность этого велика. Сильная зависимость решения задачи от некоторых параметров может объясняться не ошибками при формулировке задачи или составлении расчётной программы, а степенью обусловленности системы уравнений. Хотя при слабо обусловленных системах уравнений можно иногда получить верные решения, если проводить тщательный анализ возможных источников численных ошибок при вычислении коэффициентов. Обычно для исправления положения требуется изменить базисные функции.

Важной характеристикой метода расчёта, в котором решение сводится к СЛАУ, является устойчивость получаемой системы. Качественным критерием устойчивости системы

может служить число обусловленности cond(D), определяемое как произведение норм прямой и обратной матрицы.

Норма матрицы (кубическая) вычисляется

На рис.9 изображена зависимость числа обусловленности для задачи о дифракции волны на произвольной неоднородности от отношения P/N.

Рис.9. Зависимость числа обусловленности от отношения .

Если имеется узкий минимум на кривой, то это соответствует соотношению Митры.

Особенность на ребре.

В тех случаях, когда граничная поверхность имеет геометрически сингулярные точки, то есть точки, в которых функции, определяющие поле, определенны неоднозначно и не дифференцируемы, можно получить математически вполне корректных решений уравнений Максвелла, однако лишь одно из них будет правильно отражать структуру поля. Такими точками, в частности, являются, например, рёбра на граничных поверхностях волноводов, диафрагмы и т.д.

Для обеспечения единственности решения необходимо ввести дополнительное физическое ограничение, которое носит название "условие на ребре" (условие Мейкснера) (Мейкснер – 1954г; Гринберг – 1938г). Оно заключается в требовании конечности энергии электромагнитного поля, запасенной в произвольном конечном объеме в окрестности ребра, т.е. условием

,

при стремлении к нулю объема V в окрестности ребра.

Рассмотрим для простоты такую задачу (рис.10).

Рис.10. Произвольное двугранное ребро в волноводе.

Пусть . При переходе на ребро функция F должна оставаться конечной, а производные от неё должны обращаться в бесконечность. Введём цилиндрическую систему координат .

Где

Тогда уравнение Гельмгольца

с помощью подстановки

уравнение Гельмгольца преобразуется к виду:

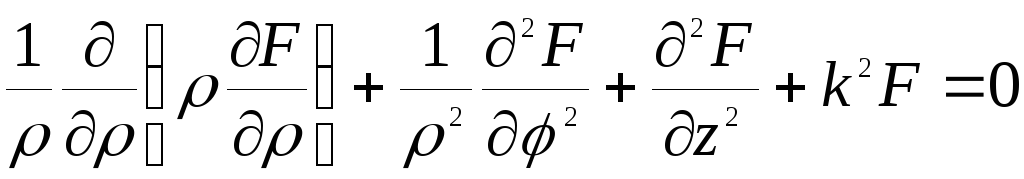
Выберем

.

При такой подстановке уравнение примет вид:

Для определения при получим уравнение

.

Его решение имеет вид:

Это соотношение пригодно для любого двухгранного угла. Потребовав обращение в нуль F на обеих гранях ребра (при и ), получим

.

Исключая постоянные А и В, найдём выражение для нахождения в виде

.

Рис.11. Бесконечно тонкий идеально проводящий гребень и идеально проводящий прямоугольный клин.

Удовлетворить этому равенству для идеально проводящего бесконечно тонкого гребня (; ) можно при . Аналогично для идеально проводящего прямоугольного клина при ; имеем 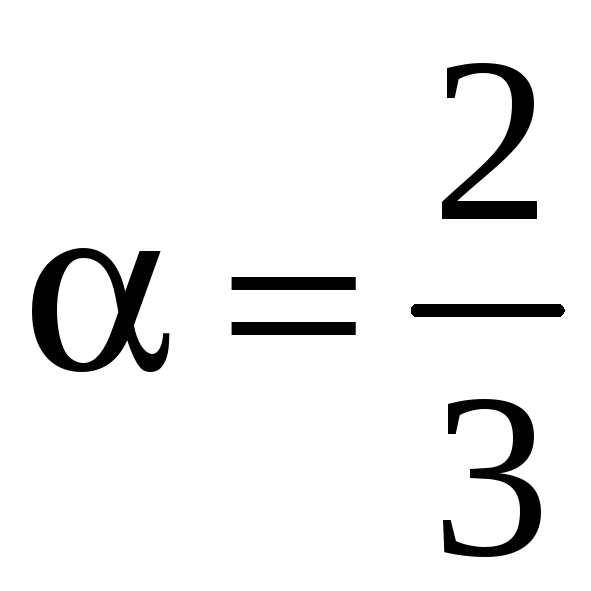. В результате для z – ых составляющих полей получим соответственно

и .

Так как и пропорциональны производным по поперечным координатам от и , то соответственно

и .