Дискретизационные методы Метод коллокации.

Рассмотрим некоторую задачу, сформулированную в виде:

Сохраним представление решения в виде:

.

Выделим в области существования решения систему точек, как это показано на рисунке 12:

r_i

V

Рис.12. Система точек в области существования рещения.

Сшивание в дискретных точках.

Если в качестве весовых функций в методе моментов выбрать дельта функции.

W_m=(-_m)

- текущая координата, а – координата точки, в которой необходимо удовлетворить граничным условиям.

Нижний индекс у функции …. показывает, что удовлетворяется условие в точке 1,2,… Использование -функций показывает, что поле удовлетворяется не во всей области (либо поверхности), а лишь в дискретном наборе точек.

Опыт проведения расчетов показывает, что при выборе достаточного числа точек может быть достигнута высокая точность решения. Однако точность решения зависит не только от числа точек , но и от их расположения. Этот метод достаточно прост и обеспечивает хорошую точность результатов для многих задач.

Кроме того-функции могут использоваться и в качестве базисных функций:

Это коллокационный метод нахождения приближенного решения задачи, сводящей ее к алгебраической задаче. Если взять М точек () и каждое из равенств спроецировать на оси декартовой системы координат, то количество уравнений будет .

В принципе можно взять и получить квадратную матрицу. Если окажется желательным при фиксированном усилить дискретизацию (увеличить ), то система уравнений окажется переопределенной, но и при этом можно получить решение.

Коллокационный подход применим и к интегральным уравнениям. Базис можно строить в виде набора гармоник см. рис.13.

Рис.13. Система гармоник.

Или его можно взять как набор констант, каждая из которых задана только на своем носителе см.рис.14.

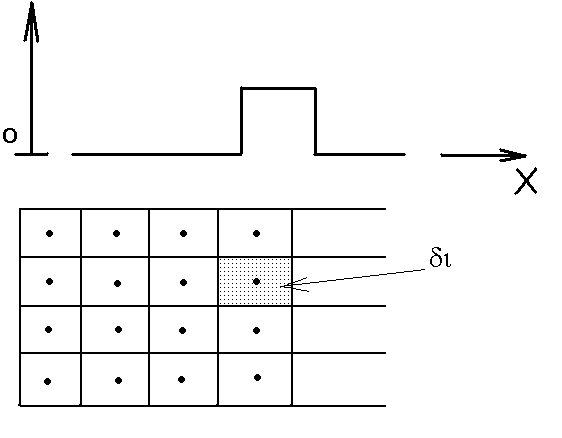
Рис.14. Система констант.

Применение такого базиса есть, по существу, реализация простейшего способа приближенного интегрирования.

Вместо проекционного положения граничных условий (метод Трефтца) возможно коллокационное; система точек при этом выбирается на нужной границе. В результате получается система уравнений относительно граничных значений компонент поля.

Коллокационные методы, будучи очень простыми, по замыслу, применяют еще довольно редко. Во-первых, оптимальный выбор коллокационых точек в каждом отдельном случае требует исследования. Во-вторых, они, вообще говоря, менее выгодны по сравнению с проекционными, которые в ряде случаев приводят к хорошим результатам при малых порядках системы алгебраических уравнений.

Разностные схемы. Сеточные методы

Пусть имеется равномерная координатная сетка в плоскости XOY c шагом h (см. рис 15).

Рис.15. Равномерная координатная сетка.

Приближенный метод решения краевой задачи можно построить так, чтобы решение рассматривалось только в узлах сетки, т.е. в точках с координатами , . Для этого все производные в формулировке задачи надо заменить их конечноразностными аналогами. Исходная задача сводится таким путем к системе линейных алгебраических уравнений посредством так называемой разностной схемы.

Рассмотрим кратко суть вопроса. Пусть нужно построить разностный аналог частотной производной по Х функции U(X,Y) в точке ,.

Рис.16.Разностная схема.

Значения U(,) будем кратко обозначать Um,n. Для производной

возможны правый аналог ℓпр и левый ℓл

;

.

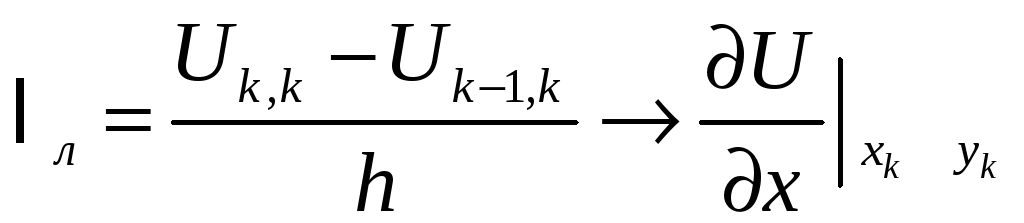Если теперь требуется построить вторую частную производную, то пишут

~

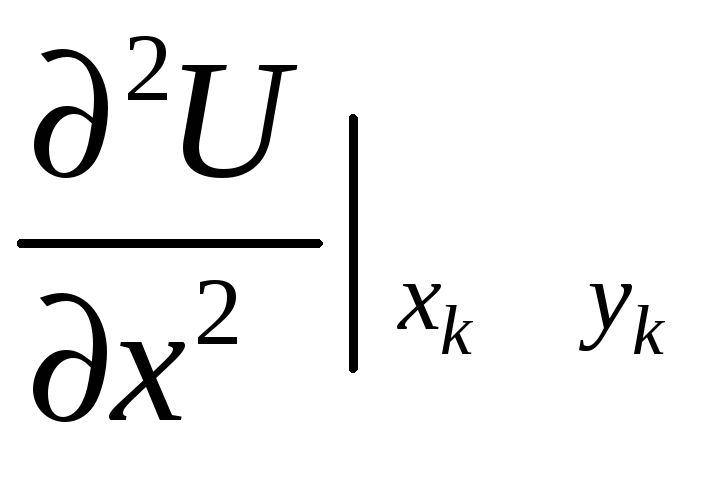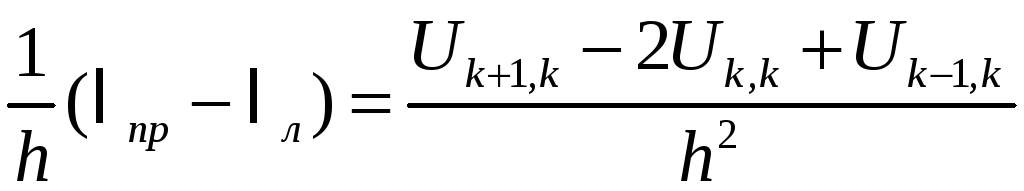
Совершенно аналогично строится производную .Поэтому для двумерного лапласиана имеет следующий разностный аналог:

~ ( 60 )

Поэтому, если, например, решается граничная задача

в S ,

U=0 на L,

где фигурирует уравнение Пуассона, то для некоторого узла сетки с номером (к,к) согласно ( 60 ) имеем

,

что дает систему линейных алгебраических уравнений, матрица которой будет очень разреженной. Для всех внутренних точек (независимо от числа узлов) количество отличных от нуля элементов матрицы в строке равно пяти.

Разностные схемы – распространенный метод алгоритмизации краевых задач. Поскольку аппроксимации подвергается дифференциальный оператор задачи, число узлов оказывается большим. Порядки систем алгебраических уравнений весьма высоки, по сравнению, например, с проекционными методами. Но разреженность матриц помогает в ряде случаев преодолеть эту трудность.

Для электродинамических задач разностные методы применялись относительно мало, что связано с рядом специфических трудностей. Иногда разносные схемы получают на основе уравнений Максвелла в интегральной форме. Поясним это на примере объемной равномерной координатной сетки (см. рис 16).

Рис.17. Объёмная равномерная координатная сетка (x= const).

Точка М(x,y,z), для которой составляются разностные соотношения, лежит в центре куба с ребром 2h. Возьмем уравнения Максвелла в интегральной форме:

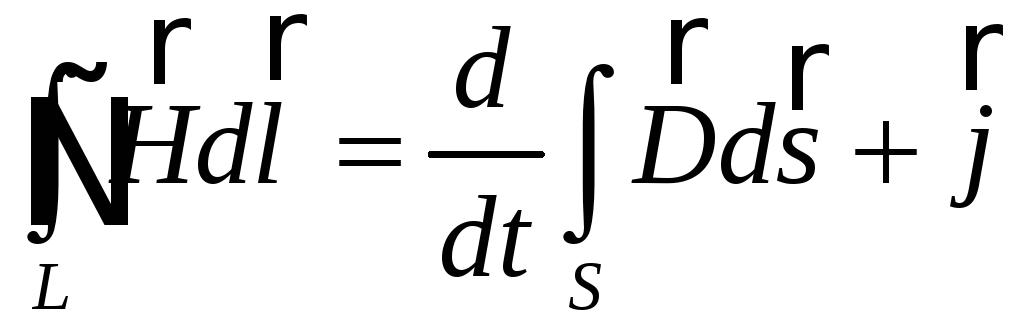( 61 )

( 62 )

В рамках метода комплексных амплитуд ( ) и заменяя на возьмем в качестве заштрихованное сечение куба плоскостью х=const; направление обхода его контура L показано стрелкой. При достаточно малом h из (62), приближенно следует:

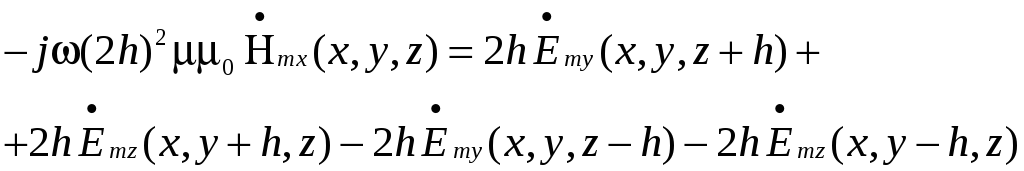
Или

аналогично из (61) получаем

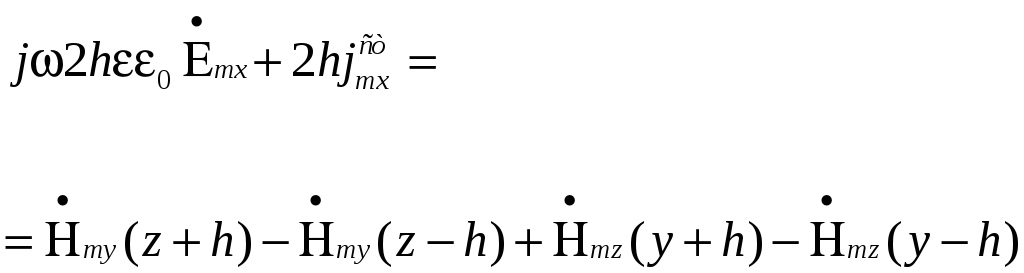
Чтобы достроить систему разностных соотношений нужно еще выполнить подобные же операции в плоскости y=const и z=const, проходящих через точку М(x,y,z).

Рис.18. Объёмная равномерная координатная сетка (z= const и y=const.).

Выполнив аналогичные операции, получим систему линейных алгебраических уравнений. Вопросы устойчивости и сходимости СЛАУ, полученных разностными методами хорошо разработаны. Однако порядок СЛАУ, необходимых для достижения хороших результатов очень высок.

Метод конечных элементов.

В процессе дискретизации можно строить представления решения в некоторых малых областях, называемых конечными элементами. При изложении метода коллокаций рассматривался пример, позволяющий говорить о применении простейших конечных элементов в виде носителей констант ; речь шла об алгоритмизации интегрального уравнения.

Обычно под методом конечных элементов, который называется также проекционно-сеточным, понимают процесс Бубнова-Галеркина для некоторой краевой задачи, в которой базис формируется из функций, определенных не во всей области задачи, а на специально построенной системе носителей.

Обсудим сущность метода. На рисунке показаны функции в виде констант:

Рис.19. Система носителей в виде констант.

(ср. с методом коллокаций)

По таким функциям ,можно было бы построить представление решения задачи

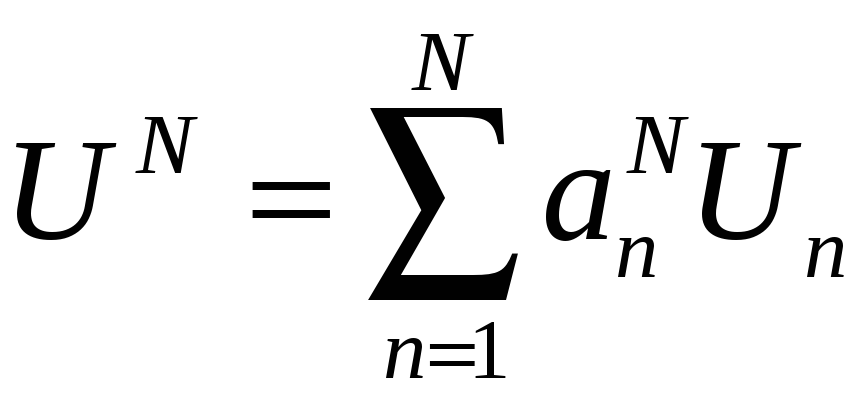
Если оператор -интегральный; выражение при этом имеет смысл. Если же выполняется операция однократного дифференцирования, то нужно, чтобы базисы функции были непрерывными. При этом конечно-элементное представление строится из функций-крышек, носители которых пересекаются.

Рис.20. Система носителей в виде функций-крышек.

Что дает метод конечных элементов в сравнении с обычным методом Бубнова-Галеркина, когда базисные функции определены во всей области задачи?

Главное- это разреженность матрицы в выражении ( 38 )

действительно отличны от нуля будут только те из элементов

,

которые образованы функциями- крышками соседних пересекающихся носителей.

Существуют разные способы построения конечных элементов на поверхности и в объеме. Часто используется треугольная сетка, удобная в частности в случае криволинейной границы.

Рис.21. Различные способы построения конечных элементов.

При этом базисные функции можно строить в виде

, ( 63 )

где константы однозначно связаны со значениями в узлах (вершинах треугольника). Совокупность всех узловых значений образует неизвестный вектор решения. Очень существенно, что представление в этом случае непрерывно. Представления типа ( 63 ) образуют линейные конечные элементы. Можно строить квадратичные элементы и элементы более высокой степени.

При алгоритмизации электродинамической задачи Е_n и H_n строятся так, что их координатные составляющие Е_nх ,Е_nу… имеют конечно элементное представление.