Применение метода Ритца к анализу свойств резонаторов

Рассмотрим резонатор простой формы, заполненный неоднородной анизотропной средой.

Для простоты будем предполагать, что параметры меняются непрерывно, а тензоры и Эрмитовы, т.е. для них справедливо:

.

Эрмитовы тензоры и соответствуют средам без потерь.

При решении поставленной задачи можно использовать уравнения в различной форме и, в частности, решать уравнения Максвелла. Для того, чтобы применить аппарат, который использовался выше, перепишем уравнения Максвелла в следующей форме

(45)

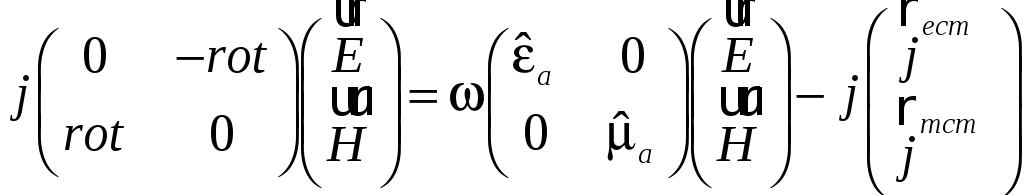
Эту запись надо понимать в смысле перемножения матриц на векторы столбцы.

Тогда уравнения Максвелла можно переписать в виде

,

где:

– «поле»; – «оператор Максвелла»; – «проницаемость»; – «источник».

Можно показать, что оператор Максвелла самосопряженный, если стенки резонатора идеально проводящие. Оператор Максвелла определен на векторах F, имеющих шесть составляющих – 3 Е-поля и 3 Н-поля.

Скалярное произведение функций F определяется как обычно

.

Тензоры диэлектрической и магнитной проницаемостей, каждый из которых имеет по девять составляющих, объединяются в один тензор «проницаемость» П, этот тензор имеет 36 составляющих. Вектор имеет шесть составляющих: три составляющих вектора и три . В дальнейшем для простоты положим .

Составим функционал

,

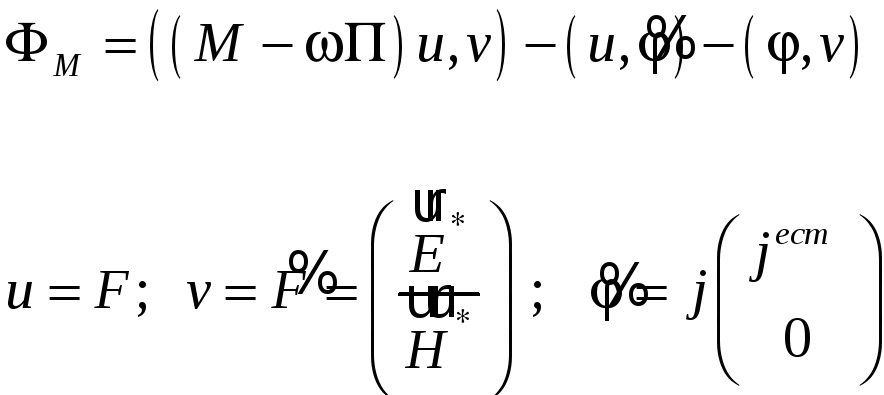Подставим в него

Тогда функционал примет вид

Здесь мы вновь перешли к обычной записи векторов поля. К этому функционалу применяется метод Ритца. В качестве координатных функций берутся собственные функции резонатора с однородным заполнением.

Функционал (46) позволяет построить алгоритм, а, следовательно, и программу для ЭВМ, пригодную для очень широкого круга заполнений резонатора анизотропной средой.

Недостатком этого метода является то, что координатные функции должны удовлетворять граничным условиям на поверхности резонатора. (Следовательно, резонаторы сложной формы рассматривать нельзя).

Описанный выше способ можно применять и для исследования не только резонаторов, но и нерегулярных волноводов. В технике при исследовании волноводных устройств, как правило, стремятся найти эквивалентную схему устройства в виде многополюсника. Многополюсник характеризуется либо матрицей рассеяния, либо матрицей проводимости (сопротивления). Определение элементов матриц обычно осуществляется с помощью нескольких опытов (в данном случае мысленных) короткого замыкания и холостого хода. Опыты КЗ и ХХ превращают волновод в резонатор, так что исследование волноводных устройств сводится к решению нескольких задач о возбуждении резонаторов, т.е. к решению рассмотренной выше задачи (так называемый метод стоячих волн).

Наиболее употребительные проекционные схемы в электродинамике.

Рассмотрев вводные методологические положения, перейдем к их конкретизации для задач электродинамики.

Возбуждение резонатора сторонним током .

Как мы уже говорили при равных условиях (Подразумевается тождественность решаемой задачи (моделируемого объекта) и функционального базиса ) процессы Бубнова – Галеркина и Ритца дают одну и ту же систему алгебраических уравнений.

Возьмем систему уравнений Максвелла:

(имеется сторонний ток, задача возбуждения)

Применим проекционную схему

:

:

В нашем случае

( 47)

где – основная область задачи, , принадлежат полным ортонормированным системам и .

Заметим, что пока еще решаемая задача не конкретизирована, для этого по крайней мере еще необходимо сформулировать краевые условия на поверхности , ограничивающей объем .

В качестве и в большинстве случаев удобно использовать системы собственных функций порождаемых следующей краевой задачей:

( 48 )

В простейшем случае объем совпадает с , но может быть частью .

Подчеркнем, что соленоидальные собственные функции (для которых и ) – это в данном случае собственные поля полого резонатора, а отвечающие им величины - соответствующие собственные (круговые) частоты. Имеются, однако, еще потенциальные собственные функции (, ); им всем отвечают собственные значения . Функции и ортонормируются в виде:

В методе Бубнова – Галеркина неизвестное решение задачи и представляется в виде:

(49)

;

Но прямая подстановка этих выражений в ( 47 ) не всегда допустима, т.к. это может привести к неверным результатам. Так как нет уверенности в возможности почленного дифференцирования (т.е. применения операции rot) по отношению к ортогональным рядам, в которые переходят представления ( 49 ).

Указанную трудность можно обойти: возьмем первый интеграл в ( 47 )

применим к нему тождество

,

Тогда

подставим

из ( 48 ).

После подстановки получим

Окончательно получим

( 50 )

Сюда и вносятся представления (49) после чего уравнение превращается в систему алгебраических уравнений.

Метод поперечных сечений.

Под этим наименованием подразумевается подход, при котором представления полей и проекционные соотношения строятся на виртуальном сечении (мысленно перемещаемом внутри объема ). Это поперечное сечение не обязательно является плоским. Если – ортогональная к координата, то поперечное сечение, вообще говоря, параметрически зависит

от .

.

На рис.2 это иллюстрируется в двух вариантах:

Рис.2 Виртуальные сечения в цилиндрической и сферической системах координат.

плоское ()

и сферическое ().

В (49) базисные функции и заменяются такими, которые определены на (обозначим их и ), а коэффициенты представлений становятся функциями координаты . Таким образом:

;

(51)

проекционная форма (47) заменяется следующей

В случае плоского поперечного сечения можно записать

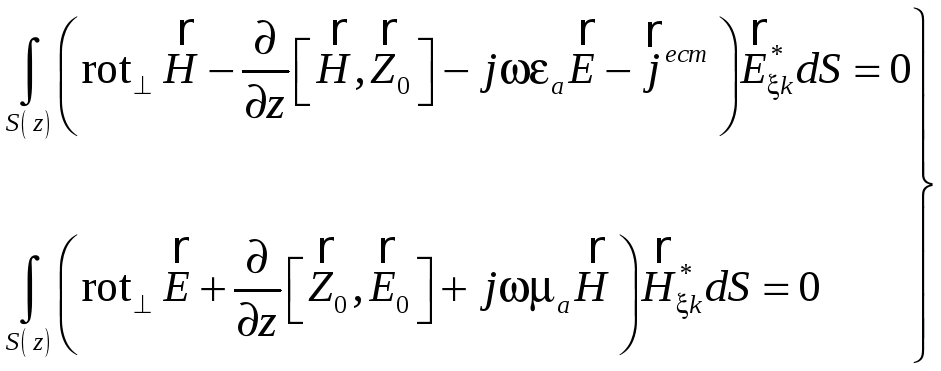
Здесь дифференцирование по продольной координате выделено, символ

означает дифференцирование по координатам поперечного сечения.

После преобразования путем дифференцирования по частям получается аналог (50). Но после подстановки (51) получается не система алгебраических уравнений, а система обыкновенных дифференциальных уравнений относительно коэффициентов и ().

Метод поперечных сечений иногда называется «неполный метод Бубнова – Галеркина».