Некоторые сведения из функционального анализа. Функционалы и операторы в гильбертовом пространстве

Общие свойства решения электродинамических задач, а также многие частные вопросы становятся более понятными и ясными, если воспользоваться некоторыми начальными понятиями из функционального анализа.

Рассмотрим множество каких-либо элементов, например скалярных или векторных функций, заданных в ограниченной области V. Выберем из этого

множества два элемента и и образуем сумму

где a и b — произвольные комплексные числа. Если сумма принадлежит к тому же множеству, то такое множество называется линейной системой.

Каждому элементу линейной системы можно поставить в соответствие число, называемое нормой, или каждым двум элементам — число, называемое (внутренним) скалярным произведением. После введения нормы линейная система превращается в нормированное пространство, а после введения скалярного произведения — в унитарное пространство. Скалярное произведение и норма могут вводиться различным образом, важно только чтобы они удовлетворяли определённым аксиомам. Введём (внутреннее) скалярное произведение (наиболее часто применяемый вид) в виде:

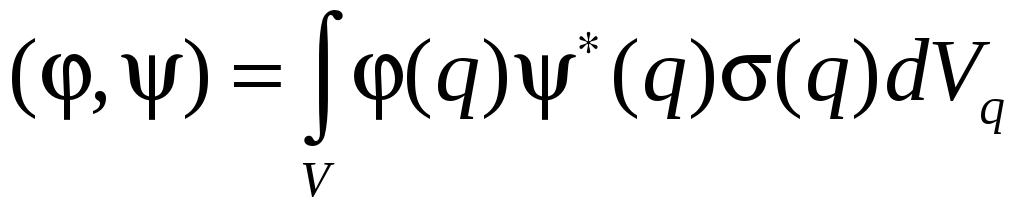(30)

— знак комплексного сопряжения;

— неотрицательная функция, обращающаяся в нуль только в отдельных изолированных точках. Она называется весовой функцией.

Корень квадратный из скалярного произведения функции самой на себя определяется как норма

(31)

т.е. унитарное пространство в тоже время является нормированным.

Важнейшим является понятие полноты пространства. Оно связано с определением фундаментальной последовательности элементов (функций) , т.е. бесконечной последовательности (n меняется от 1 до ∞), удовлетворяющей условию

Если всякая фундаментальная последовательность имеет предел в рассматриваемом пространстве, т.е. во всех случаях предельная функция принадлежит к тому же пространству, то такое пространство называется полным.

Полное унитарное пространство носит название пространства Гильберта, а полное нормированное пространство – пространство Банаха. Пространство Гильберта со скалярным произведением в приведенной выше форме, элементами которого являются функции с интегрируемым квадратом, называется пространством (в частном случае может равняться 1). То же пространство является пространством Банаха. Нетрудно видеть, что пространство является естественным обобщением n-мерного евклидова пространства на бесконечномерный случай.

Рассмотрим теперь определение функционала и оператора, ориентируясь на гильбертово пространство. Если каждому элементу φ из множества , принадлежащему Гильбертову пространству, поставлено в соответствие число, то тем самым на множестве задан функционал .

Функционал является линейным, если

Он ограничен, если для любого элемента из множества функционал удовлетворяет неравенству

Наименьшее число N в неравенстве называют нормой функционала и обозначают Можно показать, что всякий ограниченный линейный функционал можно представить в виде скалярного произведения данного элемента и некоторого фиксированного элемента U, т.е. всякий ограниченный функционал в , представляется интегралом

,

где U(q) – некоторая фиксированная функция из .

Если каждому элементу из множества по некоторому закону поставлен в соответствие один и только один элемент из области , то говорят, что задан оператор .

Принято записывать

( 32 )

Множество носит название области определения оператора, а область всевозможных значений называется областью значений оператора.

Область определения оператора входит в определение оператора. По существу, область определения оператора связана с граничными условиями, налагаемыми на функции . Именно граничные условия определяют класс функций , а, следовательно, область определения оператора.

Оператор называется линейным, если

Оператор ограничен, если для любого элемента из

Наименьшее из чисел называется нормой оператора.

С помощью равенства

ограниченному оператору ставится в соответствие сопряженный оператор . Предполагается, что область определения операторов и все пространство . Если операторы и совпадают, то они называются самосопряженными. Следует подчеркнуть, что в случае дифференциального оператора для самосопряженности необходимо, чтобы у исходного и сопряженного операторов совпадали дифференциальное выражение и область определения, т.е. граничные условия.

Важнейшими понятиями являются понятия собственной функции и собственного значения оператора. Они определяются равенством

пример:

т.е. собственные функции оператора – это функции, которые преобразуются оператором в себя с некоторым множителем , именуемым собственным значением.

Совокупность собственных значений называется спектром оператора.

Известно, что собственные значения самосопряженного оператора действительны. Если область определения функций ограничена, то спектр собственных значений дискретный и образует счетную последовательность.

Собственные функции самосопряженного оператора образуют полную ортогональную систему функций. Для удобства системы собственных функций принято нормировать, т.е. делить каждую функцию на ее норму. Такие системы называются ортонормированными.

Они удовлетворяют условию:

Полнота системы функций в определенном классе означает, что любая функция из этого класса функций, может быть разложена в ряд по этой системе функций.

Например, если под областью понимать отрезок числовой оси , то на нем в полна система гармоник в виде синусов и косинусов. Если выделить из класс четных функций, то будет полна система гармоник в виде косинусов (нечетных – синусов).

При решении внутренних задач приходится иметь дело с оператором Лапласа , входящим в уравнение Гельмгольца, а также аналогичными. Можно показать, что при отсутствии потерь в стенках волноводов и резонаторов все они являются самосопряженными.

Собственные функции во внутренних задачах имеют наглядный физический смысл собственных колебаний в резонаторах и собственных волн в волноводах. Полнота системы собственных функций позволяет любое поле представить в виде разложения по собственным колебаниям или собственным волнам.