Проекционные методы Ортогональные ряды и проекционная интерпретация.

Пусть некоторая функция U, определенная в области , разлагается в ортогональный ряд (ряд Фурье) по полной ортонормированной системе . Это значит, что ищутся коэффициенты представления

( 33 )

( – есть обозначение для ряда Фурье функции U).

Введем скалярное произведение ( 30 )

(вес )

Если , то говорят, что функции U и V ортогональны.

Ортонормированная система есть совокупность таких функций что

, – символ Кронекера.

Для ряда Фурье необходимым является выполнение равенства

Подставим

,

так как

то ( 34 )

Для уяснения сущности разложения Фурье рассмотрим следующую иллюстрацию.

Пусть в трехмерном пространстве выбрана декартова система координат, и, следовательно, имеются три единичных взаимно перпендикулярных вектора

.

Рис.1 Разложение вектора по осям в декартовой системе координат.

Если в рассматриваемом трехмерном пространстве задать произвольный вектор , то его можно представить в виде:

(3)

, ( 35 )

где

- есть не что иное, как проекция вектора на ортогональные направления, которым отвечают векторы , т.е. направления .

Вектор теперь представлен при помощи трех своих проекций , являющихся скалярными произведениями вектора на единичные базисные векторы , подчиненным соотношением .

Сопоставляя два равенства ( 33 ) и ( 35 ) замечаем отчетливую формальную аналогию между построчным разложением вектора и рядом Фурье функции U. Разлагаемая функция подобна вектору в бесконечномерном пространстве, а ее ряд Фурье можно рассматривать как разложение этого вектора в базисе, (или проектируемый на «направления») образованном ортонормированной системой .

Пример: Ряд Фурье

.

необходимо в приведенных выше терминах рассматривать, как ряд Фурье, получаемый при разложении функций U(t), определенной на отрезке

по ортонормированной системе

Проекционный метод Бубнова-Галеркина (1913 – 1915 г.г.)

В основе проекционных методов лежит стремление искать решение задачи при помощи операций, прямо или косвенно связанных с проектированием в функциональном Гильбертовом пространстве.

Поставленную задачу кратко сформулируем в виде

, ( 36)

где А – некоторый оператор задачи, например, дифференциальный (с заданием краевых условий), интегральный либо иной; будем полагать его линейным. В правой части заданная функция f, выражающая обычно фактор возбуждения исследуемого объекта («вынуждающая сила»). Символом U обозначено неизвестное решение задачи.

Рассмотрим тождественно равную нулю функцию

.

Разлагая ее в ряд Фурье, мы должны получить все коэффициенты Фурье равными нулю. Взяв систему и, пользуясь правилом вычисления коэффициентов Фурье, имеем

Приближенное решение задачи будем искать в виде ортогонального представления

, (37)

(верхний индекс N характеризует число членов суммы), где коэффициент – некоторые неизвестные величины; систему N функций будем называть базисом процесса Бубнова-Галеркина. Будем считать, что для каждой базисной функции имеет смысл выражение ( – принадлежит области определения оператора А , или кратко: ). Тогда подставляя вместо U получим

Подставим в последнее выражение

( 38 )

Раскроем это, например, для k=1; n=1,2…N

Т.е. имеем неоднородную систему линейных алгебраических уравнений относительно коэффициентов , как неизвестных.

Или в краткой форме:

, ( 39)

где – вектор коэффициентов (столбец чисел ); – матрица с элементами , а в правой части вектор с коэффициентами .

Таким образом, метод Бубнова – Галеркина сводит поставленную задачу к системе линейных алгебраических уравнений.

Решение уравнения ( 39 ) может быть получено с помощью стандартных методов обращения матриц. В результате получаем вектор столбец

Говорят, что процесс Бубнова – Галеркина сходится, если в пределе при представление

.

Если это ожидание оправдывается, то говорят, что процесс Бубнова – Галеркина сходится к решению задачи.

Обычно при этом

,

где – коэффициенты Фурье решения U задачи. Следует подчеркнуть, что вообще .

Строгое доказательство сходимости метода Бубнова – Галеркина для того или иного класса задач и для класса функций может оказаться трудной проблемой.

Значительный интерес представляют задачи на собственные значения. Обычно в этом случае фигурирует объект при отсутствии внешних воздействий. Полагая в исходной задаче

,

где λ – параметр, а q- «оператор веса» (чаще всего некоторая функция или константа), запишем

– уравнение Гельмгольца

(пример ).

Задачи на собственные значения имеют серию решений , которые реализуются при соответствующих значениях параметра . По определению, – собственные функции, а отвечающие им – собственные значения задачи. И те, и другие подлежат определению при решении задачи.

Применяя метод Бубнова – Галеркина имеем

.

(Символ – означает приближенное значение , которое будет получено при проведении процесса Бубнова – Галеркина).

Далее, подставив , получим

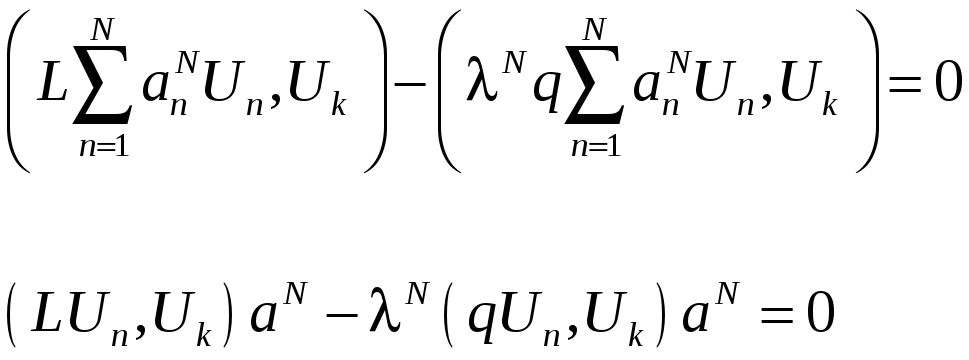
или в матричном виде:

(40)

,

где матрицы имеют элементы

.

Из условия совместности системы (определитель = 0)

получаем характеристическое уравнение относительно (алгебраическое уравнение степени N). Его корни При решении системы (40) находим отвечающие этим приближениям векторы , а внося их в разложение получаем собственные функции