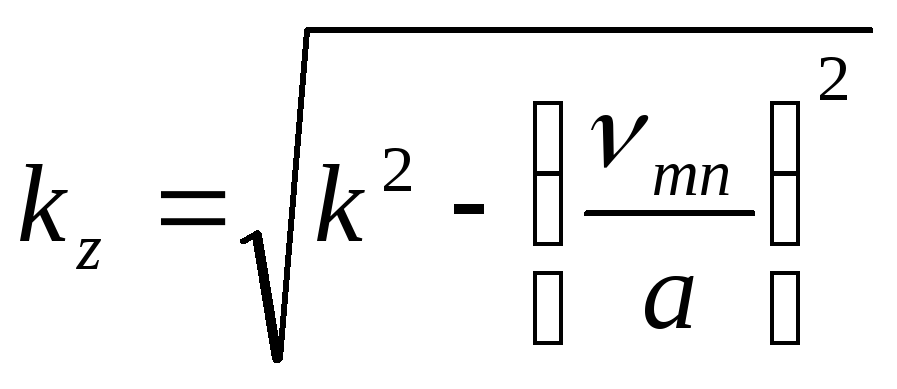- •Типы эл м волн и полей
- •2.Понятие о критическом угле паления при отражении радиоволн
- •Свойства волн типа т
- •2.Понятие о полюсно и линейно поляризованной волне
- •Свойства волн е и н типа
- •2.Понятие о круговой поляризации эл. М волн
- •Характерные особенности поверхностных электромагнитных волн
- •2. Критическая длинна волны в волноводах
- •Общие свойства поверхностных волн е и н типа
- •2.Решение волнового уравнения для поля магнитных волн в круговом волноводе
- •Билет №6
- •1 Вопрос Выбор размеров прямоугольного волновода для основного типа волны.
- •2 Вопрос Резонансная длина волны круглых резонаторов. Резонансная частота объемного резонатора.
- •Билет №7
- •1 Вопрос Диаграмма направленности элементарного электрического вибратора.
- •2 Вопрос Графическая зависимость коэффицентов Фрэнеля от угла падения плоской волны.
- •Билет №8
- •1 Вопрос Электрические волны в круглом волноводе.
- •2 Вопрос
- •Отражение плоских волн на границе идеальных диэлектриков.
- •Билет №9
- •1 Вопрос Краевая (граничная) задача для волноводов.
- •2 Вопрос Резонансная длина волны прямоугольног резонатора. Резонансная частота объемного резонатора.
- •Билет №10
- •1 Вопрос Переход от волноводов к объёмным резонаторам.
- •2 Вопрос
- •Билет 12 Закон Брюстера
- •2.Решение краевой (граничной) задачи в прямоугольном волноводе.
- •2. Режим работы волновода.
- •Распространение эл м волн в анизотропных средах.
- •2.Распространение плоской однородной волны в феррите вдоль подмагничевающего поля. Эффект Фарадея
- •Билет 17 1. Поверхностные волны над ребристой периодической металлической структурой.
- •2. Коэффициент затухания и кпд линии передач.
- •Уравнение связи
- •Билет №21.
- •1 Вопрос:”Понятие поля. Физическое поле. Виды полей”.
- •2 Вопрос:”Связь векторов поля с электрическими потенциалами”.
- •Билет №22
- •1 Вопрос:”Электрические заряды. Распределение зарядов. Плотность зарядов”.
- •Линейная плотность заряда[кул/м].
- •Принцип суперпозиции.
- •2 Вопрос: ”Интегральные теоремы Остроградского-Гаусса и Остроградского-Стокса”.
- •Билет №23
- •1 Вопрос:”Электрические токи. Сила тока и плотность тока”.
- •Объёмное распределение токов.
- •Поверхностное распределение токов.
- •Линейная плотность тока.
- •2 Вопрос:”Вектор Умова-Пойтинга. Среднее его значение за период”.
- •Билет №24.
- •1 Вопрос:”Полная система уравнений электродинамики”.
- •2 Вопрос:”Понятие о плоской однородной волне”
- •Теорема Умова-Пойтинга
- •Переход из интегральной формы к дифференциальной.
- •1.Закон электромагнитной индукции.
- •Вопрос 1. Третье уравнение электродинамики. Теорема о потоке вектора магнитной индукции.
- •Вопрос 2.
- •Вопрос 1. Четвёртое уравнение электродинамики. Теорема о потоке вектора электрическойой индукции.
- •Вопрос 2.
- •Вопрос 1.
- •Вопрос 2. Плоская однородная волна в среде с потерями.
- •Вопрос 1.
- •Вопрос 2. Плоская однородная волна в среде с потерями.
- •Вопрос 1.
- •Сопротивление проводников при поверхностном эффекте.
- •Вопрос 2.
2. Критическая длинна волны в волноводах
Рассмотрим коэфицент
распространения
![]() в задачах о волноводах.
в задачах о волноводах.
Нетрудно видеть,
что этот коэфицент может принимать
различные значения (![]() быть
мнимым) в зависимости от параметров
среды, заполняющей трубу, и типа
распространения волны, и размеров
волновода.
быть
мнимым) в зависимости от параметров
среды, заполняющей трубу, и типа
распространения волны, и размеров
волновода. ![]()
Е![]() сли
сли
![]() ,
то все составляющие будут помножаться
на
,
то все составляющие будут помножаться
на
![]()
Если
![]() ,
то все составляющие будут пропорциональны
,
то все составляющие будут пропорциональны
![]()
![]()
(поле колеблется в поперечном сечении волновода, не распространяясь)
Между этими случаями
есть граница: ![]()
О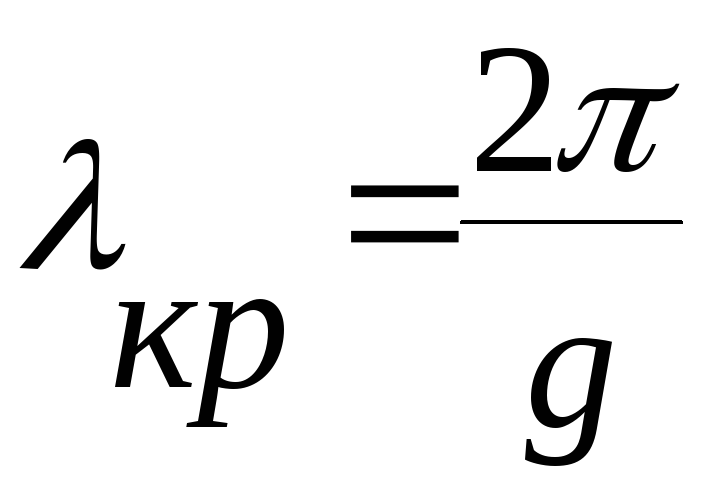 чевидно,
чевидно,
![]() .
Раз существует
.
Раз существует
![]() ,
то -
критическая
длина волны
,
то -
критическая
длина волны
Таким образом,
![]() -
такая длина волны, длиннее которой
электромагнитная энергия не может
распространяться по волноводу.
-
такая длина волны, длиннее которой
электромагнитная энергия не может
распространяться по волноводу.
Например:
П![]()
 рямоугольный
волновод: Круглый волновод:
рямоугольный
волновод: Круглый волновод:
![]()
![]()
![]()
![]() для
Н-волн
для
Н-волн
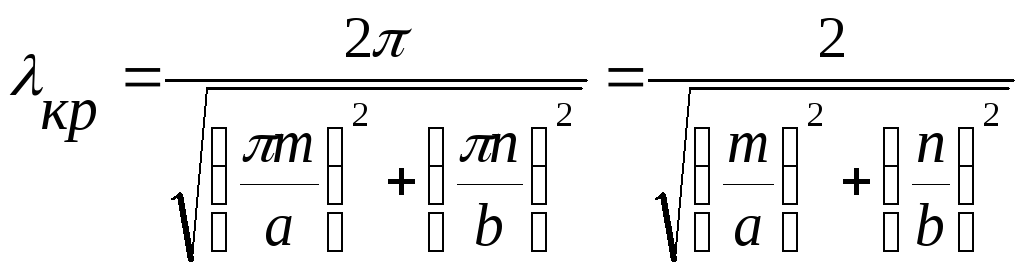
![]()
![]() для
Е-волн
для
Е-волн
![]()
![]() Нетрудно
видеть из выражений для , что, чем выше
Нетрудно
видеть из выражений для , что, чем выше
![]() (индексы
(индексы
![]() и
и
![]() )
при заданных размерах волновода, тем
меньше ,следовательно, нам будет
труднее выполнить неравенство
)
при заданных размерах волновода, тем
меньше ,следовательно, нам будет
труднее выполнить неравенство
![]() (условие
распространения).Его можно выполнить
при больших
(условие
распространения).Его можно выполнить
при больших
![]() и
и
![]() только увеличивая размеры волновода,
а это не выгодно на практике. Поэтому
на практике стараются работать с
наинисшими типами волн (на меньших
только увеличивая размеры волновода,
а это не выгодно на практике. Поэтому
на практике стараются работать с
наинисшими типами волн (на меньших
![]() и
и
![]() ),
чтобы обеспечить минимальные размеры
волновода. Для прямоугольного волновода
таким наинисшим типом волн (основным)
является волна
),
чтобы обеспечить минимальные размеры
волновода. Для прямоугольного волновода
таким наинисшим типом волн (основным)
является волна
![]() (для
этой волны получаются и наименьшие
потери) Для круглого волновода основным
типом волн является для волн типа Н
волна
(для
этой волны получаются и наименьшие
потери) Для круглого волновода основным
типом волн является для волн типа Н
волна
![]()
![]() ,
для волн типа Е волна
,
для волн типа Е волна
![]()
![]()
Билет 5
-
Общие свойства поверхностных волн е и н типа
Пусть вдоль замедляющей структуры распространяется эл\м поверхностная волна Е- или Н- типа.
Пусть в направлении оси Х она бесконечно протяженная.

Любая составляющая
поля:
![]()
Рассмотрим уравнения электродинамики:
![]() (1)
(1) ![]() (2)
(2)
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() (3)
(3)
Из (1),(2) с учетом (3) получим:
![]() (2а)
(2а)
![]() (1б)
(1б)
![]() (1в)
(1в)
![]() ,
,
![]() подставим в (2а)
подставим в (2а)
![]()
![]()
![]()
Раз есть продольная составляющая вектора поля,
то есть и продольная составляющая вектора Умова-Пойтинга.
Примем за положительное направление составляющей вектора Пойтинга направление из первой среды во вторую, тогда для сопротивления поверхности можно написать:
![]()
Импеданс:
![]() ,
волновое число:
,
волновое число:
![]()
![]()
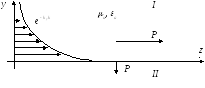
![]()
Любая составляющая
поля:
![]()
Рассмотрим уравнения электродинамики:
![]() (1)
(1) ![]() (2)
(2)
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() (3)
(3)
Из (1),(2) с учетом (3) получим:
![]() (1а)
(1а)
![]() (2б)
(2б)
![]() (2в)
(2в)
![]() ,
,
![]() подставим в (1а)
подставим в (1а)
![]()
![]()
![]()
![]()
![]()
Импеданс:
![]() ,
волновое число:
,
волновое число:
![]()
Из рассмотрения Е- и Н- волн, сделаем выводы:
Таким образом, из полученных выражений следует, что импеданс направления оси Y не зависит от координаты y (одинаков по всей оси Y). Это значит, что импеданс поверхностной волны мы можем считать импедансом поверхностной структуры при у=0.
Тогда из полученных
выражений следует, что при
![]() (условие экспоненциального спадания
поля по оси Y)
импеданс для Е-волн должен носить
индуктивный характер, а для Н-волн –
емкостной характер.
(условие экспоненциального спадания
поля по оси Y)
импеданс для Е-волн должен носить
индуктивный характер, а для Н-волн –
емкостной характер.
2.Решение волнового уравнения для поля магнитных волн в круговом волноводе
Для нахождения поля необходимо решать уравнение электродинамики. Запишем их в цилиндрической системе координат:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Будем искать поле
внутри трубы в виде волн, бегущих вдоль
оси z.
Если труба бесконечно длинная, то
отражение происходит в сторону
положительного направления оси z,
то все множители будут пропорциональны
![]() .
Зависимость от z
нам известна, можем взять производные.
.
Зависимость от z
нам известна, можем взять производные.
(1)
![]() (4)
(4)
![]()
(2)
![]() (5)
(5)
![]()
(3)
![]() (6)
(6)
![]()
Из уравнений (1)(2)(4)(5) можно выразить все Из (3) и (6) получим выражения для
поперечные составляющие через продольные: продольных составляющих волн:
![]() (7)
(7)
![]() (11)
(11)
![]() (8)
(8)
![]() (12)
(12)
![]() (9)
(9)
![]()
![]() (10)
(10)
Система уравнений
(7)-(12) показывает, как и в прямоугольном
волноводе, принципиальную возможность
распространения вдоль круглого волновода
одновременно Е- и Н- волн.Система (7)-(12)
линейна. Как и ранее, она может быть
представлена в виде двух линейных
систем, каждая из которых получается
из (7)-(12) путем поочередной подстановки
сначала
![]() ,
а затем
,
а затем
![]() .
.
![]() : Н-волны
: Н-волны
![]() : Е-волны
: Е-волны
![]()
![]()
![]()
![]()
![]() (13)
(13)
![]() (14)
(14)
![]()
![]()
![]()
![]()
Найдем решение для магнитных волн (системы (13)).
Искомое решение
находится по методу разделения переменных:
![]()
![]()
![]()
![]()
![]()
Слева функции
только переменной R,
справа функция только переменной Ф,
равенство может выполняться только
тогда, когда каждая из частей постоянна.(![]() )
)
1![]() 4
4![]()
2![]()
![]()
![]()
3![]() 5
5![]() Уравнение
Бесселя
Уравнение
Бесселя
Это уравнение не решается с помощью обыкновенных тригонометрических функций. Решения записываются с помощью специальных цилиндрических функций.
![]() ,
где
,
где
![]() - цилиндрические функции, которые
табулированы.
- цилиндрические функции, которые
табулированы.
![]() - цилиндрическая
функция первого рода (функция Бесселя)
- цилиндрическая
функция первого рода (функция Бесселя)
![]() -
цилиндрическая функция второго рода
(функция Неймана)
-
цилиндрическая функция второго рода
(функция Неймана)
Построим графики этих функций:
Общее решение для
![]()
![]()
![]()
Решение должно
подчиняться граничным условиям:
![]()
![]()
![]()
![]()
Выберем начало
координат: пусть
![]() при
при
![]()
Очевидно, при
![]() ,
,
![]() поле должно быть однородным.
поле должно быть однородным.
При
![]()
![]() конечно, но функция
конечно, но функция
![]() при
при
![]() бесконечна, следовательно,
бесконечна, следовательно,
![]() .
.
П![]() олучили:
олучили:
![]()
Наше решение должно подчиняться граничным условиям:
![]()
![]() Это уравнение
имеет бесчисленное множество корней.
Это уравнение
имеет бесчисленное множество корней.
![]()
![]() -порядок
функции,
-порядок
функции,
![]() -номер
корня
-номер
корня
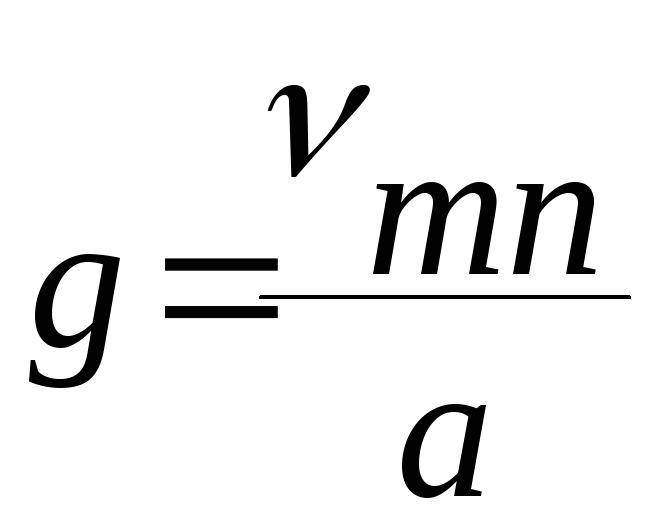
Мы получили
![]()
По системе (13) вычислим поперечные составляющие:
![]()
![]()
![]()
![]() Коэфицент
распространения:
Коэфицент
распространения:
![]() ,
,
![]()