Уравнение связи
Теперь:
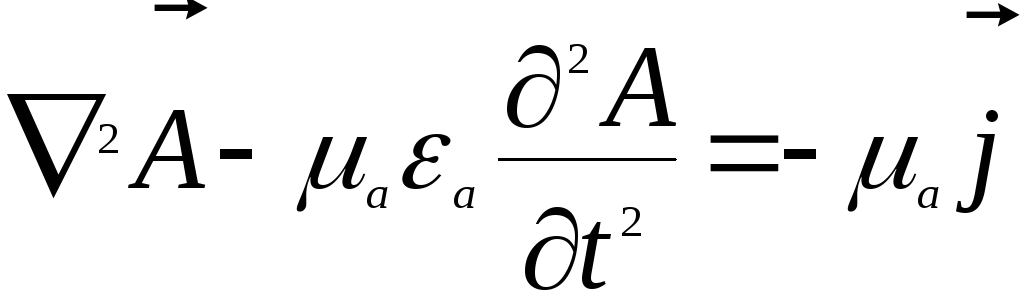
Рассмотрим 4 уравнение:
-div
div
-
-
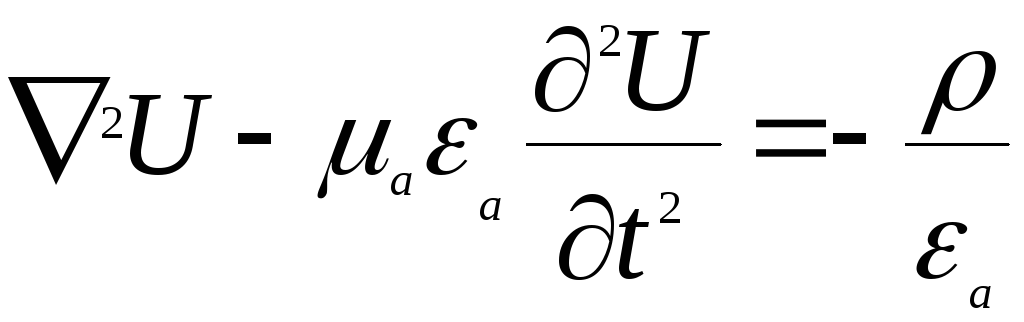
Получим неоднородные волновые уравнения для этих вспомогательных функций, методы решений которых достаточно математически развиты.
Вспомогательные величины
и U называются
вспомогательными электродинамическими
потенциалами.
- векторный электродинамический
потенциал
U – скалярный электродинамический потенциал
(частный случай
)
Билет №21.
1 Вопрос:”Понятие поля. Физическое поле. Виды полей”.
Электромагнитное поле есть особый вид материи, отличающийся непрерывным распределением в пространстве (электромагнитные волны, поле заряженных частиц) и обнаруживающий дискретность структуры (фотоны), характеризующийся в свободном состоянии способностью распространения в вакууме (при отсутствии сильных гравитационных полей) со скоростью, близкой к скорости света (3*108м/с) и оказывающий на заряженные частицы силовое воздействие, зависящее от их скорости.
Кроме отмеченной материалистической трактовки поля различают физическое и математическое понятие поля.
С физической точки зрения, поле есть некоторое непрерывное распределение физических свойств материи в пространстве и времени (поле давления, зарядов и т.п.).
Для описания физического поля вводится
понятие математического поля. Для
этого в каждой точке пространства,
занятого физическим полем, вводиться
соответствующая математическая величина
в виде функции координат этой точки и
времени:
.
Таким образом, математическое поле есть
непрерывная система функций координат
и времени. Иными словами математическое
поле есть удобная математическая
интерпретация физической ситуации
непрерывно распределённой в пространстве
и времени.
С математической точки зрения различают поля по характеру физической величины:
-
Скалярные – это такие поля, для описания которых значения функции каждой точки пространства требуется только числа (поле температур, поле давлений…)
-
Векторные – это такие поля, в которых значения функции требуют для своего определения не только величины, но и направления. Эти поля определяются заданием в каждой точке пространства и времени трёх скалярных величин – трёх проекций вектора ( электрическое поле…)
-
Тензорные – эти поля требуют для своего определения в каждой точке 9 скалярных величин, каждая из которых функция координаты и времени (электромагнитное поле в анизотропной среде…)
С математической точки зрения различают поля по характеру зависимости от времени:
-
Статические (постоянные) – независящие от времени
-
Динамические (переменные) – зависящие от времени
-
Стационарные – это поля, установившегося во времени движения
С математической точки зрения различают поля по характеру зависимости от координат:
-
Трёхмерные (пространственные) – функции зависят от
-
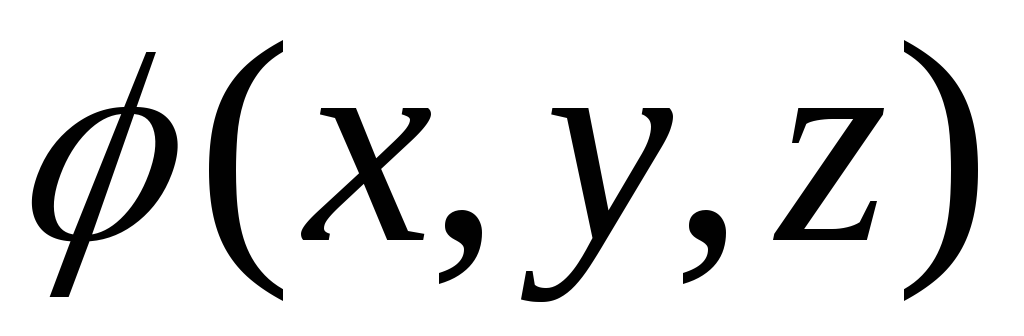
Двумерные (плоские) – функции зависят от
-
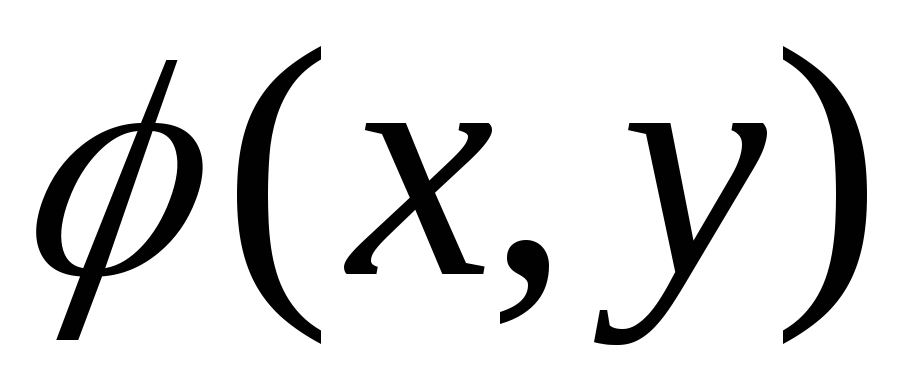
Одномерные – функции зависят от
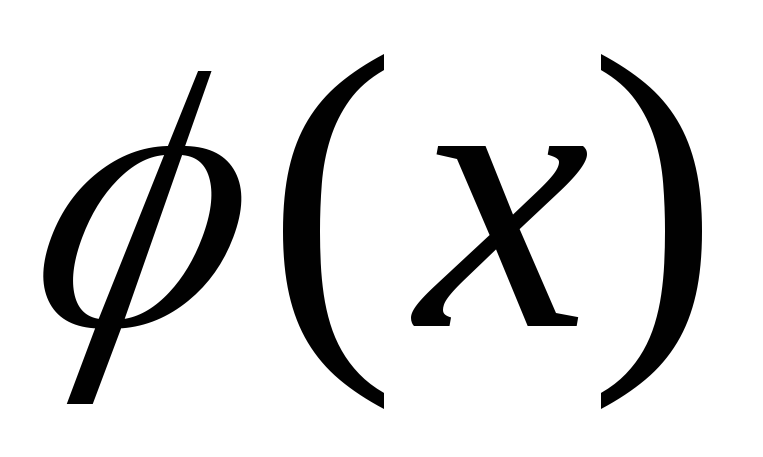
Математический характер поля определяется сущностью соответственного физического поля.
Материи (среды – вещества), в которых мы будем изучать электромагнитные явления.
-
Они могут быть безграничными или занимать конечную часть пространства.
-
Будем различать однородные и неоднородные среды.
Среда называется однородной, если
параметры среды везде или в данной части
пространства не изменяются, т.е. не
зависят от координат
В противном случае среда будет неоднородной.
-
Вакуум является особой средой, но он материален. Он не содержит обычных корпускулярных видов материи, но он не пуст, его заполняют различные физические поля.
-
Будем различать анизотропные и изотропные среды.
Среда называется изотропной, если
взаимодействие поля со средой не зависит
от направления его приложения
,
а для анизотропной среды любая
координата
Анизотропные среды характеризуются тензорными параметрами.
-
Будем различать линейные среды и нелинейные.
Среда называется линейной, если в ней параметры, её характеризующие не зависят от интенсивности приложенного поля. Всегда является линейной, как правило, при малых интенсивностях. Для линейной среды справедлив принцип суперпозиции.
Нелинейность среды проявляется при больших полях и заключается в зависимости параметров среды от интенсивности поля.