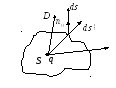
Вопрос 1. Четвёртое уравнение электродинамики. Теорема о потоке вектора электрическойой индукции.

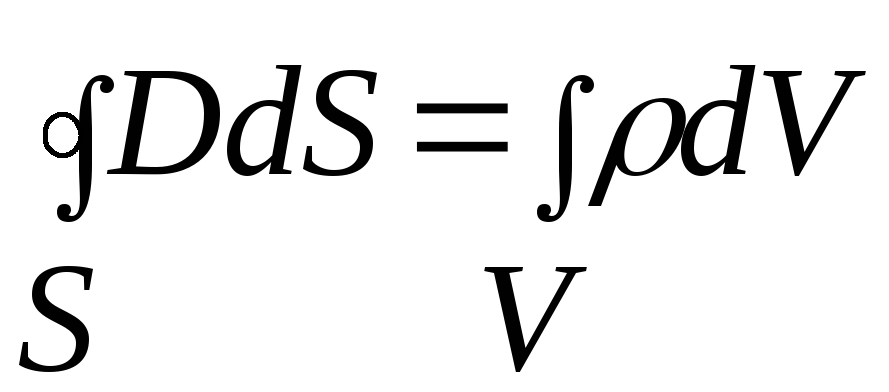
Поток вектора электрической индукции сквозь произвольную замкнутую поверхность равен полному заряду, находящемуся внутри её.

- телесный угол

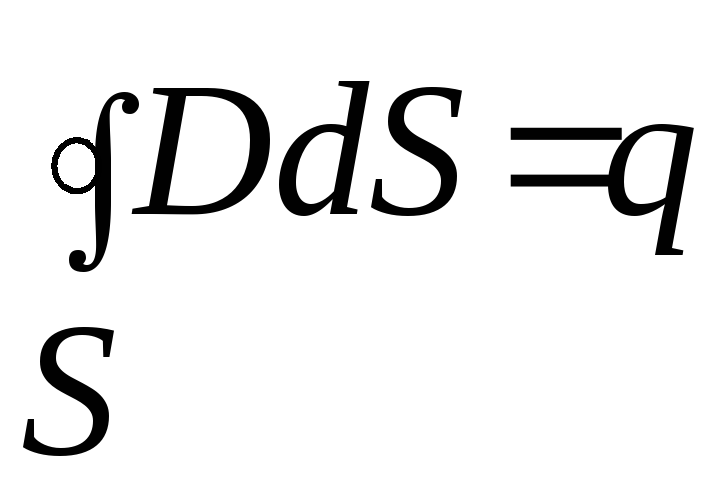
Если заряд объёмно распределён, то , воспользовавшись теоремой Остроградского – гаусса, получили:

Физический смысл: истоком вектора электрической индукции в каждой тоске пространства является объёмная плотность заряда.

Вопрос 2.

Решение уравнений электродинамики.

Система уравнение электродинамики является системой векторных дифференциальных уравнений. (нам неизвестны вектора H,E,∂, B и их проекции)

Способы вычисления (решения): их много, рассмотрим: - приведение этих уравнений к волновым уравнениям, методы решения которых достаточно хорошо развиты.Запишем решения для однородного, изотропного, безграничного пространста.

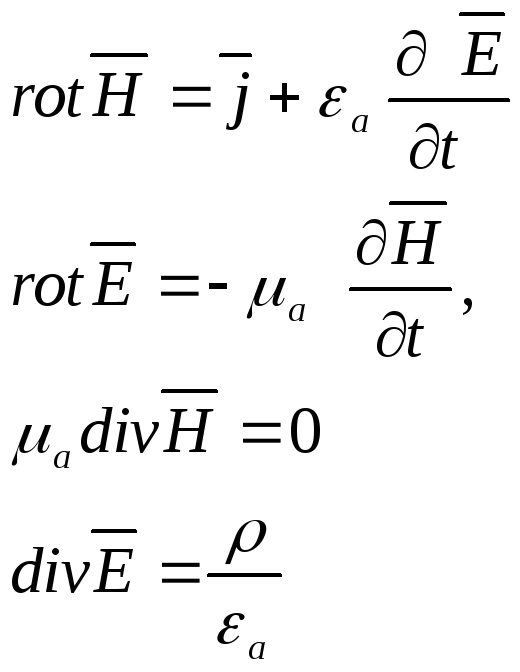
I. Умножим 1 на μ_а и продифференцируем:

Возьмем rot от 2

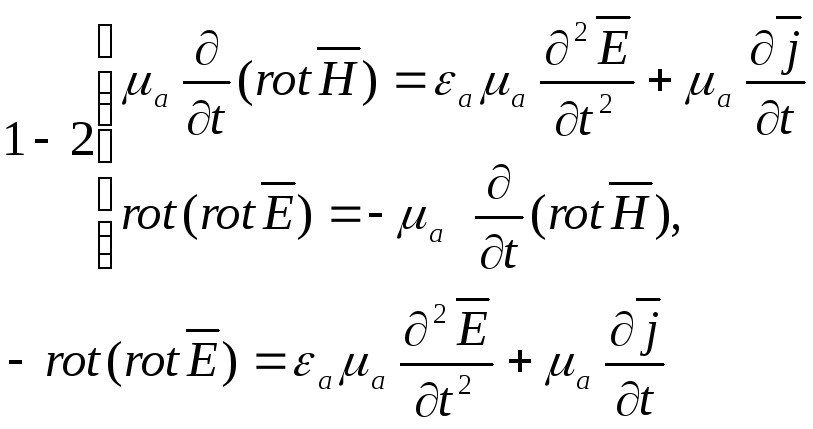
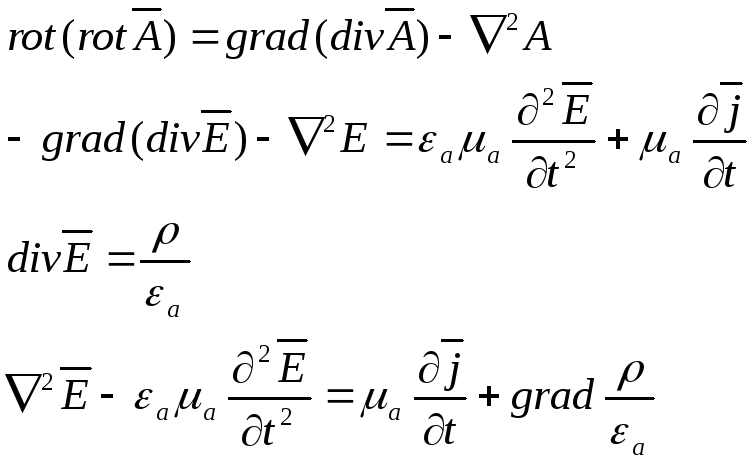
Правая часть – источник поля

II. Аналогичным образом для вектора Н

Умножим 2 на ε_а и продифференцируем:

Возьмем rot от 1

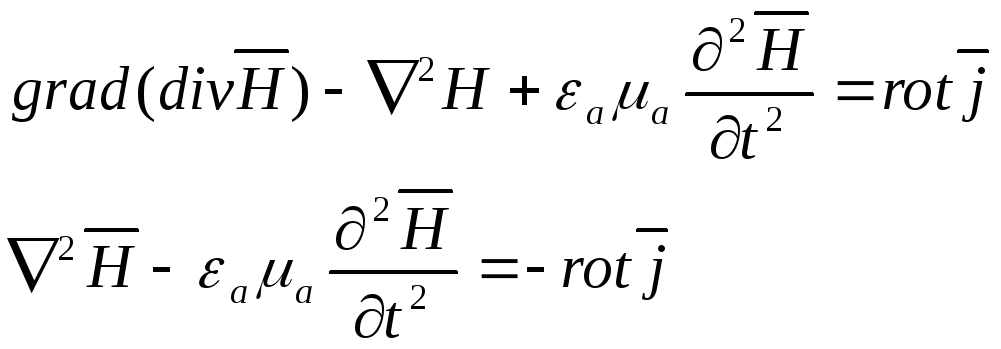
Правая часть – ток

Полученные уравнения в математической физике называется – неоднородным волновым уравнением или уравнениями типа Де Ламбера

• Если в среде не могут протекать токи

Будет только сторонний ток и:

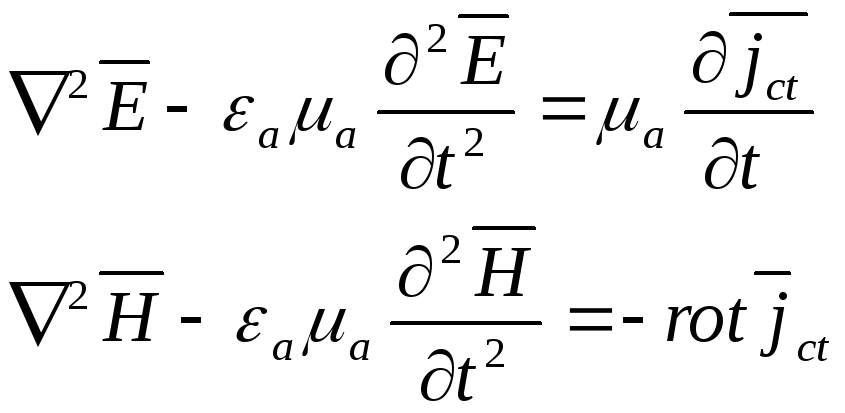
Эти уравнения векторные, поэтому каждое из уравнений могут быть записаны в виде трех скалярных для каждой проекции.

• Если отсутствуют сторонние токи

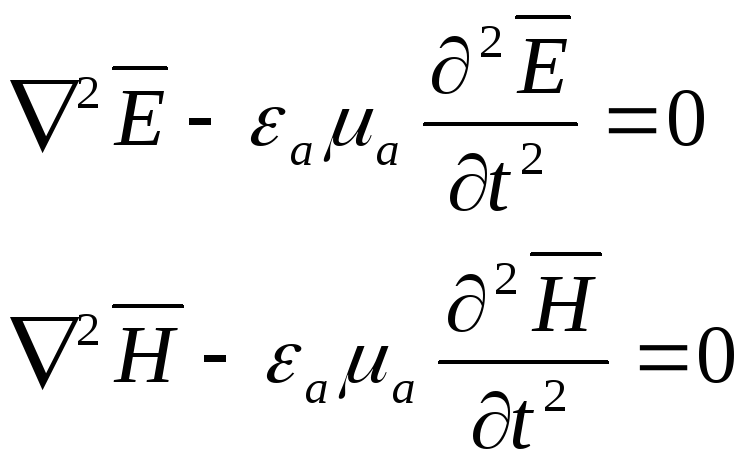
Уравнения превращаются в однородные волновые уравнения

• Если поля меняются по гармоническому закону (sin, cos), то

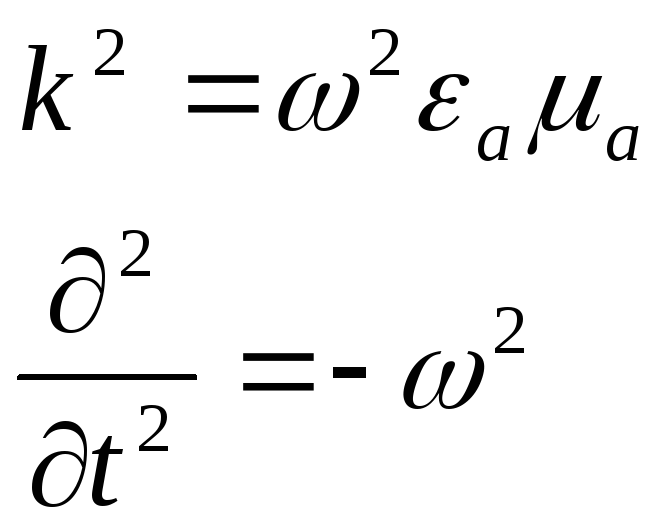
• Если поля совершенны, не зависят от времени, статические поля

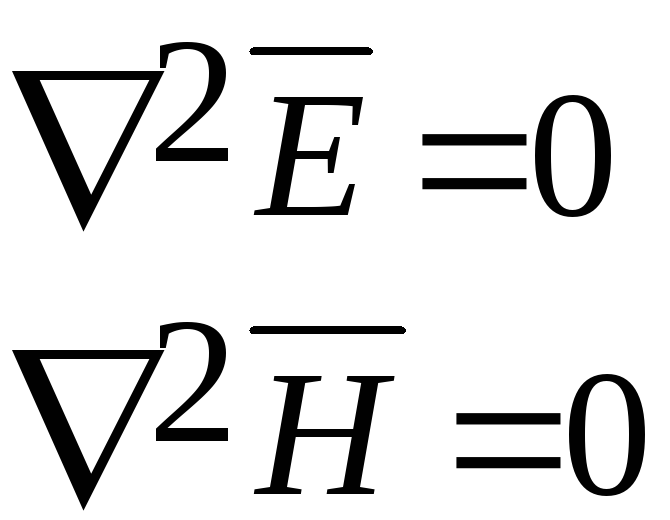
Это уравнения Лапласа в математической физике (фундаментальные уравнения)

Решения этих уравнений достаточно хорошо развиты (2 векторные уравнения или 6 скалярные уравнения)

Такие же уравнения можно получить и для вспомогательных функций (векторные потенциалы)

Билет №31.

Вопрос 1.

Граничные условия для векторов электрического поля при отсутствии на границе раздела зарядов. [= 0 ]

Иногда встречаются случаи, когда на границе

Из общих условий:

(1)

(2)

(1) : (2)

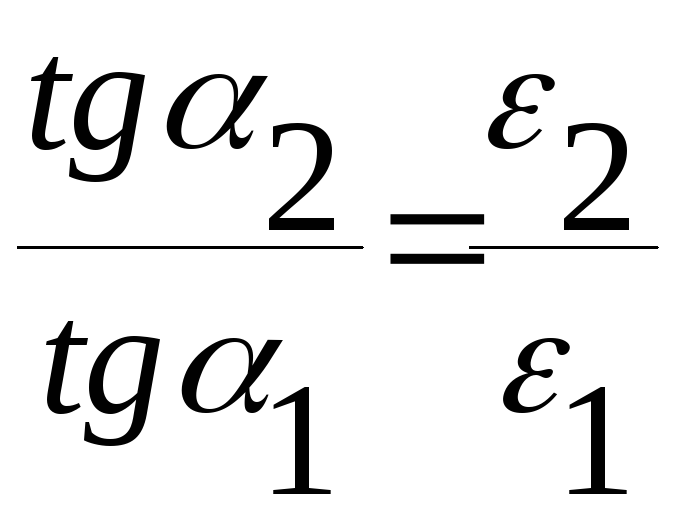
Это соотношение показывает, что при переходе из одной среды в другую, силовые линии электрического поля преломляются.

Если вектор переходит из среды с меньшей в среду с большей то во второй среде силовые линии отклоняются к границе раздела ( ) .

При этом вектор во второй среде уменьшается, а вектор – увеличивается.

(Вектор не меняется при перпендикулярном направлении перехода)

Если поле переходит из среды с большей в меньшую, то всё будет наоборот.

Вопрос 2. Плоская однородная волна в среде с потерями.

Тогда

- уравнение плоской затухающей волны

- амплитудный множитель (амплитуда убывает по экспоненциальному закону вследствие потерь)

фазовый множитель

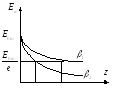
Для того, чтобы изучить скорость убывания амплитуды, вводят понятие глубины проникновения поля (а)-расстояние, по прохождении которого, амплитуда волны убывает в е раз.

, ,

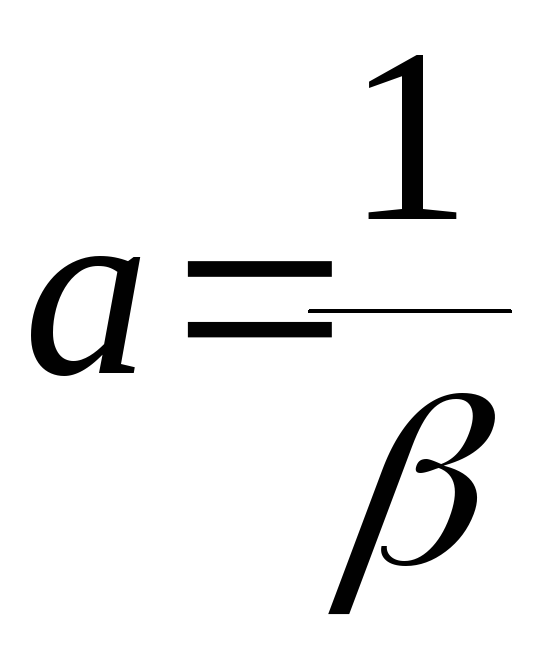
Плоская однородная волна в среде с электрическими потерями.

На практике чаще всего приходиться встречаться со средами, где есть электрические потери, а магнитные потери малы ( диэлектрики + металлы (кроме ферромагнетиков)).

Для таких сред

Коэфицент распространения

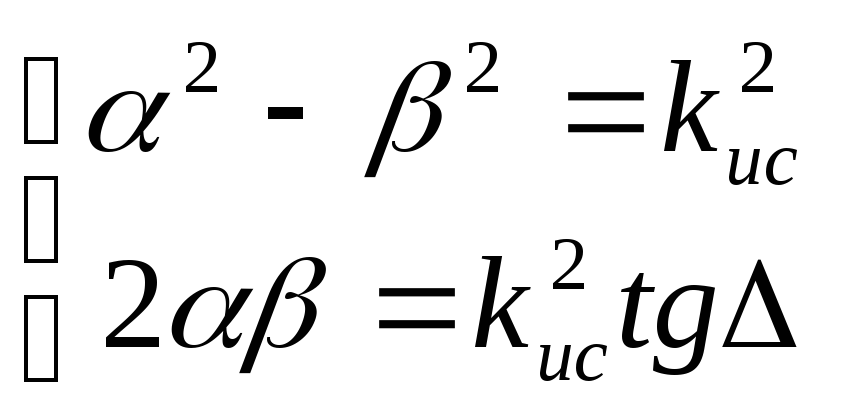
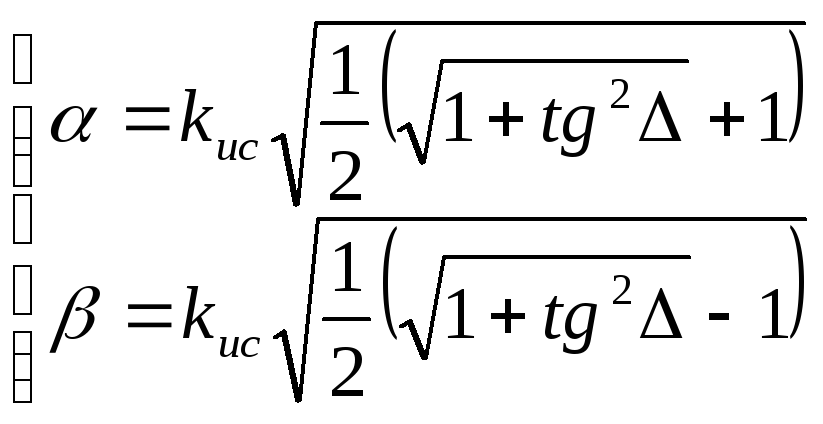
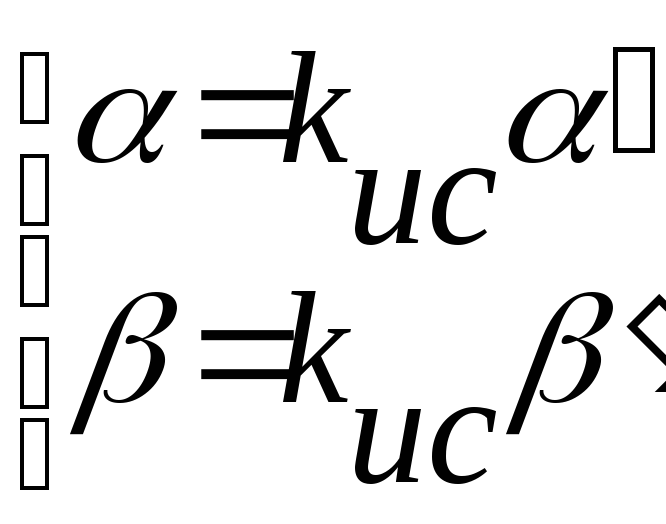
Волновое сопротивление

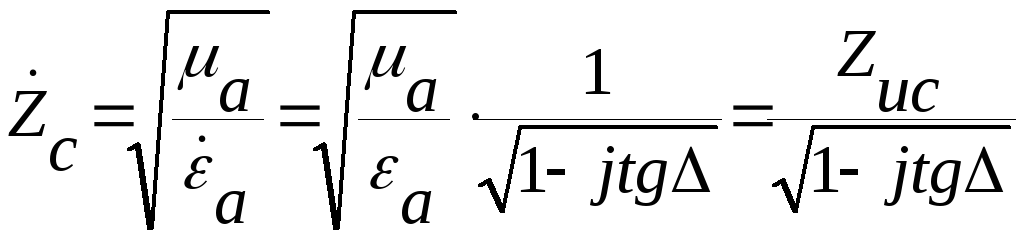
Модуль:

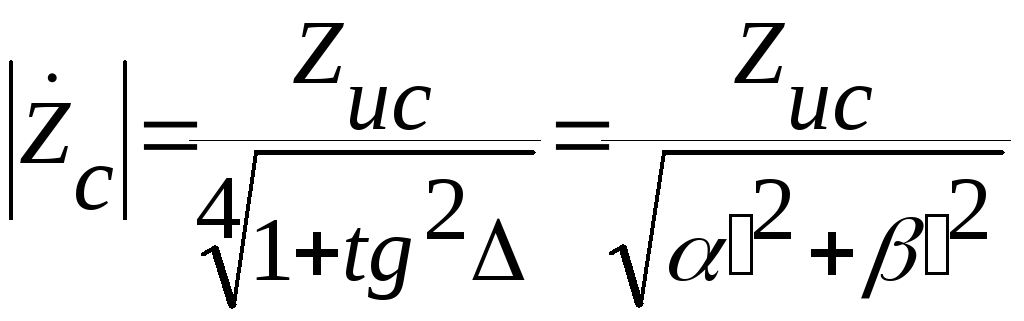
Сдвиг по фазе:

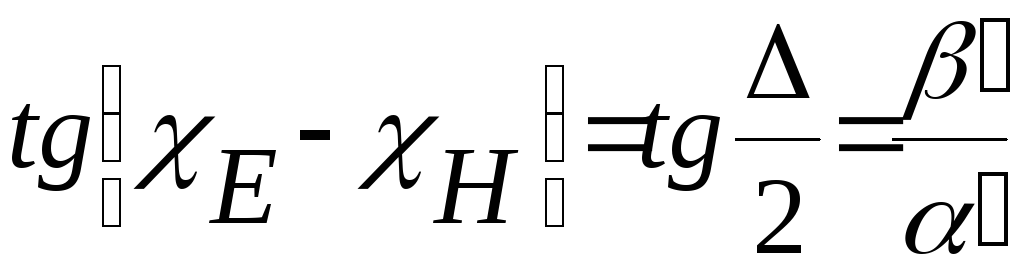
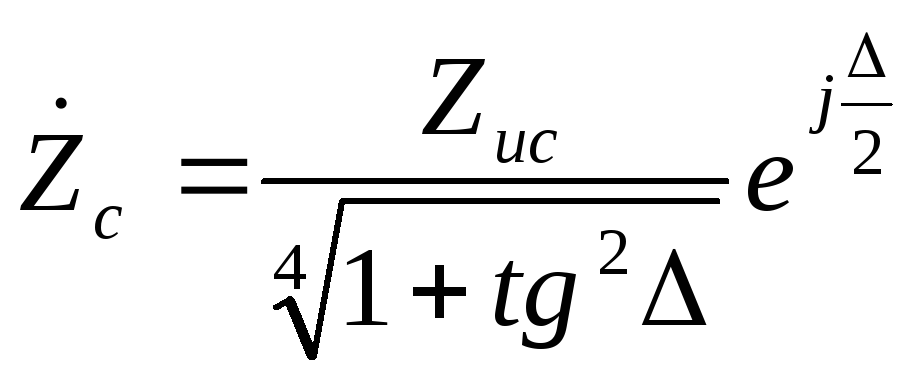
Фазовая скорость

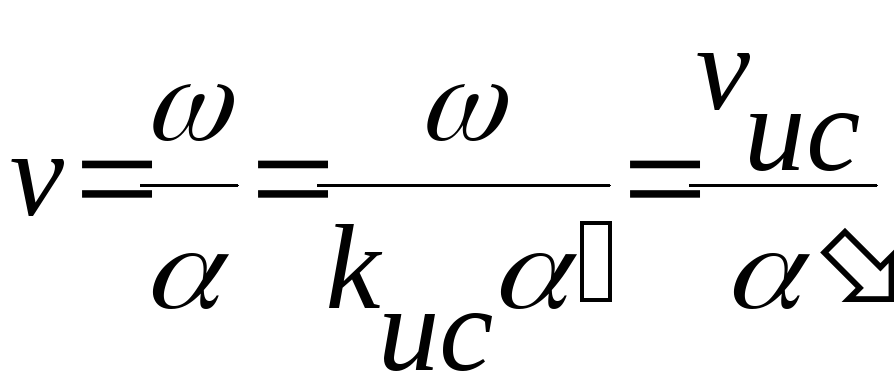
Длина волны

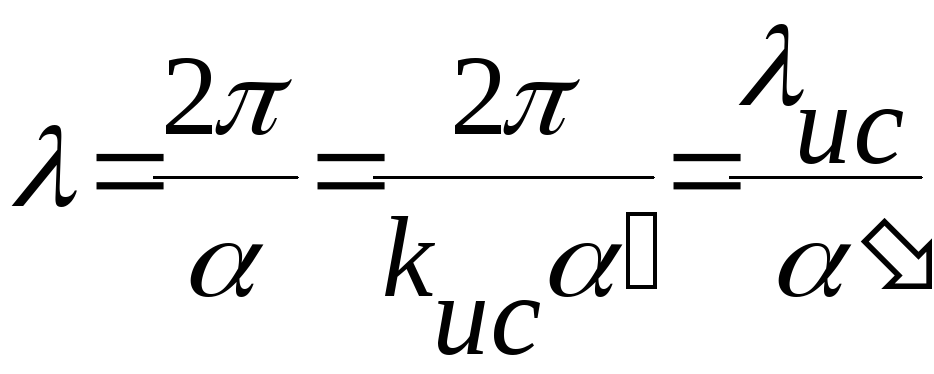
Глубина проникновения

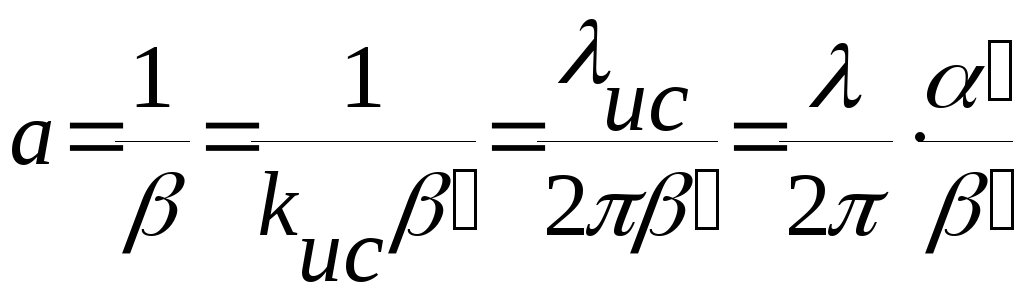
Билет №32