
- •Типы эл м волн и полей
- •2.Понятие о критическом угле паления при отражении радиоволн
- •Свойства волн типа т
- •2.Понятие о полюсно и линейно поляризованной волне
- •Свойства волн е и н типа
- •2.Понятие о круговой поляризации эл. М волн
- •Характерные особенности поверхностных электромагнитных волн
- •2. Критическая длинна волны в волноводах
- •Общие свойства поверхностных волн е и н типа
- •2.Решение волнового уравнения для поля магнитных волн в круговом волноводе
- •Билет №6
- •1 Вопрос Выбор размеров прямоугольного волновода для основного типа волны.
- •2 Вопрос Резонансная длина волны круглых резонаторов. Резонансная частота объемного резонатора.
- •Билет №7
- •1 Вопрос Диаграмма направленности элементарного электрического вибратора.
- •2 Вопрос Графическая зависимость коэффицентов Фрэнеля от угла падения плоской волны.
- •Билет №8
- •1 Вопрос Электрические волны в круглом волноводе.
- •2 Вопрос
- •Отражение плоских волн на границе идеальных диэлектриков.
- •Билет №9
- •1 Вопрос Краевая (граничная) задача для волноводов.
- •2 Вопрос Резонансная длина волны прямоугольног резонатора. Резонансная частота объемного резонатора.
- •Билет №10
- •1 Вопрос Переход от волноводов к объёмным резонаторам.
- •2 Вопрос
- •Билет 12 Закон Брюстера
- •2.Решение краевой (граничной) задачи в прямоугольном волноводе.
- •2. Режим работы волновода.
- •Распространение эл м волн в анизотропных средах.
- •2.Распространение плоской однородной волны в феррите вдоль подмагничевающего поля. Эффект Фарадея
- •Билет 17 1. Поверхностные волны над ребристой периодической металлической структурой.
- •2. Коэффициент затухания и кпд линии передач.
- •Уравнение связи
- •Билет №21.
- •1 Вопрос:”Понятие поля. Физическое поле. Виды полей”.
- •2 Вопрос:”Связь векторов поля с электрическими потенциалами”.
- •Билет №22
- •1 Вопрос:”Электрические заряды. Распределение зарядов. Плотность зарядов”.
- •Линейная плотность заряда[кул/м].
- •Принцип суперпозиции.
- •2 Вопрос: ”Интегральные теоремы Остроградского-Гаусса и Остроградского-Стокса”.
- •Билет №23
- •1 Вопрос:”Электрические токи. Сила тока и плотность тока”.
- •Объёмное распределение токов.
- •Поверхностное распределение токов.
- •Линейная плотность тока.
- •2 Вопрос:”Вектор Умова-Пойтинга. Среднее его значение за период”.
- •Билет №24.
- •1 Вопрос:”Полная система уравнений электродинамики”.
- •2 Вопрос:”Понятие о плоской однородной волне”
- •Теорема Умова-Пойтинга
- •Переход из интегральной формы к дифференциальной.
- •1.Закон электромагнитной индукции.
- •Вопрос 1. Третье уравнение электродинамики. Теорема о потоке вектора магнитной индукции.
- •Вопрос 2.
- •Вопрос 1. Четвёртое уравнение электродинамики. Теорема о потоке вектора электрическойой индукции.
- •Вопрос 2.
- •Вопрос 1.
- •Вопрос 2. Плоская однородная волна в среде с потерями.
- •Вопрос 1.
- •Вопрос 2. Плоская однородная волна в среде с потерями.
- •Вопрос 1.
- •Сопротивление проводников при поверхностном эффекте.
- •Вопрос 2.
2. Коэффициент затухания и кпд линии передач.
При распространении по линии передач
напряженность электрического поля
меняется по закону:![]() ,
,
![]() -направление
в начале линии.
-направление
в начале линии.
Так как передаваемая мощность
пропорциональна квадрату напряженности
электрического поля, то
![]() ,
,
![]() -мощность
в начале линии.
-мощность
в начале линии.
![]()
Коэфицент затухания: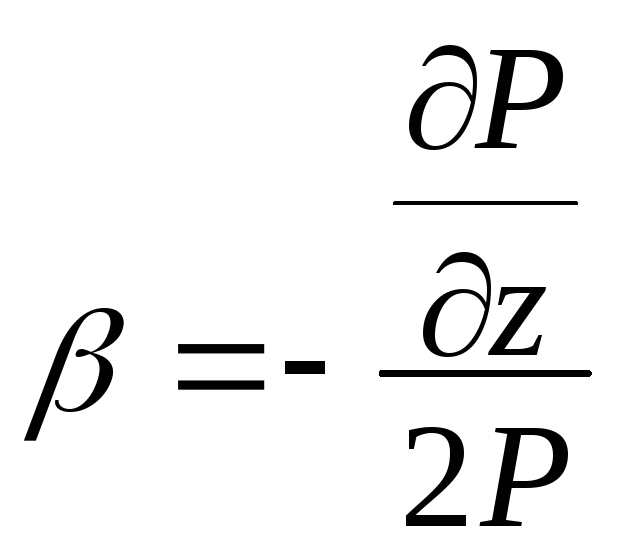 ,
,
![]() - скорость затухания мощности по оси Z
- скорость затухания мощности по оси Z
Найдем коэфицент затухания для
прямоугольного волновода с волной
![]() .
.
Потери:
![]() ,
,
![]() -удельное
поверхностное сопротивление
-удельное
поверхностное сопротивление
Плотность потерь:![]()
На бесконечно малом отрезке длиной
![]() элементарные потери:
элементарные потери:
![]()

![]()
![]()
![]()

![]()
![]()
![]()
Плотность тока можно найти с помощью касательной составляющей магнитного поля.
Таким образом, формула для расчета
коэффициента затухания в прямоугольном
волноводе с волной
![]() :
:
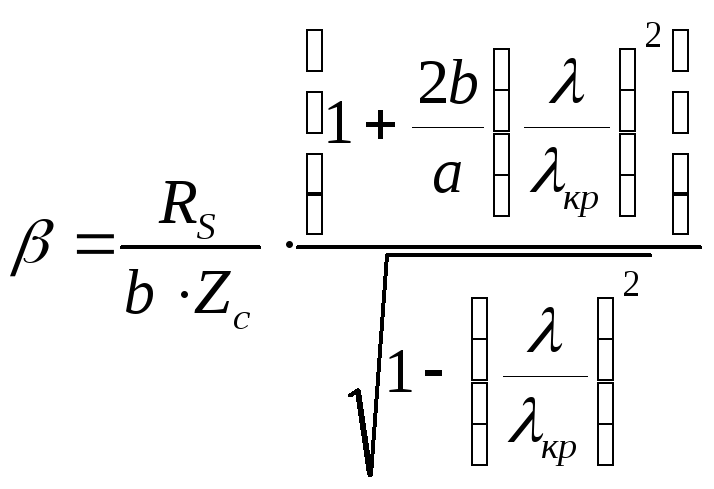
![]()
Билет 18 1. Замедленные электромагнитные волны и замедляющие структуры.
Замедленными электромагнитными волнами называют волны, фазовая скорость которых меньше скорости света в пустоте.
Несмотря на то, что изученные нами плоские однородные волны имеют во всякой среде, отличной от вакуума, принципиально замедленную скорость, понятие замедленная относиться только к направленным волнам , к волнам, распространяющимся вдоль структуры.
Также это определение относиться и к волнам, отличных от типа Т (к ПОВ).
Такие направленные структуры, поддерживающие замедленные волны, называются замедленными структурами.
Помимо замедленной фазовой скорости таких волн характерной их особенностью является экспоненциальное спадание амплитуд поля в направлении распространения, и наличие продольной составляющей вектора Е или Н (или обоих сразу), следовательно, замедленные волны являются неоднородными электромагнитными волнами.
Электромагнитное поле и основная часть энергии, переносимой волной, локализована вблизи направления структуры, и поэтому замедляющую волну часто называют поверхностной волной.
Её поверхностный характер и замедление фазовой скорости неразрывно связаны, в связи с чем понятие «замедленная» и «поверхностная» физически являются одинаковыми.
Замедленные электромагнитные волны находят широкое применение в ряде устройств, например, в линии передачи, а также для устройства излучающих элементов с поверхностной волной, в усилителях и генераторов СВЧ типа ЛБВ и ЛОВ, в ускорительных элементах заряженных частиц.
Возникновение замедленных или поверхностных волн вдоль направления структуры требует наличие определенного поверхностного импеданса этой структуры, то есть наличия продольной составляющей вектора Е или Н.
Следовательно, поверхностные волны могут распространяться по таким структурам в форме Е- или Н- волн.
При этом конструкция исполнения направляющей структуры не имеет принципиального значения, она может быть гладкой, периодической, носить сложный характер.
2.Критческий угол падения(угол полного внутреннего отражения)
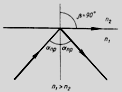
Если свет падает из оптически более плотной среды в оптически менее плотную, то при определенном для каждой среды угле падения, преломленный луч исчезает. Наблюдается только преломление. Это явление называется полным внутренним отражением.
Угол падения, которому
соответствует угол преломления 90°,
называют предельным
углом полного внутреннего отражения
(0).
Из закона преломления следует, что при
переходе света из какой-либо среды в
вакуум (или воздух) ![]()
№19
-
Распространение плоской волны в феррите поперек подмагничивающего поля
Особенности распространения электромагнитных волн в конкретной
среде определяются свойствами этой среды. В электродинамике для локального описания свойств среды используют материальные уравнения:
![]()
Коэффициенты (εа), (μа) и (σ) в общем случае являются тензорами и могут зависеть от ряда параметров. Характер этих зависимостей положен в основу классификации различных сред. Так, если свойства среды зависят от направления приложенных полей Е и Н, то такие среды называют анизотропными.
В анизотропных средах направление приложенного поля не совпадает с направлением
вызванного этим полем отклика.
Частным случаем анизотропных сред являются гиротропные среды, для которых хотя бы один из тензоров (ε), (μ) имеет вид:
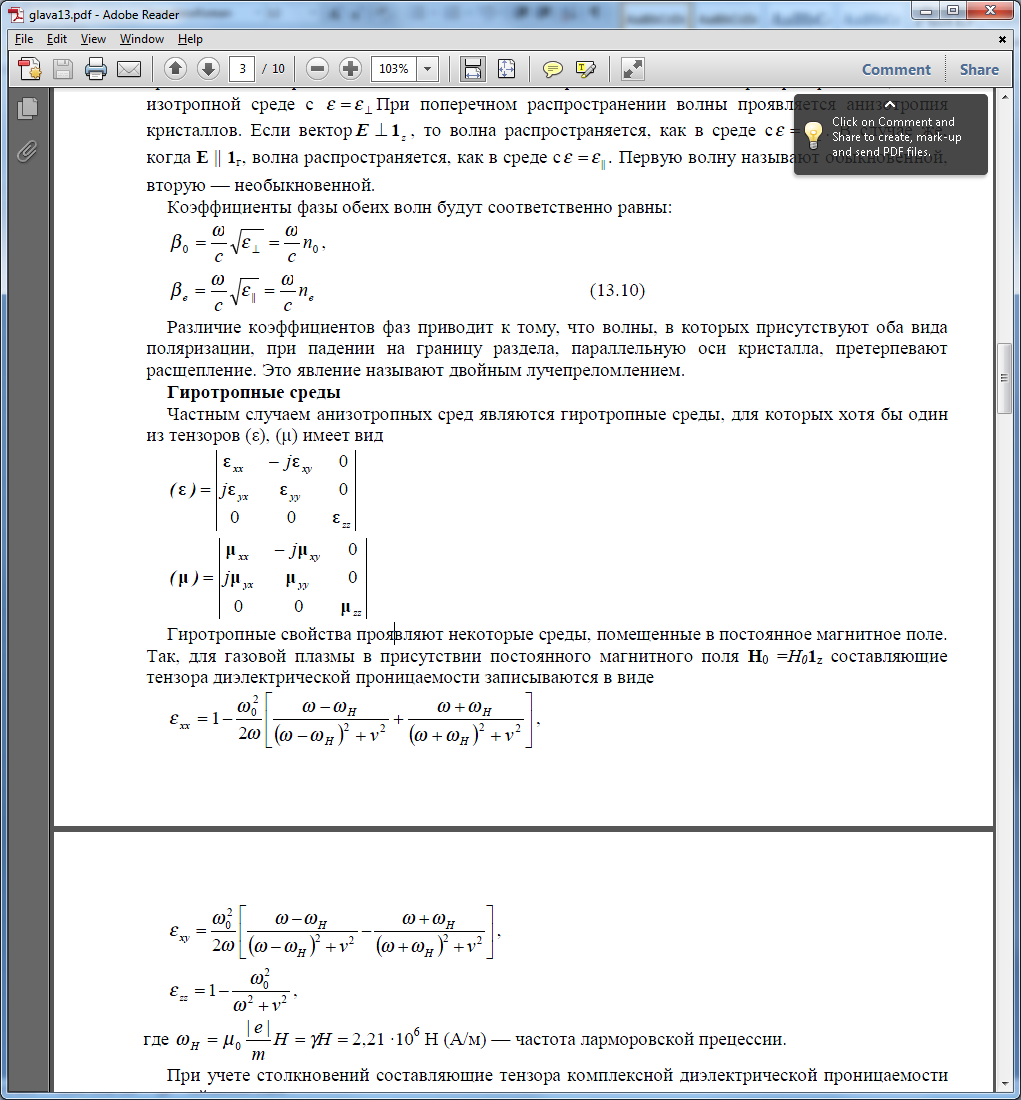
Гиротропные свойства проявляют некоторые среды, помещенные в постоянное магнитное поле. Так, для газовой плазмы в присутствии постоянного магнитного поля Н0 =H01z составляющие тензора диэлектрической проницаемости записываются в виде
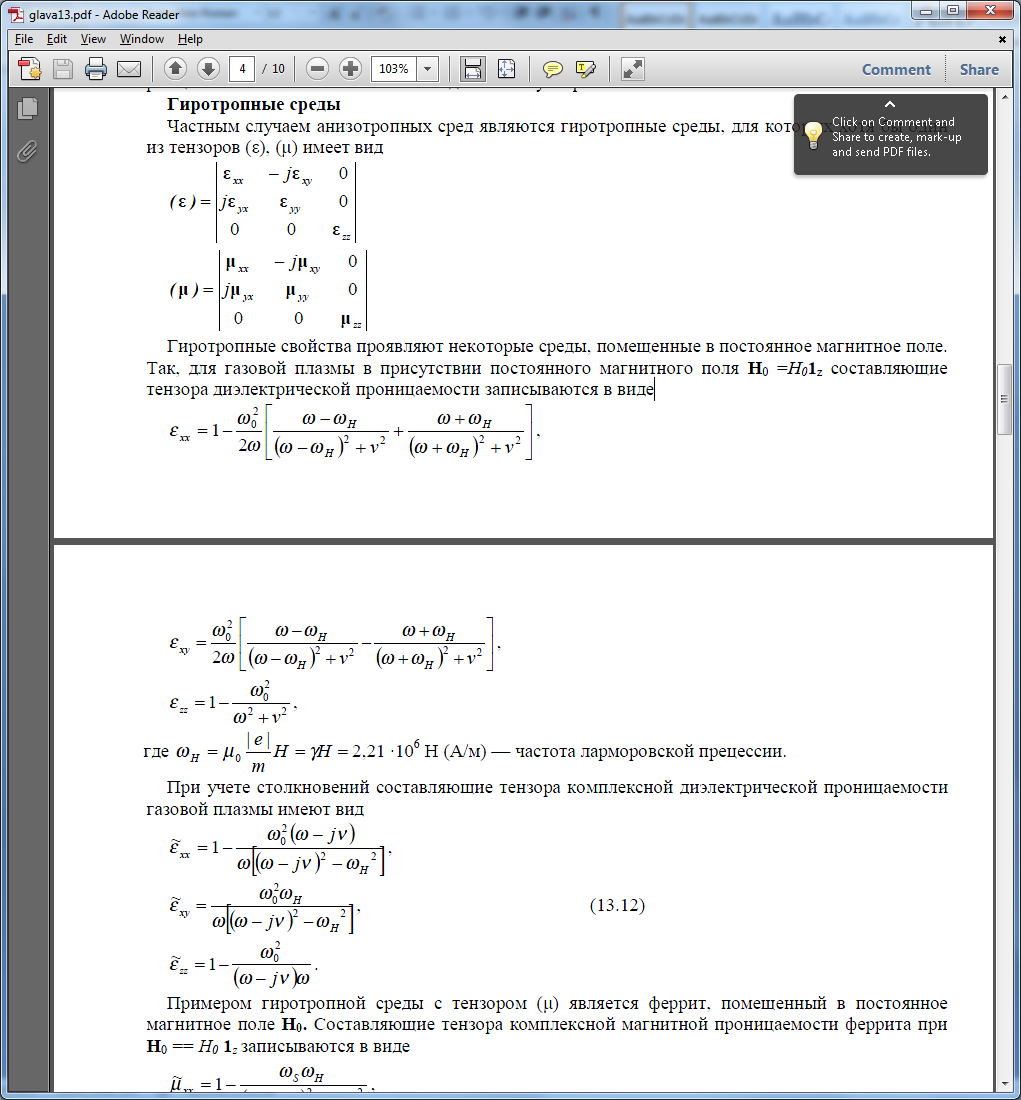
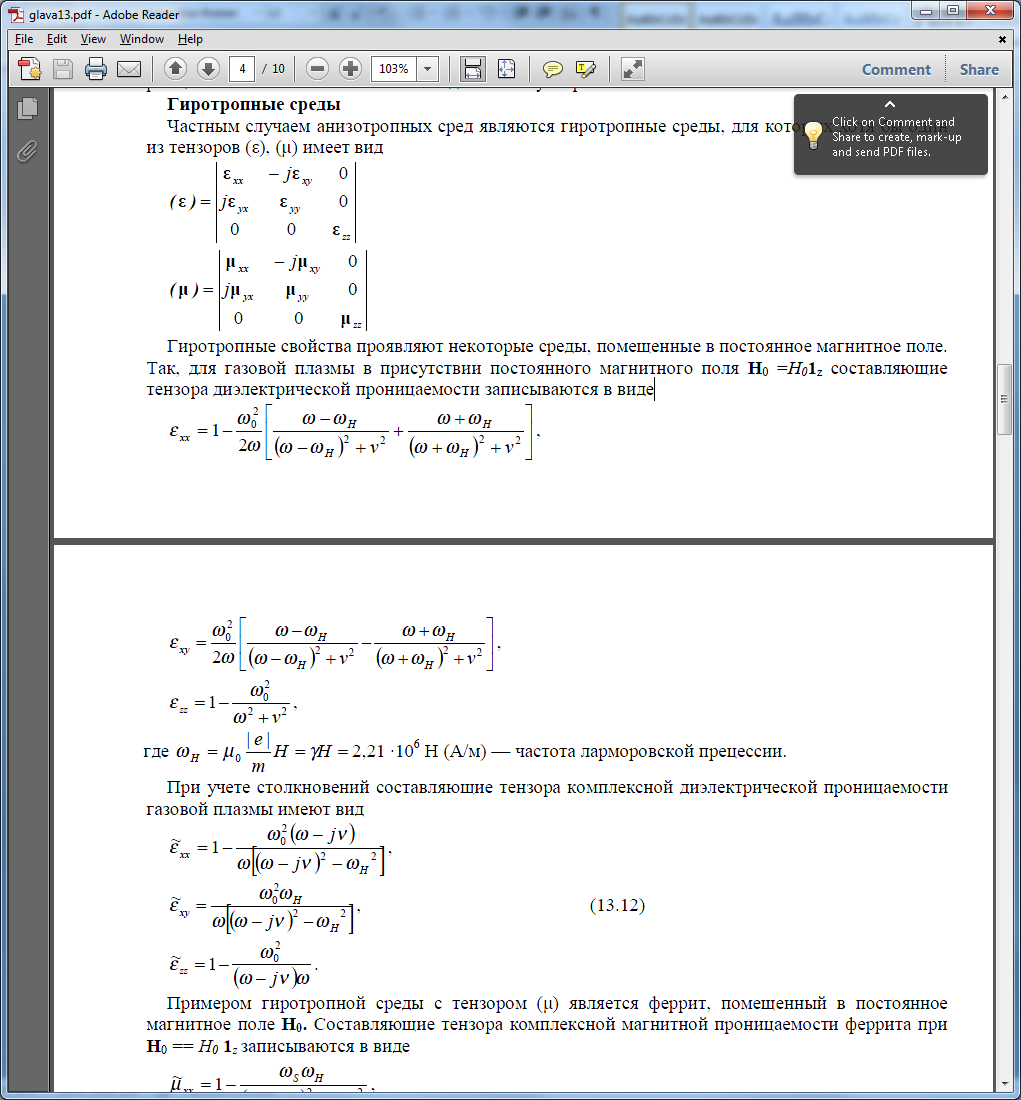
При учете столкновений составляющие тензора комплексной диэлектрической проницаемости газовой плазмы имеют вид:
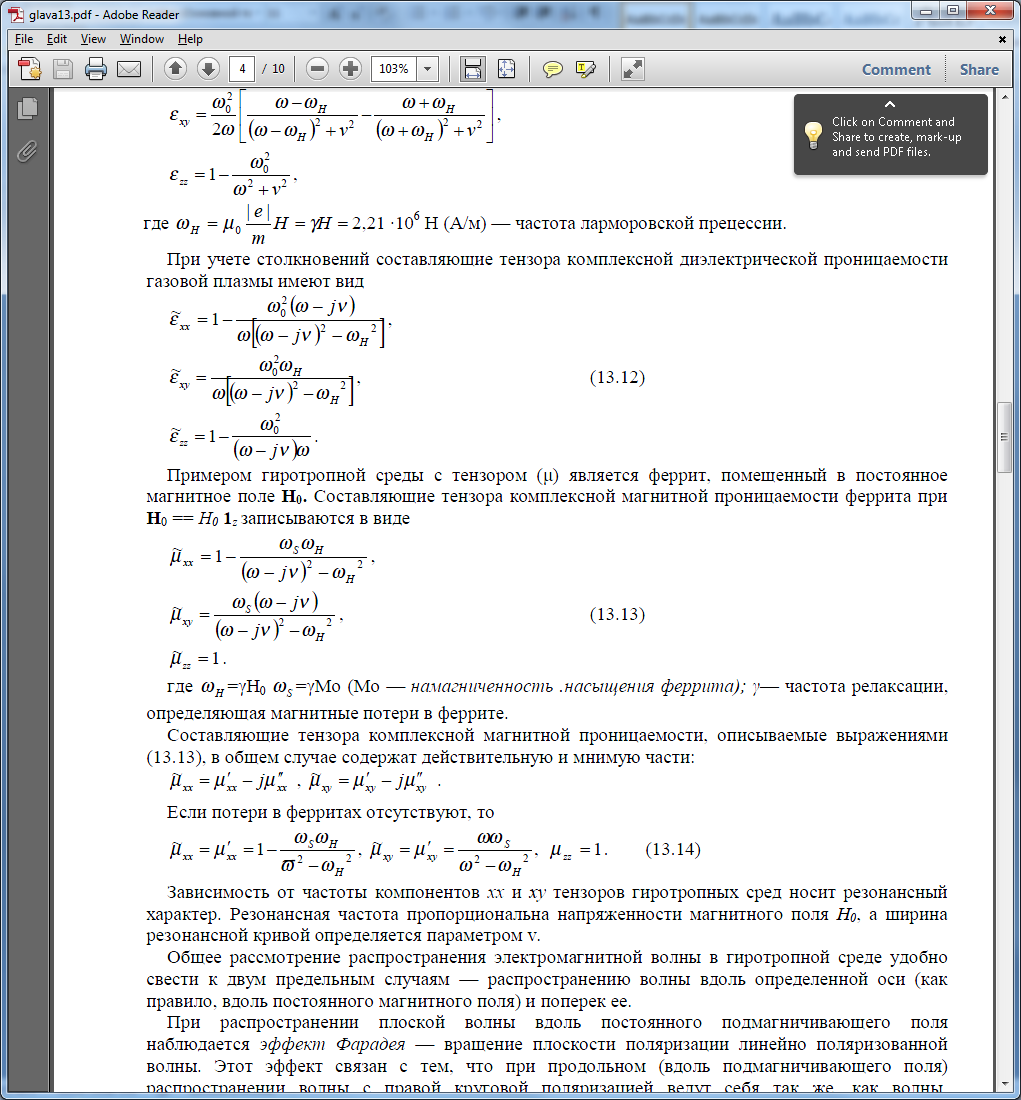
Примером гиротропной среды с тензором (μ) является феррит, помещенный в постоянное
магнитное поле Н0. Составляющие тензора комплексной магнитной проницаемости феррита при Н0 == Н0 1z записываются в виде:
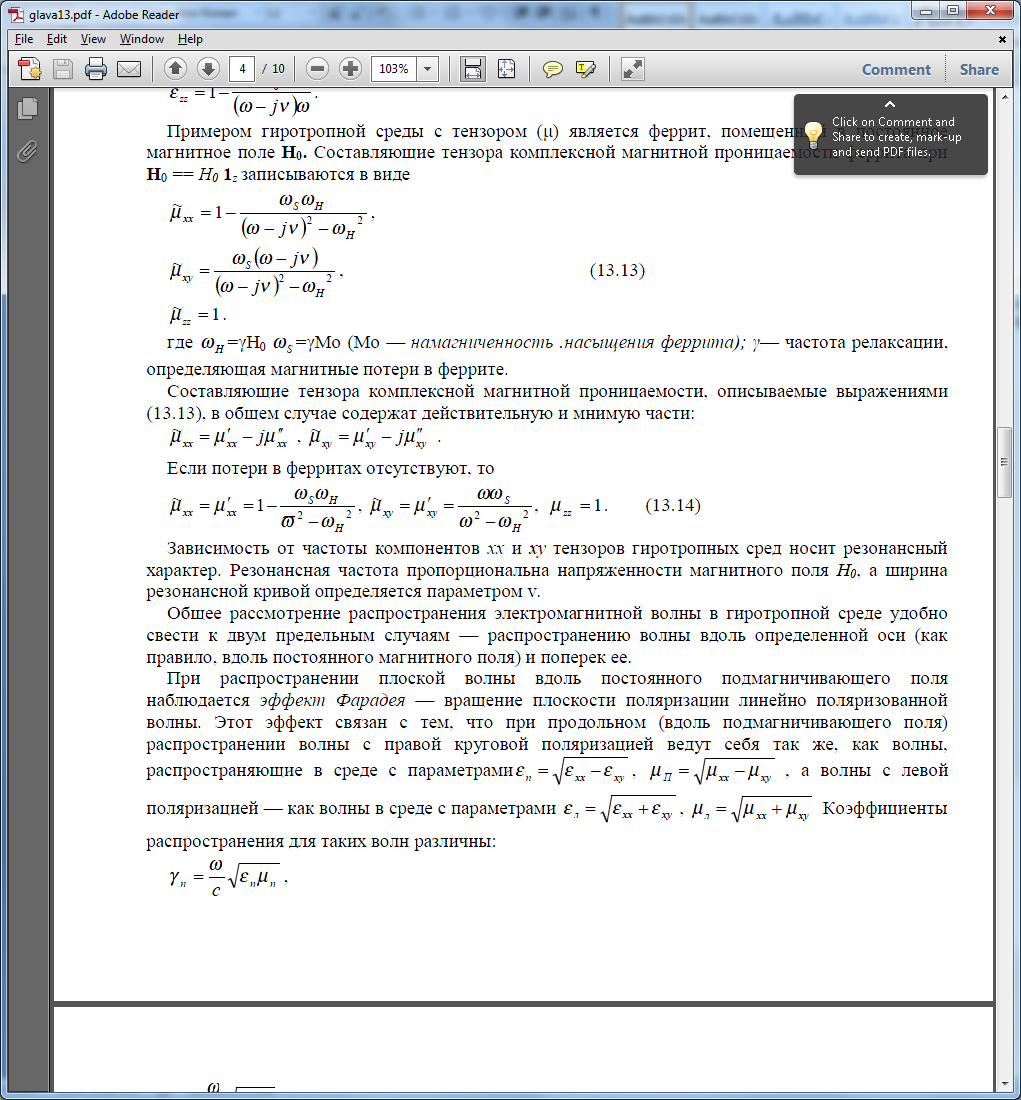
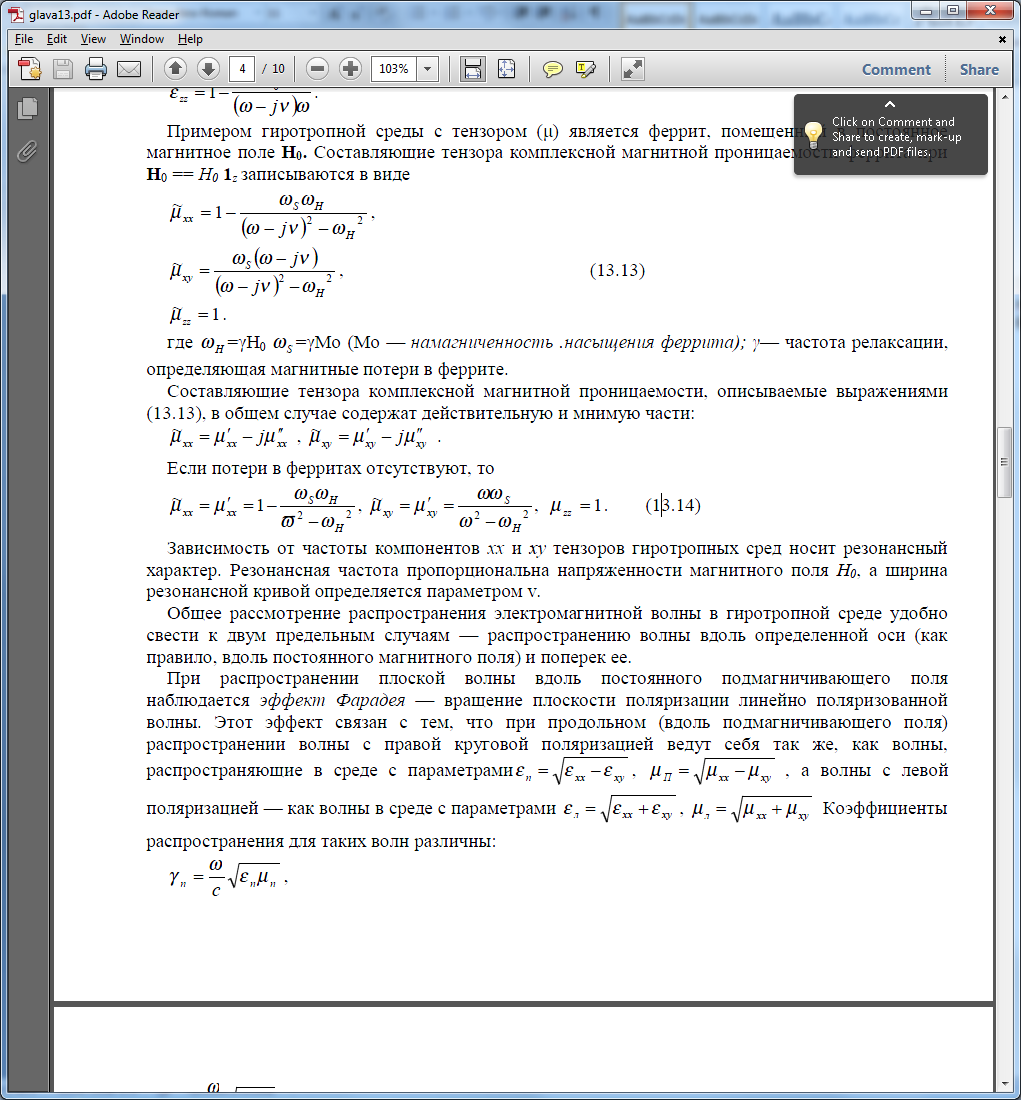
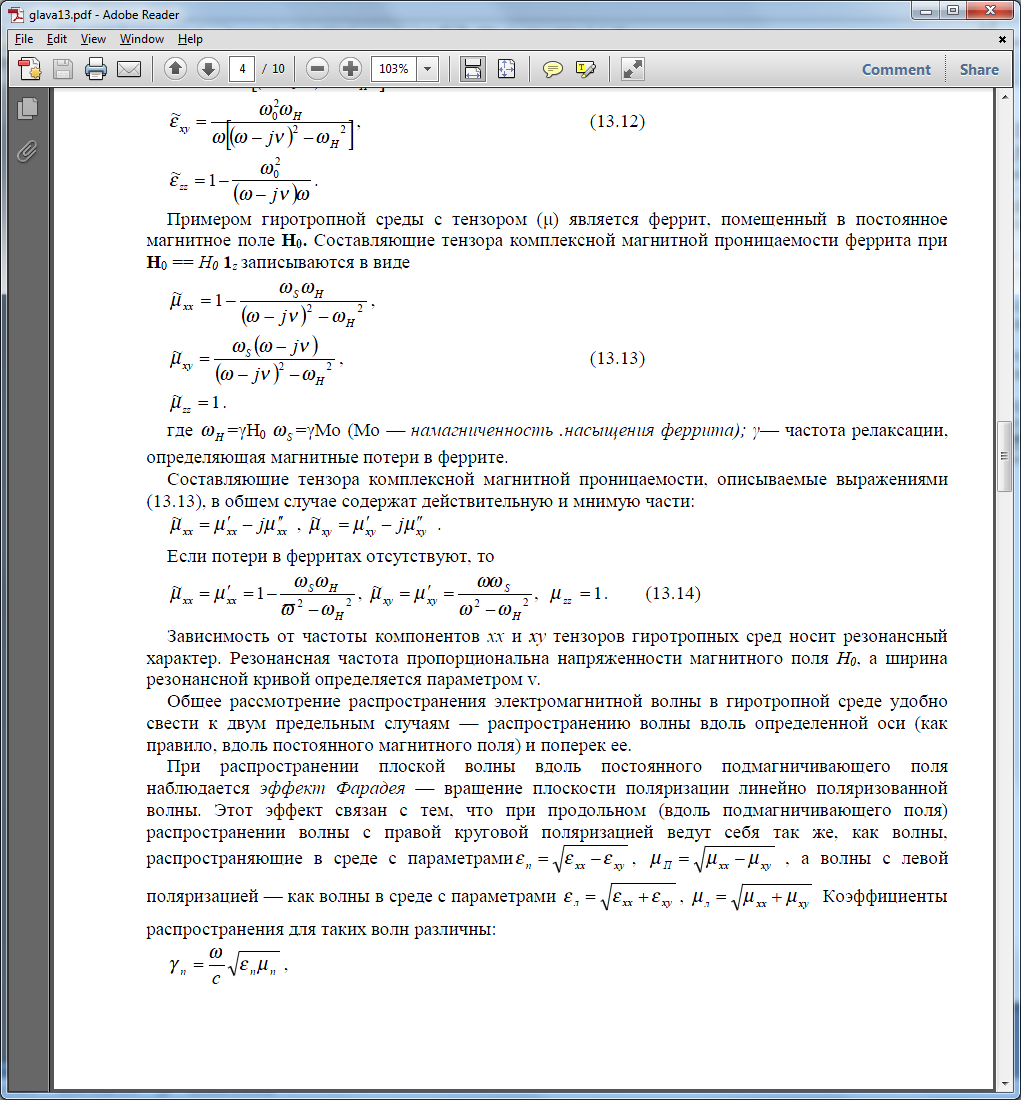
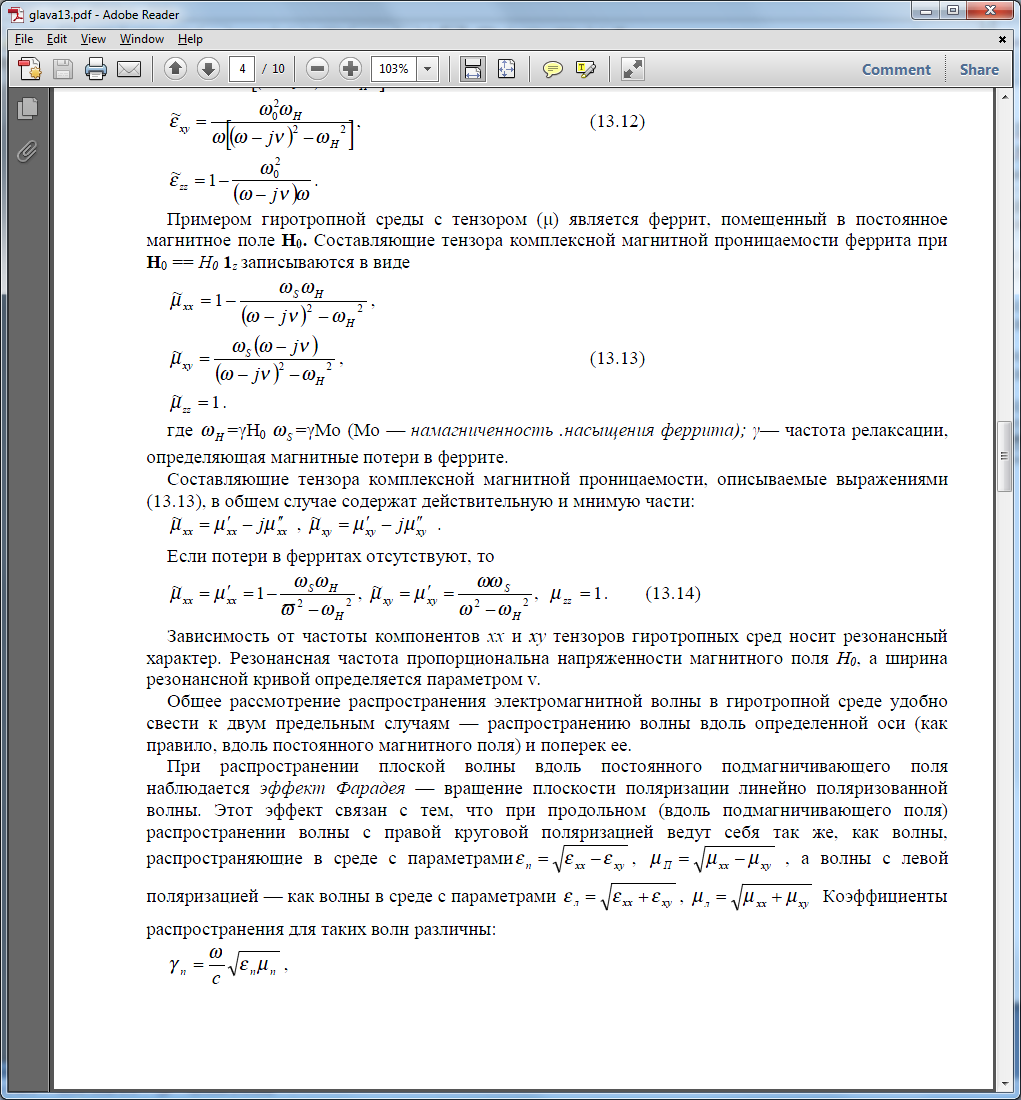

-
Графическая зависимость коэффициентов Френеля от угла падения плоской волны
Отражение и преломление плоской э/м волны при ее падении на плоскую границу 2х сред определяется коэффициентами Френеля. Коэффициент отражения для горизонтально поляризованной волны (она называется волной с перпендикулярной поляризацией). R(инд.г)(а сверху еще точка)==E1(с точкой сверху)/ E0(сверху точка)=(cosθ1 – √(ε2/ε1)-sin(c.2)θ1`)/
/(cosθ1+√(ε2/ε1)-sin(c.2)θ1`)= (cosθ1 - √ε-sin(c.2)θ1`)/ (cosθ1+√ε-sin(c.2)θ1`).
θ1 – угол между направлениями падающего луча и нормалью к поверхности. ε1,ε2 – относительные диэлектрические проницаемости, в воздухе ε=1. Для вертикально поляризованной волны она называется волной с параллельной поляризацией, вектор Е0 когда лежит в плоскости падения, коэффициент отражения
R(инд.в)(сверху точка)=E1(с точкой)/E0(с точкой)= - (ε2 cosθ1 - √ε1` √ε2 – ε1 *sin(c.2)θ1`)/(ε2 cosθ1 + √ε1` *√ε2 – ε1 sin(c.2)θ1`).
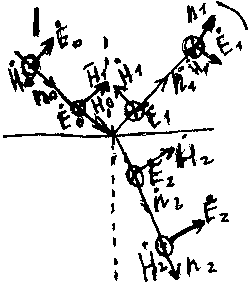
При нормальном падении коэффициенты R(инд.г) и R(инд.в) совпадают и равны (1-√2`)/(1+√2). Иногда коэффициент отражения определяется как отношение вектора напряженностей магнитного поля. Коэффициент Френеля величина комплексная, характеризуется амплитудой и фазой. R(инд.в,г)(сверху точка) = =R(инд.в,г) e(c.-jφ(инд.в,г)).
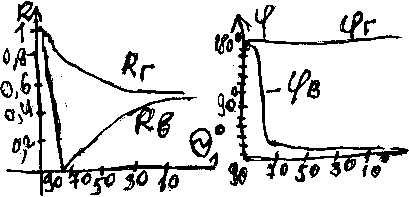
Зависимость Rв, Rг от угла падения θ показана на рисунке, как видно для горизонтальной
поляризации можно принять, что φ(инд.г)=180°, а Rг= -1. Для реальных сред Rв достигает минимума вблизи угла Брюстера (θ≈73°).
На рисунке слева – зависимость модуля коэффициента Френял при горизонтальном и вертикальном падении волны на грунт. Справа фазы коэффициентов Френеля при горизотальной и вертикальной поляризации при падении э/м волны на грунт. Формула коэффициентов Френеля для волн оптического диапозона – в методичке.
№20
-
Понятие о средах и их видах
Материи (среды – вещества), в которых изучаются электромагнитные явления. Они могут быть безграничными или занимать конечную часть пространства. Будем различать однородные и неоднородные среды.
Среда называется однородной, если
параметры среды везде или в данной части
пространства не изменяются, т.е. не
зависят от координат
![]()
![]()
![]()
![]()
В противном случае среда будет неоднородной.
Вакуум является особой средой, но он материален. Он не содержит обычных корпускулярных видов материи, но он не пуст, его заполняют различные физические поля.
Будем различать анизотропные и изотропные среды.
Среда называется изотропной, если
взаимодействие поля со средой не зависит
от направления его приложения
![]() ,
,
а для анизотропной среды любая координата
![]()
Анизотропные среды характеризуются тензорными параметрами.
Будем различать линейные среды и нелинейные.
Среда называется линейной, если в ней параметры, её характеризующие не зависят от интенсивности приложенного поля. Всегда является линейной, как правило, при малых интенсивностях. Для линейной среды справедлив принцип суперпозиции.
Н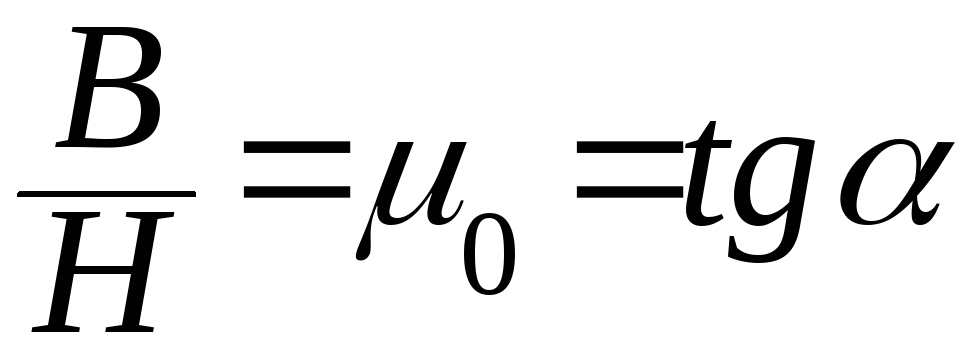 елинейность
среды проявляется при больших полях
и заключается в зависимости параметров
среды от интенсивности поля.
елинейность
среды проявляется при больших полях
и заключается в зависимости параметров
среды от интенсивности поля.
Уравнения электродинамики изучаются, главным образом, в однородных линейных изотропных средах.
-
Волноводные уравнения для электродинамических потенциалов
Запишем систему уравнений электродинамики для однородного изотропного пространства:
Из уравнения 3:
![]()
![]() вектор
вектор
![]() является вихревым полем, это означает,
что мы можем предполагать, что вектор
является вихревым полем, это означает,
что мы можем предполагать, что вектор
![]() - вихрь какого-нибудь другого вектора.
- вихрь какого-нибудь другого вектора.
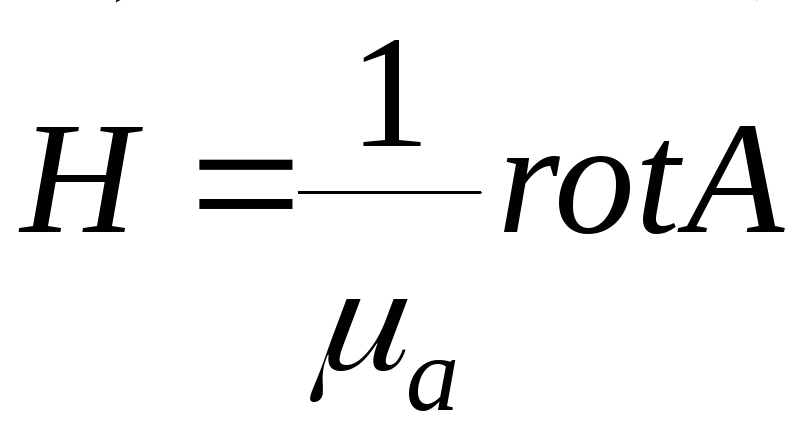 (div rot
(div rot![]() )
)
Подставим
![]() в уравнение 2:
в уравнение 2:
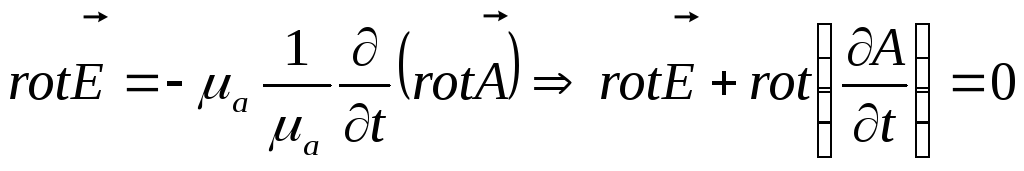
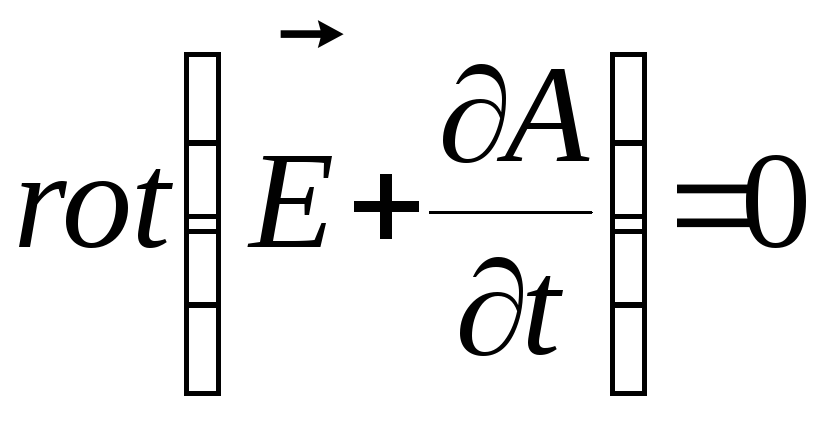
Эта запись означает, что вектор
![]() - безвихревое поле или потенциальное.
- безвихревое поле или потенциальное.
А потенциальное поле можно описать с
помощью одной единственной скалярной
функцией
![]()
![]() =
-grad
=
-grad![]() .
Отсюда видно:
.
Отсюда видно:
![]()
Таким образом, мы выразили вектора
![]() и
и
![]() через
через
![]() и
U. Подставим
и
U. Подставим
![]() и
и
![]() в 1 уравнение:
в 1 уравнение:
![]()
![]()
![]()
![]()
![]()
rot
![]()
![]()
![]() rot
rot
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
До этого, вводя величину
![]() ,
мы связали вектора
,
мы связали вектора
![]() и
и
![]() неоднозначно:
неоднозначно:
![]()
rot grad![]()
![]() ,
таким образом пусть:
,
таким образом пусть:
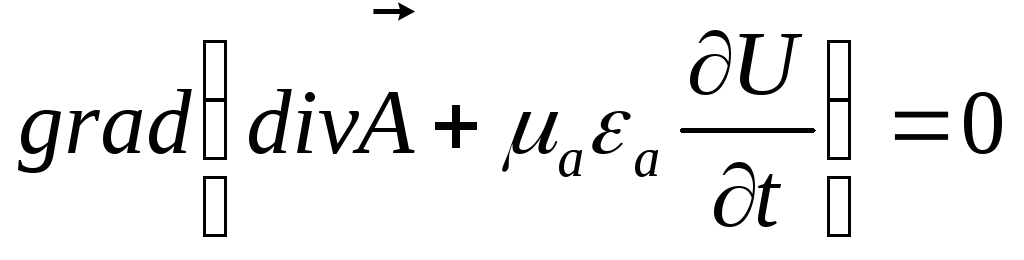
![]()
![]() =
0
=
0![]()
