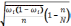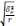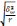6.3. Ошибка выборки

В процессе проведения выборочного наблюдения могут возни­кать ошибки двух видов: регистрации и репрезентативности. Случай­ных и систематических ошибок регистрации и систематических оши­бок репрезентативности можно избежать при правильной организации и проведении наблюдения. Случайных ошибок репрезентативности избежать невозможно, поскольку они возникают в силу того, что вы­борочная совокупность не полностью воспроизводит генеральную. Однако среднюю величину случайной ошибки можно рассчитать, пользуясь методами теории вероятностей.

Применяя выборочной метод, в статистике используют два вида обобщающих показателей: средняя величина количественного при­знака; относительная величина альтернативного признака (доля единиц совокупности, обладающих признаком).

В соответствии с двумя видами обобщающих показателей суще­ствует два вида формул средней ошибки выборки: для расчета сред­ней ошибки средней величины количественного признака в вы­борке; для расчета средней ошибки доли. Эти формулы в свою оче­редь имеют разновидности, зависящие от способа отбора.

Введем следующие обозначения:

N - объем генеральной совокупности (число составляющих ее единиц);

- объем выборки (число обследованных единиц);

- средняя величина признака в генеральной совокупности(генеральная средняя);

- средняя величина признака в выборочной совокупности (выборочная средняя);

- доля единиц, обладающих изучаемым признаком в генеральной совокупности (генеральная доля);

- доля единиц, обладающих изучаемым признаком в выбо­рочной совокупности (выборочная доля);

- генеральная дисперсия;

- выборочная дисперсия (для больших выборок, т. е. при );

- число серий в генеральной совокупности; г - число отобранных серий.

В табл. 6.1 приведены основные формулы для расчета ошибки выборки.

Таблица 6.1

Формулы для расчета ошибки выборки при различных способах формирования выборочной совокупности

Вид выборки	Для средней величины количественного признака ()			Для доли альтернативного признака ()
	Повторный отбор	Бесповторный отбор	Повторный отбор		Бесповторный отбор
Собственно-случайная, механическая
Типическая (при отборе, пропорциональном объему группы)
Серийная

Сопоставление формул повторного и бесповторного отбора свидетельствует о том, что применение последнего приводит к уменьшению ошибки выборки. В тех случаях, когда численности генеральной совокупности (N) очень велика по сравнению с числом отобранных единиц (n), ошибку бесповторного отбора можно определить по формуле для повторного отбора (lim (1-n) / N → 1).

Исходя из приведенных выше формул можно утверждать, что средняя величина случайной ошибки репрезентативности зависит от принятого способа формирования выборочной совокупности, объема выборки, степени колеблемости изучаемого признака в генеральной совокупности.

Для решения практических задач выборочного обследования расчета средней ошибки выборки недостаточно. Так, из генеральной совокупности может быть получено несколько выборок. При этом фактическая ошибка каждой конкретной выборки может быть больше или меньше средней ошибки. Поэтому помимо средней, рассчитыва­ется предельная ошибка выборки. Ее величина зависит от того, с какой вероятностью должна гарантироваться ошибка выборки. Уро­вень доверительной вероятности определяется при помощи специаль­ного коэффициента t, называемого коэффициентом доверия. Наибо­лее часто употребляются следующие уровни доверительной вероятно­сти и значений t:

t=1P=0,683; t=2P=0,954; t=3P=0,997

Расчет предельной ошибки производится по формулам (6,1) и (6,2):

Величина генеральной средней или доли представляется в виде пределов следующим образом (6,3) и (6,4):

Таким образом, по результатам выборочного наблюдения с оп­ределенной степенью достоверности можно утверждать, что гене­ральная средняя или доля не выйдет за установленные пределы.

Пример. Из партии лампочек в 1000 шт. отобрано способом случайной бесповторной выборки 100 шт. Средняя продолжитель­ность горения по отобранной части составляет 1200 ч, а среднее квадратичное отклонение 200 ч. Из отобранных лампочек 90 шт. удовлетворяли стандарту. Требуется определить границы среднего значения продолжительности горения (с вероятностью 0,997), а также границы доли лампочек, удовлетворяющих стандарту (с веро­ятностью 0,954), во всей партии.

Средняя ошибка средней продолжительности горения лампочек оп­ределяется по формуле собственно-случайного бесповторного отбора:

Предельная ошибка средней продолжительности горения лампочек определяется с учетом коэффициента доверия, соответствующего требуемому уровню доверительной вероятности (t = 3 при P = 0,997):

Пределы средней продолжительности горения лампочек в партии:

Таким образам, с вероятностью Р=0.997 можно утверждать, что средняя продолжительность горения лампочек во всей партии будет заключена в пределах от 1143 до 125Т ч.

Доля лампочек в выборке, удовлетворяющих стандарту (выборочная доля), составляет

Средняя ошибка доли стандартных лампочек определяется по формуле для собственно-случайного бесповторного отбора:

Предельная ошибка доли стандартных лампочек определяется с учетом коэффициента доверия, соответствующего требуемому уровню доверительной вероятности (t = 2 при P = 0,954):

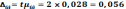
Пределы доли лампочек, удовлетворяющих стандарту, во всей партии

С вероятностью Р-0,954 можно утверждать, что доля лампочек, удовлетворяющих стандарту, во всей партии будет заключена в пределах от 84,4 до 95,6%.

Пример. 10%-ный бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проводимый с целью оценки потерь рабочего времени из- за временной нетрудоспособности, привел к результатам, представленным в таблице. Из числа обследованных 90 рабочих первого цеха, 120 рабочих второго цеха и 70 рабочих третьего не имели случаев нетрудоспособности. С вероятностью 0,954 требуется определить границы среднего числа дней нетрудоспособности, а также границы доли рабочих, не имевших случаев нетрудоспособности, по предприятию в целом.

Цех	Всего рабочих, чел.	Обследовано, чел.	Число дней временной нетрудоспособности за год
			средняя	дисперсия
1	1000	18	18	49
2	1400	12	12	25
3	80	15	15	16

Среднее число дней временной нетрудоспособности в выбороч­ной совокупности определяется по формуле средней арифметической взвешенной:

Средняя из внутригрупповых дисперсий числа дней временной нетрудоспособности по трем цехам завода

Средняя ошибка среднего числа дней нетрудоспособности рас­считывается по формуле для типического бесповторного отбора:

Предельная ошибка выборки определяется с учетом довери­тельной вероятности 0,954:

дн.

Пределы среднего числа дней нетрудоспособности по предпри­ятию в целом

Доля рабочих, не имевших случаев нетрудоспособности, по це­хам предприятия составляет:

Доля рабочих, не имевших случаев нетрудоспособности, по выборке в целом определяется по формуле средней арифметической взвешенной:

Для определения средней ошибки доли рассчитаем среднюю из внутригрупповых дисперсий:

Средняя ошибка доли рабочих, не имевших случаев нетрудоспособности:

Предельная ошибка доли рабочих, не имевших нетрудоспособности:

Пределы доли рабочих, не имевших случаев нетрудоспособности, по предприятию в целом

Пример. На склад завода поступило 100 ящиков готовых изделий по 80 шт. в каждом. Для установления среднего веса деталей проведена серийная выборка. Выборочные средние по сериям составили 16; 15,5; 15 и 15,9 г. Доля бракованных деталей по сериям составила 5; б; 4иЗ% соответственно. С вероятностью 0,954 определите средний вес деталей и долю бракованных деталей в партии.

Средний вес деталей в выборке определяется по формуле средней арифметической простой:

Межгрупповая (межсерийная) дисперсия веса деталей в выборке

Средняя ошибка среднего веса деталей определяется по формуле для серийного бесповторного отбора:

Предельная ошибка среднего веса деталей

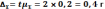
Пределы среднего веса деталей в партии

Доля бракованных деталей в выборке

Межгрупповая (межсерийная) дисперсия доли бракованных деталей

Средняя ошибка доли бракованных деталей

Предельная ошибка доли бракованных изделий

Пределы доли бракованных деталей в партии
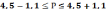