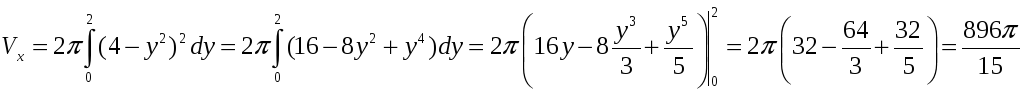- •1. Формула Ньютона-Лейбница.
- •1. Теорема о среднем для определённого интеграла.
- •1. Определение интеграла Римана.
- •1. Теорема о среднем для определённого интеграла.
- •Билет №1
- •1. Формула интегрирования по частям для определённого интеграла.
- •2. Признак сравнения для ряда с неотрицательными членами.
- •3. Признак Лейбница сходимости знакочередующегося ряда.
- •Билет №2
- •1. Теорема о среднем для определённого интеграла.
- •2. Формула замены переменной в определённом интеграле.
- •3. Интегральный признак сходимости числового ряда
- •Билет №3
- •1. Критериий Коши сходимости числового ряда.
- •2. Признак Даламбера.
- •3. Формула Ньютона-Лейбница.
- •Билет №4
- •1. Определение первообразной и неопределённого интеграла.
- •2. Подстановки Эйлера.
- •3. Формула интегрирования по частям для неопределённого интеграла.
- •Билет №5
- •1. Определение первообразной и неопределенного интеграла.
- •2. Интегрирование рациональной функции.
- •3. Обьём тела вращения.
- •Билет №6
- •1. Формула Ньютона-Лейбница.
- •2. Схема исследования функции.
- •3. Первообразная и неопределенный интеграл.
- •Билет №7
- •1. Теорема о среднем для определённого интеграла.
- •2. Понятие суммы ряда. Необходимое условие сходимости.
- •3. Определение интеграла Римана.
- •Билет №8
- •1. Понятие длины кривой. Достаточное условие спрямляемости кривой.
- •2. Формула интегрирования по частям для определенного интеграла.
- •3 Определение обьёма тела.
- •Билет №9
- •1. Определение интеграла Римана.
- •3. Площадь криволинейной трапеции и криволинейного сектора.
- •Билет №10
- •1. Определение первообразной и неопределённого интеграла. Вычисление интегралов
- •2. Формула замены переменной в неопределённом интеграле.
- •3. Интегралы от рациональной функции от sin X и cos X. Методы вычисления.
- •Билет №11
- •1. Теорема о среднем для определённого интеграла.
- •2. Формула замены переменной в определенном интеграле.
- •3. Подстановки Эйлера.
Билет №8
1. Понятие длины кривой. Достаточное условие спрямляемости кривой.
Длина кривой (или, что-то же, длина дуги кривой) в метрическом пространстве — числовая характеристика протяжённости этой кривой. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой существует и конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая.
Для евклидова пространства длина отрезка
кривой определяется как точная верхняя
грань длин вписанных в кривую ломаных.
Для наглядности рассмотрим трёхмерное
пространство. Пусть непрерывная кривая
γ задана параметрически:, ![]() (1)
(1)
где
![]() .
Рассмотрим всевозможные разбиения
интервала параметра [a,b] на m
отрезков:
.
Рассмотрим всевозможные разбиения
интервала параметра [a,b] на m
отрезков:
![]() .
Соединив точки кривой
.
Соединив точки кривой
![]() отрезками прямых, мы получим ломаную
линию. Тогда длина отрезка кривой
определяется как точная верхняя грань
суммарных длин всех таких ломаных.
отрезками прямых, мы получим ломаную
линию. Тогда длина отрезка кривой
определяется как точная верхняя грань
суммарных длин всех таких ломаных.
Всякая непрерывная кривая имеет длину,
конечную или бесконечную. Если все
функции в (1) являются функциями
ограниченной вариации, то длина кривой
существует и конечна. В математическом
анализе выводится формула для вычисления
длины s отрезка кривой, заданной
уравнениями (1), при условии, что все три
функции непрерывно дифференцируемы:
![]() (2)
(2)
Формула подразумевает, что
![]() и длина отсчитывается в сторону
возрастания параметра t. Если
рассматриваются два разных направления
отсчёта длины от точки кривой, то часто
удобно приписать дуге на одном из этих
направлений знак минус.
и длина отсчитывается в сторону
возрастания параметра t. Если
рассматриваются два разных направления
отсчёта длины от точки кривой, то часто
удобно приписать дуге на одном из этих
направлений знак минус.
В n-мерном случае вместо (2) имеем аналогичную формулу:
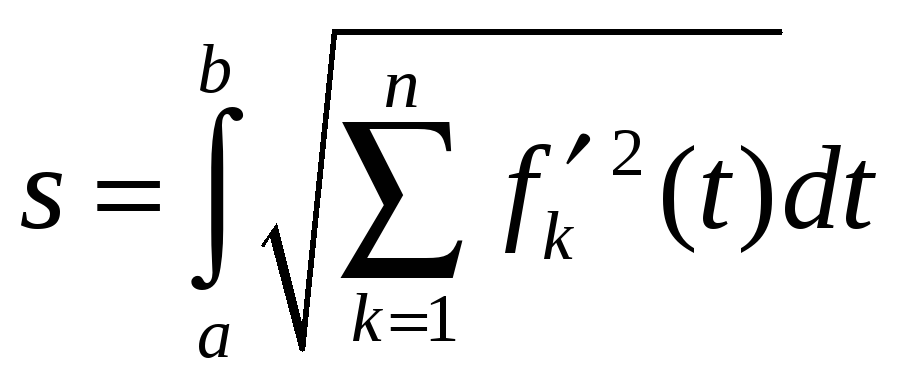
2. Формула интегрирования по частям для определенного интеграла.
Интегрирование по частям — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция представима в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
Для неопределенного интеграла:
![]()
Для определенного интеграла:
![]()
Предполагается, что нахождение интеграла
![]() проще,
чем
проще,
чем
![]() .
В противном случае применение метода
не оправданно.
.
В противном случае применение метода
не оправданно.
Получение формул (для определенного интеграла):
![]()
![]()
![]()
3 Определение обьёма тела.
Понятие объема в пространстве вводится аналогично понятию площади для фигур на плоскости.
Тело называется простым, если его можно разбить на конечное число треугольных пирамид.
В частности, любой выпуклый многогранник является простым телом.
Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами:
-
равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется;
-
если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей;
-
за единицу объема принят объем куба, ребро которого равно единице длины;
Пусть криволинейная трапеция D c границей
![]() вращается вокруг оси ОХ. Поперечными
сечениями являются круги с радиусами
у(х), поэтому
вращается вокруг оси ОХ. Поперечными
сечениями являются круги с радиусами
у(х), поэтому
![]() и
и
![]()
Пусть криволинейная трапеция D с границей
![]() вращается вокруг оси OY, тогда
вращается вокруг оси OY, тогда
![]() и
и
![]()
Пример:
Определить объем тела, образованного
вращением фигуры D с границей
![]()
а) вокруг оси ОХ;
б) вокруг оси OY.
При вращении фигуры D вокруг оси ОХ
получим параболоид (рис а), объем которого
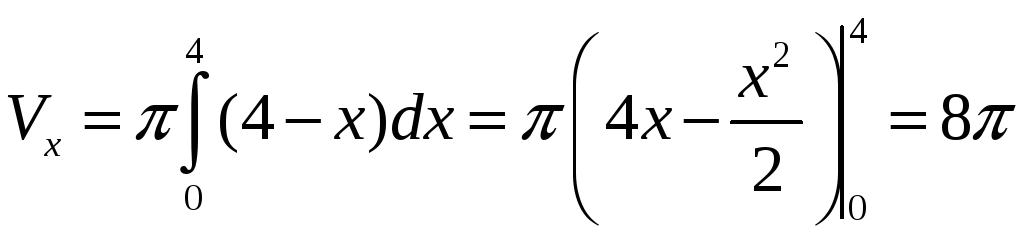

При вращении фигуры D вокруг оси OY получаем тело, изображенное на рис. б. Его объем