2. Подстановки Эйлера.

Подстановки, служащие для приведения интегралов вида , где

R (x, y) — рациональная функция от х и у, к интегралам от рациональных функций. Предложены Эйлером в 1768.

Первая Эйлерова подстановка применима, если а>0;

Вторая Эйлерова подстановка применима, если с > 0;

Третья Эйлерова подстановка где λ — один из корней трёхчлена , применима, если корни этого трёхчлена действительны. На практике Э. п. требуют громоздких преобразований и потому вместо них обычно пользуются теми или иными искусственными приёмами, упрощающими вычисление.

Аналогичные подстановки делаются в теории чисел при решении неопределённых уравнений 2-й степени в рациональных числах.

3. Формула интегрирования по частям для неопределённого интеграла.

Интегрирование по частям — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция представима в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

Для неопределенного интеграла:

Для определенного интеграла:

Предполагается, что нахождение интеграла проще, чем . В противном случае применение метода не оправданно.

Получение формул (для определенного интеграла):

Билет №5

1. Определение первообразной и неопределенного интеграла.

Первообразная:

Функция F(x) называется первообразной для функции f (x) на данном промежутке, если для любого х из данного промежутка F'(x)= f (x).

Основное свойство первообразных:

Если F(x) – первообразная функции f(x), то и функция F(x)+ C , где C –произвольная постоянная, также является первообразной функции f(x) (т.е. все первообразные функции f(x) записываются в виде F(x) + С ).

Геометрическая интерпретация:

Графики всех первообразных данной функции f(x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.

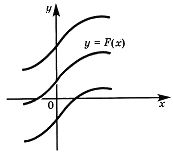
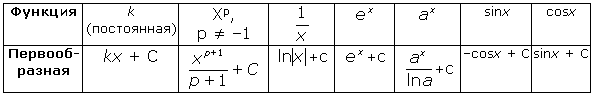
Первообразная - это величина, обратная производной. Т.е. если мы знаем, что , то для первообразной будет . Еще первообразная связана с определенным интегралами формулой Ньютона-Лейбница. Т.е. по сути первообразная есть интеграл, геометрический смысл которого - площадь под кривой.

Производная от функции скорости есть ускорение (быстрота изменеия скорости), а первообразная от функции скорости характеризует пройденное расстояние при данной скорости.

Правила нахождения первообразных:

Пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x). Тогда:

1. F( x ) ± G( x ) – первообразная для f(x) ± g(x);

2. аF( x ) – первообразная для а f(x);

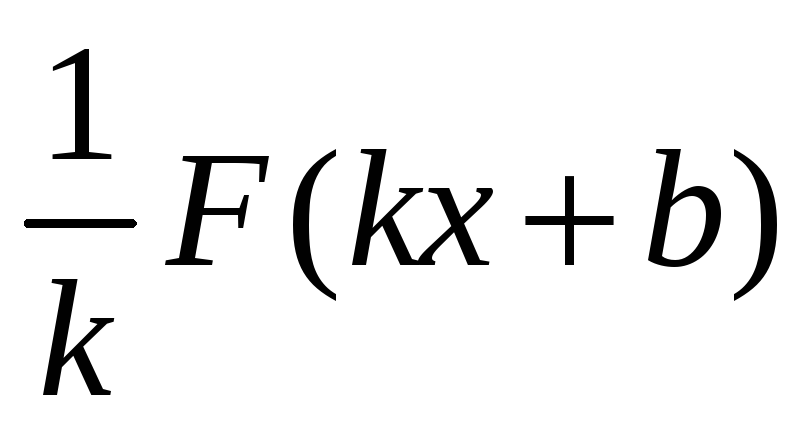3. – первообразная для а f( kx + b ).

Примеры.

1. Выяснить, является ли функция первообразной для функции .

Решение: , т.е. F'(x) = f(x), следовательно, F(x)является первообразной для функции f(x).

Неопределенный интеграл:

Неопределенный интеграл данного выражения или данной функции называется наиболее общий вид его первообразной функции. Обозначается он . Постоянное слагаемое подразумевается включенным в это обозначение. Слово «неопределенный» подчеркивает, что в общее выражение первообразной функции входит постоянное слагаемое, которое можно взять по произволу.

Выражение называется подинтегральным выражением, а - подинтегральной функцией, переменная x – переменная интегрирования.

Более точное определение -

Пример:

;

;

Геометрический смысл неопределенного интеграла следует из геометрического смысла производной: уравнение y=F(x) +С на плоскости ХОY определяет семейство кривых (называемых интегральными кривыми), для которых в точке с абсциссой х угловой коэффициент касательных равен )

Физический смысл неопределенного интеграла: т.е. интеграл от скорости неравномерного прямолинейного движения дает зависимость пути от времени .

Свойства неопределенного интеграла:

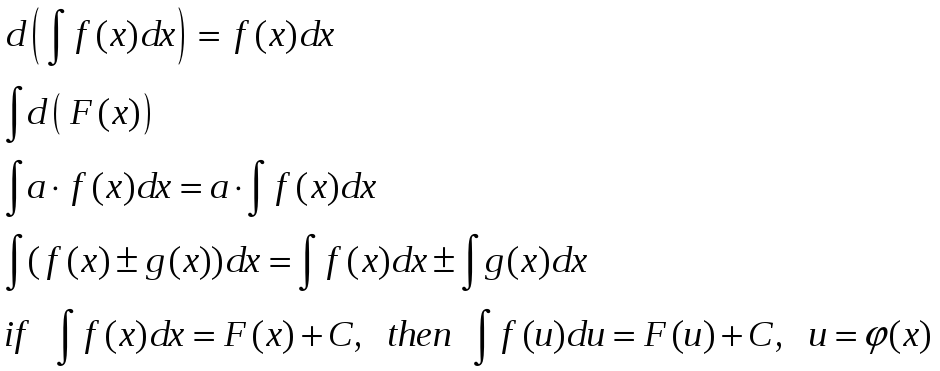
Основные методы интегрирования:

5. Метод внедрения нового аргумента:

Если , то , где - непрерывно дифференцируемая функция

6. Метод разложения:

Если , то

7. Метод подстановки:

Если - непрерывна, то полагая , где непрерывна вместе со своей производной , получим

8. Метод интегрирования по частям:

Если u и v – некоторые дифференцируемые функции от x, то